Analysis of Ancient and Modern Guitars
Article Information
Giuseppe Cuzzucoli *
Via Levante, 6, 10044 Pianezza (TO), Italy
*Corresponding Author: Giuseppe Cuzzucoli, Via Levante, 6, 10044 Pianezza (TO), Italy
Received: 03 March 2020; Accepted: 09 April 2020; Published: 13 May 2020
Citation: Giuseppe Cuzzucoli, Analysis of ancient and modern guitars. Journal of Analytical Techniques and Research 2 (2020): 44-69.
View / Download Pdf Share at FacebookAbstract
This article reports the results of an investigation performed on the Gottlob Schuster guitar made available by the owner (Marco Bazzotti). The purpose of this investigation is twofold: at first to demonstrate how a limited number of key parameters can proficiently be used to assess an existing instrument, eventually to replicate its sounding characteristic; secondly to gain an understanding of the design criteria that guided a luthier in designing an instrument of its production, and how certain criteria (and the underlying physical and geometrical parameters) evolved in the course of the years. The features and performances of the Gottlob Schuster guitar have been compared with the features of some other ancient and modern instruments:
1. A replica of the Torres guitar with cardboard back and sides (1862) by Luthier Zontini.
2. A Fleta guitar, 1921 (considered the first built by this Luthier).
3. A Simplicio guitar, 1931 (the last production period of this Luthier).
4. A Gallinotti guitar, 1974 (the latest period of production).
5. A Josè Ramirez guitar, 1970.
6. A Garrone guitar, 2011.
nvestigation articles nvestigation Research articles nvestigation review articles nvestigation PubMed articles nvestigation PubMed Central articles nvestigation 2023 articles nvestigation 2024 articles nvestigation Scopus articles nvestigation impact factor journals nvestigation Scopus journals nvestigation PubMed journals nvestigation medical journals nvestigation free journals nvestigation best journals nvestigation top journals nvestigation free medical journals nvestigation famous journals nvestigation Google Scholar indexed journals Gottlob Schuster guitar articles Gottlob Schuster guitar Research articles Gottlob Schuster guitar review articles Gottlob Schuster guitar PubMed articles Gottlob Schuster guitar PubMed Central articles Gottlob Schuster guitar 2023 articles Gottlob Schuster guitar 2024 articles Gottlob Schuster guitar Scopus articles Gottlob Schuster guitar impact factor journals Gottlob Schuster guitar Scopus journals Gottlob Schuster guitar PubMed journals Gottlob Schuster guitar medical journals Gottlob Schuster guitar free journals Gottlob Schuster guitar best journals Gottlob Schuster guitar top journals Gottlob Schuster guitar free medical journals Gottlob Schuster guitar famous journals Gottlob Schuster guitar Google Scholar indexed journals geometrical parameters articles geometrical parameters Research articles geometrical parameters review articles geometrical parameters PubMed articles geometrical parameters PubMed Central articles geometrical parameters 2023 articles geometrical parameters 2024 articles geometrical parameters Scopus articles geometrical parameters impact factor journals geometrical parameters Scopus journals geometrical parameters PubMed journals geometrical parameters medical journals geometrical parameters free journals geometrical parameters best journals geometrical parameters top journals geometrical parameters free medical journals geometrical parameters famous journals geometrical parameters Google Scholar indexed journals key parameters articles key parameters Research articles key parameters review articles key parameters PubMed articles key parameters PubMed Central articles key parameters 2023 articles key parameters 2024 articles key parameters Scopus articles key parameters impact factor journals key parameters Scopus journals key parameters PubMed journals key parameters medical journals key parameters free journals key parameters best journals key parameters top journals key parameters free medical journals key parameters famous journals key parameters Google Scholar indexed journals acoustical behavior articles acoustical behavior Research articles acoustical behavior review articles acoustical behavior PubMed articles acoustical behavior PubMed Central articles acoustical behavior 2023 articles acoustical behavior 2024 articles acoustical behavior Scopus articles acoustical behavior impact factor journals acoustical behavior Scopus journals acoustical behavior PubMed journals acoustical behavior medical journals acoustical behavior free journals acoustical behavior best journals acoustical behavior top journals acoustical behavior free medical journals acoustical behavior famous journals acoustical behavior Google Scholar indexed journals analysis articles analysis Research articles analysis review articles analysis PubMed articles analysis PubMed Central articles analysis 2023 articles analysis 2024 articles analysis Scopus articles analysis impact factor journals analysis Scopus journals analysis PubMed journals analysis medical journals analysis free journals analysis best journals analysis top journals analysis free medical journals analysis famous journals analysis Google Scholar indexed journals instruments articles instruments Research articles instruments review articles instruments PubMed articles instruments PubMed Central articles instruments 2023 articles instruments 2024 articles instruments Scopus articles instruments impact factor journals instruments Scopus journals instruments PubMed journals instruments medical journals instruments free journals instruments best journals instruments top journals instruments free medical journals instruments famous journals instruments Google Scholar indexed journals objective articles objective Research articles objective review articles objective PubMed articles objective PubMed Central articles objective 2023 articles objective 2024 articles objective Scopus articles objective impact factor journals objective Scopus journals objective PubMed journals objective medical journals objective free journals objective best journals objective top journals objective free medical journals objective famous journals objective Google Scholar indexed journals physical parameters articles physical parameters Research articles physical parameters review articles physical parameters PubMed articles physical parameters PubMed Central articles physical parameters 2023 articles physical parameters 2024 articles physical parameters Scopus articles physical parameters impact factor journals physical parameters Scopus journals physical parameters PubMed journals physical parameters medical journals physical parameters free journals physical parameters best journals physical parameters top journals physical parameters free medical journals physical parameters famous journals physical parameters Google Scholar indexed journals proficiently articles proficiently Research articles proficiently review articles proficiently PubMed articles proficiently PubMed Central articles proficiently 2023 articles proficiently 2024 articles proficiently Scopus articles proficiently impact factor journals proficiently Scopus journals proficiently PubMed journals proficiently medical journals proficiently free journals proficiently best journals proficiently top journals proficiently free medical journals proficiently famous journals proficiently Google Scholar indexed journals
Article Details
The main reference for this text is the book ‘La Progettazione della Chitarra Classica’ (Cuzzucoli e Garrone- Create Space Independent Publishing, 2014) or its English translation ‘Classical Guitar Design’ (Springer, 2019), where the acoustical behavior of the classical guitar is discussed, together with an explanation of the main parameters mentioned in the text. A description of the measurement method and the hardware and software tools is in line with the method presented in the above mentioned book, and will only summarized briefly hereafter. Finally a table summarizes the feature of the above mentioned instruments, and the relevant results of the analysis.
1. The Instrument and its Geometric Dimensions
The definition of 'ancient' instruments compared to 'modern' instruments is certainly approximate and questionable. What is not disputable is that the way of conceiving the guitar as a whole (structure, executive practice and more) has evolved over the past two centuries. Basing on the analysis method that will be exposed, the comparison between the few instruments here considered shows that some evolutionary lines in the design of the instruments can be identified. At the same time it becomes possible to fix some ideas on the design criteria which guided the luthiers in building their instruments, as well as on the 'objective' performance of ancient instruments compared to the performance of modern instruments. The instrument we analyze was built by the luthier Carl Gottlob Schuster, active in Markneukirchen (Austria) at the end of the 19th century and best known for his production of renowned bowed instruments. The instrument (Figure 1) carries the label «Carl Gottlob Schuster jun. ~1900, Markneukirchen, Gegründet 1824». The instrument, actually in good playing conditions, can be considered a 'transition' guitar: typical features of the modern guitar (the raised fretboard, the modern-style bridge..) are accompanied by some 19th century guitar features (small body, wide lower bout, limited volume of the air in the body...).

Figure 1: The instrument.
The basic geometrical dimensions obtained from measurements on the body of the guitar are:
- Height of the sizes: from 81.5 at the tail block to 80 mm. at the waist; decreases up to 66.5 mm. at the heel, Mean height: 77 mm.
- Estimated table surface 910 cm2.
- Sound hole diameter: 82
- Table thickness at the hole: 3
- Volume of the air in the body: 7
The Helmholtz frequency was evaluated by immobilizing the body walls (table and bottom), exciting the indoor air with a loudspeaker driven by a sinusoidal generator and evaluating (with a sound level meter) the frequency at which the sound pressure radiated through the hole is maximum. The procedure resulted in an Helmholtz frequency FH of 153 Hz.
2. The Measurements Tools: Hardware and Software
In order to gain a good knowledge of the acoustical characteristics of instrument under investigation, I propose a limited set of measurements which can be done even by luthiers using commonly available tools, namely in a non specialized acoustic lab. This set includes
- Excitation of the soundboard at the bridge
- Excitation of the soundboard with closed
- Excitation of the back at the bridge
The discussion on different methods for exciting the vibrating plates in an instrument is beyond the scope of this text. The investigation on this guitar has been performed using the so called impulsive excitation (or acoustic hammer): the table is hit by a special hammer producing a very short force pulse whose amplitude can set the soundboard (or the back) into motion. Mathematically, this input signal contains the spectral components of the force in a wide band of frequencies. The output signal (the sound pressure) acquired by a good quality microphone contains the global response (in terms of sound pressure) of the vibrating surfaces of the instrument (soundboard, back, sound hole) with respect to all the frequencies included in that band. Therefore, a device must be conceived to drive the soundboard with a proper impulsive excitation. (Figure 2) shows the details of a test rig prepared for this purpose, including the hammer, the support of the instrument, the microphone.

Figure 2: The test rig.
The complete guitar is inspected by hanging the whole on a stand with an elastic means, as shown in the (Figure 3). The guitar is suspended from two properly sized elastic bands, this way being able to vibrate free of any damping due to contact points. The acoustic hammer is basically a pendulum oscillating on two ball bearings. On the head that holds the pendulum a little arm is also attached, bearing a sexagesimal Vernier scale that establishes the starting point of the pendulum before percussion. This way the angle is constant, and the percussion on the soundboard yields replicated results. The pendulum is set on the lock and then released, whether manually or, preferably, by an electromagnetic releasing device. The height of the arm that sustains the pendulum must be settled so as to get the percussion in a proper point: for example the bridge saddle or the back in a position corresponding to the bridge. A quality microphone should be used. Its response must be flat up to at least 50 Hz, in order to obtain the lower harmonics of the guitar sound. The microphone is placed at the level of the sound hole, 80 cm. from the soundboard surface, in order to capture the sound emission from both soundboard and sound hole.

Figure 3: The support of the pendulum and the sexagesimal vernier.
The computer software in use was specifically conceived and developed for the analysis of the guitar sound. The program determines the spectral composition of the signal by implementing its Fast Fourier Transform with a resolution of about 0.3 Hz in the frequency band up to 1200 Hz or, with lower resolution, up to 10000 Hz. Within this range of frequencies, both the resonances and antiresonances of the sound are displayed; the algorithm is known as the Fast Fourier Transform. The signal is examined within a limited (and variable) time window, for instance 100 ms. By scrolling the window along the signal timeline we can see the variation of the spectrum over time, hence how the amplitude of the resonances decays during the time. Within the reading window, the acquired data are 'filtered' according to particular algorithms described in the literature, in order to limit the signal band and to cancel spurious data that could lead to misinterpretable results.
Besides the rectangular window, various types of window are selectable. For the purpose of the current study the Hanning window was selected. Besides the resonances, whose frequency, amplitude, and quality factor Q are calculated by the software, various representations of the spectrum are displayed, of which one of the most interesting is the third of octave one. The software associates each band to the average amplitude value of the response in that band, still on a logarithmic scale: the average response in that band assumes an especially important global significance, in that it summarizes the weight of specific resonances within one band or (extending this concept) in more adjoining bands. The response in time domain, namely the evolution of the sound signal during the time shows the attack transient and its duration, affecting the promptness of response and the attack of the sound (its sharpness, or smoothness).
The decay time affects sustain as well as projection. The diagram known as Waterfall chart is a 3D representation of the changes occurring in the signal spectrum over time: the spectrum representations are superimposed (and staggered for clear viewing) forming a sort of ‘solid’ surface, with frequencies displayed on the horizontal axis and values of the single spectral lines, calculated at different moments, displayed on the vertical axis. Not only the position and amplitude of the resonances are important, but also their decay rate, which corresponds to the sound sustain. An excessively rapid damping of certain resonances often implies that some tones die out abruptly. The estimation of the decay can be performed for each of the selected resonances.
3. The Data from Measurements
The processing of the microphone signal (related to the sound pressure) results in a set of diagrams, each of which can be viewed as a different representation of the sound, eventually at different times. The most relevant ones (reported below) are:
- The temporal evolution of the sound signal in a short time scale resulting from the impulse excitation of the
- The graph of the global response of the instrument (in terms of sound pressure) excited on the table at the bridge
- Thirds of octave chart and the amplitude mean values (in log. scale) in registers which are believed to be significant for the quality of the instrument. For example, the value in the range 80 – 8000 Hz is significant for the yield in the band of the fundamentals of the guitar tones.
- The graph known as waterfall
- The decay time diagram, where for each of the resonances selected in the signal spectrum the time constant of the exponentially decaying amplitude (hence the duration) is
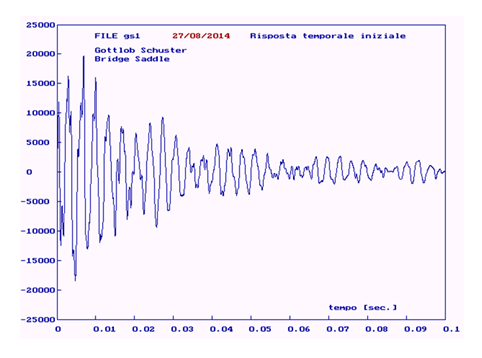
Figure 4: Time response of the sound signal.
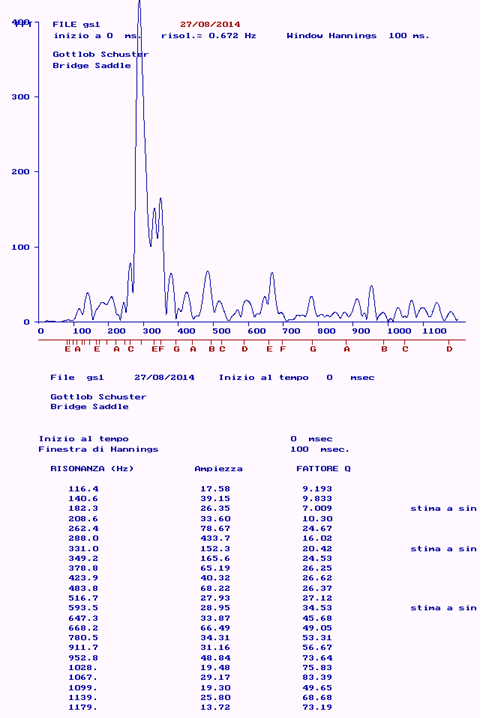
Figure 5: Resonances, antiresonances, associated amplitudes and Q - factors.
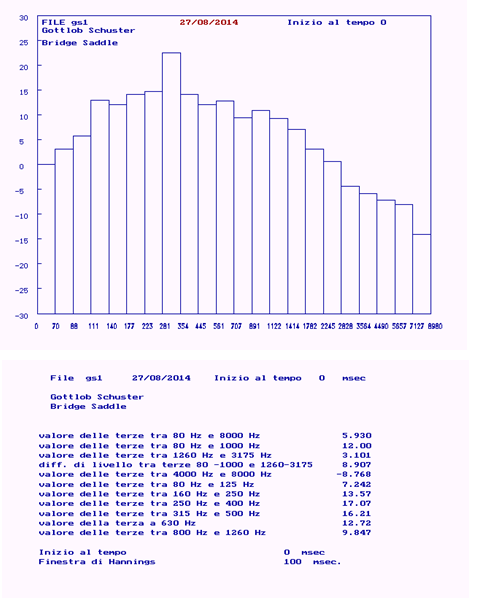
Figure 6: Third of octaves chart, amplitude mean value (log.) in significant registers.
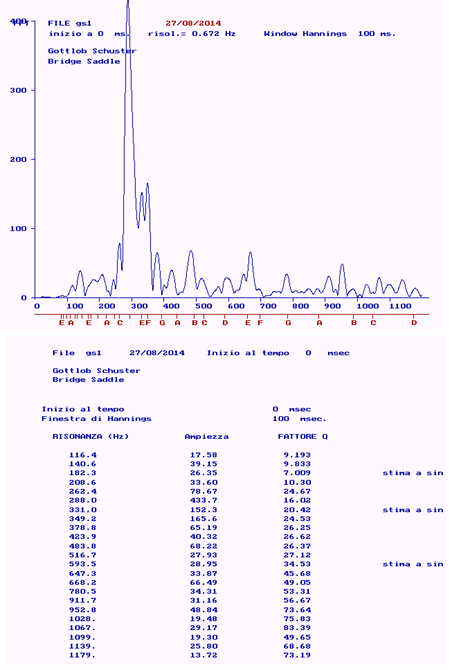
Figure 7: Spectral response and characteristic parameters of the main resonances (soundboard).
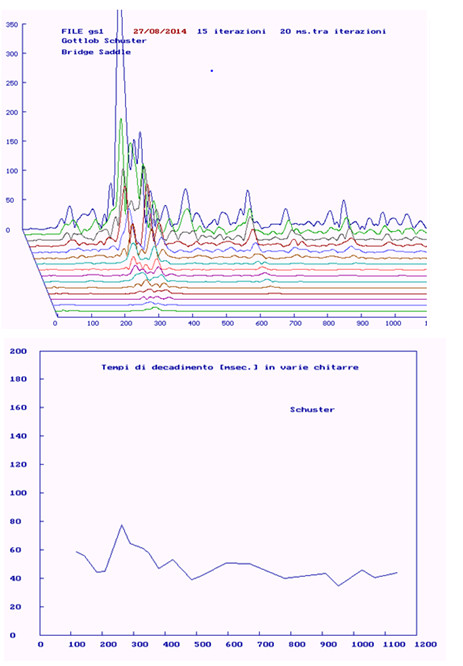
Figure 8: The waterfall chart (right) and the decay times at the selected resonances.
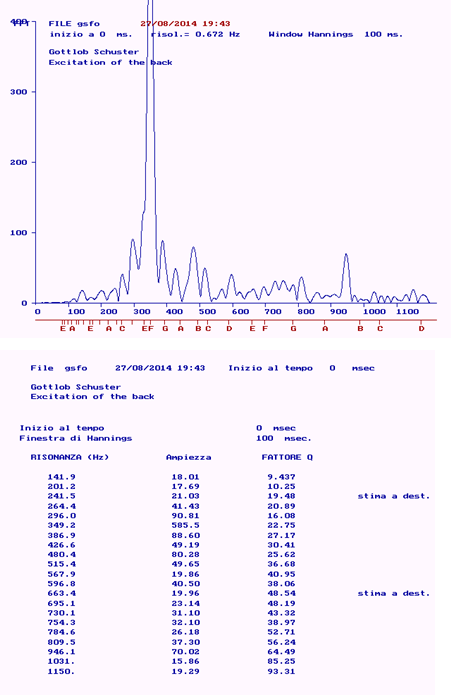
Figure 9: Spectral response and characteristic parameters of the main resonances (back).
4. Parameters Estimation
The data collected from the above charts must be interpreted in order to obtain the significant physical parameters specific for each individual instrument. A physical model of the resonator, namely a depiction of its basic components and their interaction, serve this purpose. We have developed a three-degree of freedom model where the fundamental resonator components (soundboard, back, Helmholtz resonator) are represented to highlight both their physical structure and their interaction. Back and soundboard are represented as simple oscillators featuring mass, stiffness and losses, while the sound hole is shaped like a piston defined by its air, mass and radiation resistance that, along with the elasticity of the air in the body and the rigid sides, define the Helmholtz resonator. The values of the oscillators physical parameters and, coherently with the test results, the sound pressure from the oscillating surfaces, are the outcomes from the model to an external force excitation. Even if simplified (in that the phenomena involved in the resonator are reduced to vibrations of simple oscillators) and partial (in that it represents the physical behavior of the instruments in the low – mid range of frequencies), the model is a whole which involves a mathematical formulation relating acoustical parameters (mass, stiffness, loss factors, vibrating surfaces) generally not measurable to objective and measurable quantities (frequencies, amplitudes, Q-factors, vibration modes). To identify the acoustical parameters often is necessary to alter the standard geometry of the instrument body and to include the results from this ‘anomalous’ situation in the list of the standard inputs. Therefore we measured also the resonances after covering the sound hole and after loading the top with a known mass. Even if the model can handle the loss-related parameters of the resonator, for the current analysis we will neglect this subject.
The input data, collected from the above charts are
4.1 Basic resonances
|
F1 (Resonance of the air) |
140.6 Hz |
|
FH (Helmholtz Resonance) |
153 Hz |
|
F2 (Soundboard basic resonance) |
276 Hz |
|
F3 (Soundboard Resonance due to the first mode of the back) |
314 Hz |
|
Fbc (Covered sound hole resonance) |
65.9 Hz |
|
Fbcm (Covered sound hole resonance with additional mass) |
235.6 Hz |
4.2 Resonances due to the higher modes of the back
|
F4, F5 (Soundboard resonances due to the second mode of the back) |
287, 348 Hz |
|
F6, F7 (Soundboard resonances due to the third mode of the back) |
288, 404 Hz |
The acoustical parameters estimated by the model are
|
F1r (Rigid body air resonance) |
142 Hz |
|
F2r (Rigid body soundboard resonance) |
290 Hz |
|
Ft0 (Natural frequency of the soundboard) |
263 Hz |
|
FB1 (First mode of the back) |
294 Hz |
|
FB2 (Second mode of the back) |
336 Hz |
|
FB3 (Third mode of the back) |
398 Hz |
|
Vibrating mass (soundboard) |
73 gr |
|
Vibrating surface (soundboard) |
360 cm2 |
|
Stiffness (soundboard) |
203000 N/m |
|
Surface/mass ratio |
4.93 |
|
Coupling coefficient soundboard to air |
0.789 |
|
Coupling coefficient back to air (first mode) |
0.67 |
|
Coupling coefficient back to air (second mode) |
0.61 |
|
Coupling coefficient back to air (third mode) |
0.59 |
5. The Development of the Guitar through its Mechanical / Acoustical Parameters
The development of the guitar during the past two centuries did not follow a linear path. The historical luthiers tried to optimize the sound of their instruments by following different and sometimes contradictory trends; their effort was to optimize the body of the instrument and the geometry of the table (the 'project' of the instrument) with the target of creating a new sound satisfying the needs of musical forms in turn 'new'.
In the early decades of the twentieth century a new way of designing the guitar begins to stand out, which characterizes the most of the ‘modern’ instrument (naturally without prejudice to the concept that every manufacturer, while remaining in the scope of this model, has its own specificity). The 'ancient' guitar and the ' modern ' one coexisted until the 1930s-40s of the twentieth century, when the only survived model is the one we recognize today. This evolution is reflected in a number of acoustical and mechanical characteristics which evolved in parallel to the increasing demands required to the instrument. Next (Table 1). Reports the most significant parameters measured on a limited number guitars, each of which being in some way representative of a certain moment of this evolution. In particular:
|
Instrument |
Helmholtz resonance [Hz] |
Body volume [lt.] |
|
Guadagnini(1821) |
176 |
7 |
|
Guadagnini style Italian guitar (ca. 1850) |
176 |
7 |
|
Lacôte style guitar (ca.1870) |
174 |
8 |
|
Zontini-Torres guitar (original 1862) |
143 |
11 |
|
Gottlob Schuster guitar (early 1900s) |
153 |
7 |
|
Italian parlor guitar (early 1900s) |
140 |
11 |
|
Fleta (1921) |
143 |
12 |
|
Simplicio (1931) |
129 |
14 |
|
Pignat Torres style (1956) |
141 |
11 |
|
Gallinotti (1974) |
129 |
14 |
|
Estudiantina (1960) |
141 |
12 |
|
Suzuky (1970) |
127 |
13.5 |
|
Josè Ramirez (1970) |
121 |
16 |
|
Kohno (1985) |
127 |
14 |
|
Novelli (1994) |
130 |
13.5 |
|
Garrone (2011) |
129 |
14 |
5.1 Body volume and Helmholtz resonance
The development of the shape of the guitar in the nineteenth and twentieth centuries is characterized primarily by a progressive increase in the volume of air in the body, different diameters of the sound hole and different thicknesses of the soundboard at the hole. This last parameter is a sort of virtual channel along which the air flows from the inside of the body towards the outside and vice versa. The evolution is reflected in the value of the Helmholtz resonance and body volume measured in a number of ancient and modern instruments, covering an historical period which ranges from the first decades of the 19th century until today. (Table 2) shows these values.
Table 1: Resonator parameters estimated in several guitars.
This table highlights the tendency, during the evolution of the instrument, to lower the tuning note by reducing the Helmholtz resonance, as well as the attempt to increase the loudness of the sound by increasing the size of the body and - consequently - the effective vibrating surface of the table. In ancient instruments (where the height of the sides was limited and the volume of air in the body was low), the Helmholtz resonance was positioned at about 175 Hz (see the Guadagnini guitar). The model which inspired Guadagnini achieved considerable popularity and was in production - at least in Italy – up to the 1930s, for example in Gallinotti, Mozzani and others, and was characterized by wide bouts and eight-shaped body. The low body volume and high Helmholtz resonance, though with a different shape, was a characteristic of the ‘French’ school (Lacôte, Grobert and others), and this model too survived up to the early 1900s.
In parallel (and not as an alternative), a new model of the instrument is developed, designed around a greater body volume and a different table bracing, where the Helmholtz frequency FH drops to about 150-140 Hz; the immediate consequence is an increase in the body volume, which grows from (typically) 7 up to 12 liters. This clearly indicates the tendency to move the tuning note down, to enhance the response of the instrument in the register interested by the lower tones of the guitar scale. The instruments from Torres and followers achieved remarkable consistency in the second half of the 1800s, becoming the immediate precursors of the modern classical guitar. The table shows a few example of some instruments belonging to this typology: first the Zontini - Torres guitar, but also the Gottlob Schuster and the first Fleta guitar of 1921. This ‘medium sized’ typology coexisted with the instruments of the previous typology (like the 'Guadagnini' or the 'French school' models) and was produced well up the 1960s with small variation in the Torres original soundboard bracing; the Italian guitar from Pignat (1956) is an example.
The Torres fan-braced Spanish guitar led to an instrument typology which achieved a large popularity from the last decades of the 19th century. This model is characterized by a decidedly greater body volume; the volume increases up to about 14 liters while the Helmholtz frequency FH drops to around 130 Hz. The Simplicio guitar examined is an example, although probably other luthiers before Simplicio and after Torres (like the Ramirez or Garcia) had used this form. This model of the classical guitar is currently in production today and the only one to which the luthiers currently adhere, albeit with the obvious individual customizations.
5.2 Significant resonance frequencies
The volume of the body, which is one of the factors influencing the Helmholtz's resonance (not the only one but the one on which luthiers have instinctively worked more often), is not enough to characterize the evolution of the instrument alone. Indeed the shape and volume of the body are in some way elements to be exploited to realize a certain idea of the peculiar sound of each guitar maker. Certainly the artisans who built stringed instruments (violins, lutes, mandolins, guitars or others) were conscious that the final quality of an instrument is related to how the table closing the body is built. And then they endeavored to 'feel' by ear the response of a table, and secondly tried to devise specific construction systems, aimed to obtain the ‘expected performance’, namely the concept of sound they were demanding from their instruments. In the past this process was more or less empirical; today we got a deeper knowledge of the relationship between the performance of an instrument and the acoustical characteristics of its components, also supported by new tools which can assist the traditional construction techniques.
Whatever design criteria are adopted, once the soundboard and the back are glued to the sides (and therefore become part of the resonator), its behavior is conditioned, at least in the low to mid-range of tones, by some specific basic resonances, namely that of the air F1 (the ‘tuning note') and those of the table F2 and the back F3. In turn these resonances are determined by the natural frequency of the soundboard Ft0 and the back Fb0 and by their coupling with the air in the body. Looking to Ft0 and Fb0 as natural frequencies of simple oscillators, they are related to the ratio of their own effective stiffness times vibrating mass. The comparison between several guitars (Table 1.) highlights that the orientations and choices of their builders were very different, and mirrored in different values of the most significant acoustical parameters, as reported in (Table 3).
Table 3: Main resonances estimated in several guitars.
5.3 Decay time in resonance
The position of both the Helmholtz frequency and the basic resonances, are not enough to characterize the behavior of the instrument, not even in the middle-low register dominated by the basic resonances. Both the instrument soundboard and back, as well as the air in the body, are elastic systems, therefore their motion progresses because of the cumulated energy even when the external excitation has ceased. From a general point of view, the fact that the oscillatory system - once put into vibration - continues to oscillate, is related to his inertia, while the fact that the oscillation decays more or less rapidly is related to the losses to which the vibrating elements are subjected in their motion: mainly the losses due to viscous friction within the vibrating masses (the wood of the boards) and the radiation losses which the vibrating surfaces undergo when moving in the surrounding air. Another phenomenon that conditions the more or less rapid damping of the oscillation amplitude (i.e. the decay time) is related to how quickly the oscillator is able to absorb (use and dissipate) the energy applied to it. Ideally in resonance the impedance of an oscillator is ideally zero and the velocity is ideally infinite. In the real world the impedance is not null, and the gain is not infinite due to the losses. Because of the not null impedance in resonance, if a signal applied to of an oscillatory system has a spectral component that coincides with the resonance frequency of the oscillator, that component is absorbed (and eventually used) quickly from the oscillator. The consequence is that the oscillation amplitude decays more or less rapidly depending on the physical characteristics of the oscillator under resonance conditions.
This mechanism is summarized by the quality coefficient (Q - factor), which can be formulated mathematically to evidence its connection with the physical parameters (stiffness, mass, loss coefficient) of the oscillator. (Figure 5) reports the Q – factors evaluated at the resonances in the Gottlob Schuster guitar. Having revised the physical reasons that influence the decay time, the effects on the sound of a guitar are now to be examined.
- The first basic resonance F1 (the tuning note) is excited by tones even far from its frequency. In this sense the luthiers are used to call it the 'base note' and to measure it by ear attempting to reach a target value. Its presence in the sound recipe gives a basic coloring sound to the instrument timbre. If the decay time is high (and therefore the base note has a high sustain) this coloring lasts a long time and strongly contributes to the sound texture of the instrument. If vice versa the decay is fast, the timbre is 'nasal' and the sound quality is From these considerations one can argue that a high value of the decay time at the air resonance is a feature of best instruments
- Similar considerations apply to the second basic resonance F2 which decays more rapidly than the first. This is because the elastic characteristics of the wood are very different from those of the air. The Q - factor of the soundboard resonance is generally higher than for air, meaning that this resonance uses and dissipates more rapidly the energy from the vibrating
- Another effect (especially important at higher frequencies) is due to the absorption of the vibratory energy that occurs near certain resonances; this absorption causes a rapid decay of sound, linked both to the physical characteristics of a particular mode of vibration and to the characteristic impedance of the
The decay time is the time constant of the exponentially decaying amplitude of the sound signal. It depends on the effective vibrating mass, on the losses due to viscous friction in the wood and on the exchange of energy between soundboard, back and air, therefore their coupling. Finally, it depends not only from the wood characteristics (losses), but basically from the design of soundboard and back (size, bracing) and their coupling to the air resonances.
|
Guitar |
Air resonance |
Soundboard resonance |
||||
|
Frequency [Hz] |
Decay time (ms) |
Selectivity |
Frequency [Hz] |
Decay time (ms) |
Selectivity |
|
|
Zontini -Torres |
84.5 |
85.46 |
21.86 |
181.6 |
66. 6 |
38.0 |
|
Gottlob Schuster |
140.6 |
58.21 |
21:29 |
285 |
64.4 |
58.26 |
|
Fleta (1921) |
115 |
91.09 |
32.93 |
230 |
5 6 |
40.2 |
|
Simplicio (1931) |
96 |
161.8 |
48.24 |
192.4 |
40.7 |
24.63 |
|
Gallinotti (1974) |
104 |
144.6 |
47.38 |
221 |
47. 6 |
32.99 |
|
Garrone (2011) |
95 |
208.7 |
62.22 |
200 |
87.2 |
54.75 |
By measuring the time constant at the main resonances in a guitar under test and plotting it as a function of the frequency, a chart is obtained like the one in (Figure 8) (left) for the Gottlob Schuster guitar. The delay times at the basic resonances for the guitars under investigation are given in (Table 4)., while (Figure 10) allows comparing the decay times for these instruments at all their significant resonances (and not only at the basic ones), in order to find some time evolution in the design criteria of their manufacturers as well as some correlation with their sounding features.
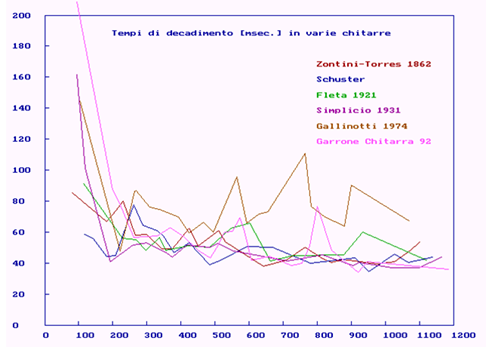
Figure 10: Decay time in several guitars.
The chart evidences that the decay time at the air resonance 'historically' tends to grow from the ancient guitars to the modern ones. An exception is the Gallinotti guitar where the decay time at the first resonance (the tuning note) is slightly lower than in the two other modern guitars, the Simplicio and the Garrone. This guitar deserves a special attention regarding this aspect: even if the decay time at air resonance is slightly lower than in the Simplicio or in the Garrone, in this instrument the decay time is pronounced and pointed at certain significant resonances: at 268 Hz (corresponding to the second mode of the backboard), at 594, 763, 900 Hz (corresponding to the air to soundboard mode coupling at frequencies higher than the Helmholtz frequency).
As a consequence, in the Gallinotti guitar the sustain is slightly lower at the tuning note but, at the same time, in resonance the sound is maintained up to 900 Hz, what can explain the features of this instrument (a soft sound in the low registers but well present in the mid to high registers). In this instrument the projection (i.e. the combination of sound loudness and sustain) is very effective and give it a precise personality. The Simplicio guitar proves to be the first 'modern' guitar. The sound persistence at the air resonance is decidedly higher than in the previous 'ancient' guitars. However, beyond the air frequency the decay times (i.e. the tones persistence) at the highest frequencies is scarce: no frequency emerges significantly and the graph is quite flat. In the sounding features of such an instrument the tuning note can be expected to give a dominant and long lasting coloring to the sound texture, while the other dominants in the sound dies quickly away.
In the Garrone guitar the air resonance has an exceptionally high persistence compared to other instruments under tests, and that gives a dominant character to the sound texture. The decay time is relevant in some of the resonance frequencies, namely 368, 572, 800 Hz. These resonances typically are associated to the air-to-soundboard mode coupling at frequencies higher than the Helmholtz frequency. On the contrary, comparing the three ancient and the three modern guitars it comes into evidence from Fig. 10 that in the first group the decay time at the air resonance is significant lower, while is similar or even greater at the second (soundboard) resonance, with the exception of the Garrone guitar where the decay time is very high at both the air and at the table resonances. In the most ancient instruments this behavior is due to the inertia of the soundboard, which was generally more massive; it has an impact on the sound features: in the ancient guitars the tuning note does not predominate in the timber, but both the main resonances contribute to the color of the sound texture. A more clear sound (compared with the modern instruments) can be expected from these guitars. The historical evolution (and - in all likelihood - the musical taste) gradually led to privilege a low and deep instrument tuning, up to the most recent guitars (Garrone 2011) where both resonances persist for a long time with a decisive prevalence of the tuning note. It seems that these considerations on the evolution of the decay times and its impact and on the sound texture can partly mirror the changes over the time in musical taste and in performing practice. The instruments on one side adapted to these changes and on the other side conditioned them.
6. Remarks on the Guitars under Examination
Having discussed the acoustical / mechanical parameters of the resonator which are the most significant for the features of a guitar and for their effect on the sound, as well as and their evolution over the last two decades, we can now look at each of the instruments under investigation as a whole, finding for each of them the most relevant characteristics.
6.1 Zontini-Replica of the 1862 Torres guitar
Notice first of all from (Tables 1 and 3) the resonance of the air (the ‘tuning note’), occurring at 84.5 Hz (therefore between E2 at 82.407 Hz and F2 at 87.307 Hz on the sixth string). We would expect a higher frequency of the air from an undersized instrument like this; despite the limited volume (10.7 lt.), this resonance was brought to very low values by reducing the natural frequency of the soundboard to 108 Hz, i.e. lower than the Helmholtz resonance (found at 143 Hz). This setup, unusual in more recent guitars, is however compatible with the physical behaviour of the three (soundboard, backboard, body air) coupled oscillators
Such a low natural frequency of the soundboard 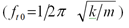 is basically due to its low global stiffness (31650 N/m), while the vibrating mass is rather considerable (69 g). Lacking further information, we may assume the soundboard to be very thin (hence very flexible) and quite heavily braced - typical of old-fashioned guitars. These results are indirectly confirmed in the Romanillo’s text Antonio de Torres - Guitar maker -His Life and Work - Element Books Ltd 1977 where the author reports measurements on guitar soundboards from Torres in the range of 2 mm. or less. Therefore, we should not be surprised that its surface/mass ratio (6.03) is lower than in more recent instruments, due to the soundboard limited vibrating surface (416 cm2) and effective vibrating surface. Moreover, the amplitude of the tuning note at 84.5 Hz is quite small with respect to the resonance of the soundboard at 182.6 Hz. The obvious consequence of this soundboard setting is that even the second basic resonance, or soundboard resonance, occurs at a rather low frequency (183 Hz, so very close to a F3 # on the third string), the result is that the sound texture of this instrument is polarized towards the low register, meaning towards more 'warm' and deep sounds; likely that determined the success of Torres instruments among his contemporaries.
is basically due to its low global stiffness (31650 N/m), while the vibrating mass is rather considerable (69 g). Lacking further information, we may assume the soundboard to be very thin (hence very flexible) and quite heavily braced - typical of old-fashioned guitars. These results are indirectly confirmed in the Romanillo’s text Antonio de Torres - Guitar maker -His Life and Work - Element Books Ltd 1977 where the author reports measurements on guitar soundboards from Torres in the range of 2 mm. or less. Therefore, we should not be surprised that its surface/mass ratio (6.03) is lower than in more recent instruments, due to the soundboard limited vibrating surface (416 cm2) and effective vibrating surface. Moreover, the amplitude of the tuning note at 84.5 Hz is quite small with respect to the resonance of the soundboard at 182.6 Hz. The obvious consequence of this soundboard setting is that even the second basic resonance, or soundboard resonance, occurs at a rather low frequency (183 Hz, so very close to a F3 # on the third string), the result is that the sound texture of this instrument is polarized towards the low register, meaning towards more 'warm' and deep sounds; likely that determined the success of Torres instruments among his contemporaries.
A thin soundboard would not have been able to withstand the strings pull, quite high also at Torres times, even if the vibrating length was less than in modern guitars. Then Torres reinforces the table with braces arranged in a fan shape, and thus obtains a very elastic and limited mass table, able to withstand the pull of the strings. The particular structure of this soundboard tends to support the instrument performance in mid-low registers, while the limited volume of the body tends to favour the manifestation of the air resonances at a comparatively low value. In the decay time diagram (Figure 10) we notice that sustain at the tuning note frequency is quite scarce, in comparison with what we will find in more recent instruments. This is due to losses in the resonator components and to the position of the soundboard natural resonance (108 Hz) with respect to the Helmholtz resonance (143 Hz). Conceivably, the tuning note is strongly present in the recipe of sound but its relatively short duration does not compromise the balance between harmonic components of the sounds. Sustain (in terms of decay time) is good from about 150 Hz to 500 Hz, with a rather slow decay with respect to frequency. This confirms the previous observation about the liveliness of the response in this range of frequency where sustain is presumably good, while it is poor above 500 Hz.
6.2 Gottlob schuster
In this instrument the resonance of the air occurs at a rather high value (140.6 Hz) and the tuning note therefore falls just below D3 on the sixth string (146.83 Hz). Even the second basic resonance occurs at a very high frequency (276 Hz, i.e. near C4 #). In the Gottlob Schuster guitar the theme of the coupling between table and bottom is developed in a totally different way: now the stiffness of the board is extremely high (203000 N / m) - more than six times greater than in Zontini-Torres. The vibrating mass (73 gr) is higher than the Zontini- Torres, both at upper limits compared to current standards. Not knowing the real thickness of the soundboard in this guitar, we assume that it is rather high (thicknesses in the range of 3 mm or more were common in guitars at the beginning of 19th century), such that the soundboard alone could be able to withstand the pull of the strings, hence the bracing is reduced to only some transversal bar. The consequence is a high stiffness of the table and a very high table natural frequency too. However both the coupling coefficient soundboard- air (0.79) and the vibrating surface (360 cm2) are lower than normal today. Considering that the estimate of the real surface of the table is around 910 cm2, the vibrating surface / real surface ratio is 0.39. The item of the vibrating (or effective) surface is particularly interesting. Next (Table 5) reports the ratio between real (geometric) and effective surface in some of the instruments under examination, the ratio between surface and mass and the ratio between the square of the surface and the mass.
Looking to the table is evident that the real soundboard surface in ancient instruments is smaller than in modern ones: this is a characteristic which allows to recognize immediately an old, undersized, instrument. Nevertheless more significant is the effective vibrating area (and its ratio with the real one): in the best instruments its absolute value can be similar or higher than in the more recent ones, in close relationship to the features of the table bracing: the larger is this ratio, the more the vibrating soundboard and the underlying bracing exploit the wood. But increasing the area of the soundboard involves increasing the mass (and losses) and decreasing the sound radiation: the ratio surface to mass is an indicator of how strong the radiation from the vibrating surfaces (monopoles) will be, a feature clearly related to the loudness of the instrument.
|
Guitar |
Real surface [cm2] |
Effective surface [cm2] |
Vibrating mass [gr] |
Effective surf. / real surf. ratio |
Surface / mass ratio |
(Surface)2 / mass ratio |
|
|
Zontini -Torres |
~ 900 |
416 |
69 |
0.46 |
6.03 |
2.51 |
|
|
Gottlob Schuster |
910 |
360 |
73 |
0.39 |
4.93 |
1.77 |
|
|
Fleta |
~ 1300 |
617 |
101 |
0.47 |
6.12 |
3.77 |
|
|
Simplicio |
~ 1420 |
417 |
49 |
0.30 |
8.56 |
3.57 |
|
|
Gallinotti |
1450 |
571 |
74 |
0.39 |
7.75 |
4.43 |
|
|
Garrone |
1450 |
489 |
58 |
0.34 |
8.50 |
4.16 |
|
The compromise surface - mass is highlighted by the ratio - given in the last column of the table - between the square of the surface and the mass. The higher is this ratio, the higher is the coupling between the soundboard and the body air. It comes to evidence, from the table, that this ratio was tending to grow during the development of the guitar, passing from 2-3 in ancient instruments to 4- 5 in more recent ones. At the end, this reflects the effort to increase the instruments effectiveness by designing the soundboards (including the braces) as wide and light as possible.
6.3 Fleta
About sixty years pass between this instrument dated 1921 and the 1862 Torres guitar (replicated by the Luthier Zontini). The design criteria emerging from the analyzes are very different, but the actual results do not show significant improvements in performance. The estimated volume of air in the body (12 liters) is slightly higher than that of the Torres-Zontini (10.7 liters) and the Gottlob Schuster (7 liters) guitars but lower than in more recent instruments (from Simplicio onward), what show, as already noted, the tendency to progressively increase the volume of the body. The Helmholtz resonance occurs at a frequency (143 Hz) substantially equal to that of the Torres guitar, because the greater volume is 'contrasted' by the larger diameter of the hole (87.3 mm). The air resonance F1 appears at 115 Hz - corresponding to the A2 # while the soundboard resonance F2 occurs at 230 Hz. Notice that F2 is exactly twice F1, a situation which is believed to be optimal by many manufacturers.
After examining this instrument, the most significant feature we point out is the considerable stiffness (137229 N / m) and weight (101 gr.) of the soundboard with respect to the average values found in other instruments. Despite a noticeable vibrating surface, the surface / mass ratio (6.12) and the (surface)2 / mass ratio (3.77) are poor. Lacking additional information, we can assume that the ' basic' table is particularly thick, what is found in many ancient instruments where the thickness of the table reaches 3 mm and, at the same, time, the system of bars and braces is altogether heavy. The Gottlob Schuster is another significant example of this tendency. As a consequence, the natural frequency of the soundboard Ft0 is equally high (186 Hz, (Table 1) leading to high values of the basic resonances F1 and F2 if compared with the standards of the most modern guitars, but also with the Torres-Zontini guitar. Despite the considerable amplitude of the basic resonances, the decay time diagram (Figure 10) shows how amplitudes rapidly decrease within the total low - mid frequency band, up to 400 Hz. In other words, sustain is poor and the tuning note - even if present - is short lived in the recipe of sound. This is typical of a ‘tympanic’ sound, probably due to friction losses in the heavy soundboard.
6.4 Modern guitars (Simplicio, Gallinotti, Garrone)
The Simplicio guitar is the first 'modern' guitar among those considered. Certainly not the first in absolute, as this model probably derives from a post-Torres development which proceeds to Simplicio through Manuel Ramirez and Garcia and leads to contemporary manufacturers (including Gallinotti), who most likely went back to the Simplicio model.
|
Guitar |
Air resonance F 1 [Hz] |
Soundboard resonance F 2[Hz] |
Soundboard natural freq. F t0 [Hz] |
|
|
Simplicio |
96 |
193 |
144 |
|
|
Gallinotti |
104 |
221 |
177 |
|
|
Garrone |
95 |
200 |
147 |
|
Firstly in the three guitars here presented the plantilla (the shape) is very similar and the volume almost equal ( 14 liters) but, surprisingly enough, their basic resonances occur at very different values, what indicates a different approach to the problem of exploiting the body air through the coupling between soundboard and Helmholtz resonator (Table 6).
Looking to this table, it seems plausible to gather - in the Gallinotti guitar - the intention to reach in the sound texture a more brilliant sound by raising the tuning note up to G2 #, while in the other two guitars the target was to obtain a slightly darker sound by positioning the tuning note between F2 # and G. These experimental findings (the measured values of the resonance frequencies) are coherent with values of the internal parameters obtained from the model (Table 7).
|
Guitar |
Soundboard natural frequency F t0 [Hz] |
Soundboard stiffness [ N / m] |
Vibrating mass [gr.] |
Vibrating surface [cm2] |
Surface / mass ratio |
Coupling coefficient |
|
Simplicio |
144 |
39884 |
49 |
417 |
8.56 |
0.86 |
|
Gallinotti |
177 |
91400 |
74 |
571 |
7.75 |
0.91 |
|
Garrone |
147 |
49000 |
58 |
489 |
8.50 |
0.895 |
In comparison with the other guitars, the Gallinotti adopts a much stiffer board, resulting in a considerably higher natural soundboard frequency which - in turn - produces much higher basic resonances. A stiff soundboard is favorable to the formation of high frequency vibration modes. In Gallinotti the vibrating surface is higher thanks to a high coupling coefficient. However, due to a high vibrating mass, the surface to mass ratio is rather poor comparing with the Simplicio or the Garrone guitars.
7. Conclusions
The purpose of this study is to analyze the acoustical characteristics of a romantic guitar from Gottlob Schuster, seen in the perspective of a number of guitars built over a period of time ranging from the first decades of the 19th century up to our own days. At this moment the casuistry of the instruments that we could examine is rather scarce, therefore - I believe - sufficient for finding some of the evolutionary lines that identify their character and, at the same time, for fixing some ideas on the design criteria of the ancient instruments and their 'objective' performance with respect to the more recent ones. However I am aware that this analysis is not sufficient to fully understand the criteria according to which the instruments built in the first decades of the nineteenth century were designed. For example, one may ask why some luthiers of the first decades of the 19th century (such as - for example - Guadagnini in Italy or Grobert in France, or our Gottlob Schuster in Austria) chose their specific shape. In those days the outline of the guitar was not yet fixed and the luthiers felt free to define their shape using certain patterns that were the legacy of a tradition and a culture at least 200 years old. We think of recurrent figures such as the Vesica Piscis or the golden rectangle, but also of the evidence of geometric constructions based on 'centers of curvature' (which define the bouts and the waist of the guitar) falling close to points characteristic of the outline (for example the center of the hole or of the bridge). These correlations exist in a way more or less evident in all ancient guitars, with similar (but not equal) characteristics. Similar but not equal, and this has led to the differentiation - over the years - in the shape of the instrument mediated by the personal creativity of the builders.
Given therefore that the geometric correlations I have mentioned cannot be due only to randomness or aesthetic taste, I think they reflect the ideas that the ancient luthiers had on the acoustics of the guitar and on its way of working, ideas they shared with violin makers. For example, a common opinion was that the lobes of the instrument (guitar but also violin) were able to reflect the sound waves within the body, concentrating the sound in their respective centers of curvature; from that assumption resulted the choice of placing these centers in strategic positions, such as the center of the bridge or the center of the hole. Obviously, luthiers of past times could not take advantage of research and manufacturing methods which are available today. The evaluation of the few historical guitars presented in the course of this article was accomplished by means of the measurement and investigation criteria focused on the course of our studies on the classical guitar. Our attempt was always to approach these instruments with caution and utmost respect, even when actual data emerged from analyses raised doubts about the convenience of certain choices.
Acknowledgements
I’m grateful to Dr. Marco Bazzotti, physicist, guitar and mandolin player, researcher. His expertise on the history of the guitar and its composers is definitely recognized. He gave me the opportunity of examining its own Gottlob Schuster guitar.
The measurements were accomplished by Luthier Mario Garrone, co-author of the book ‘Classical Guitar Design’ already mentioned. Since many years Mario Garrone and myself we share ideas, opinions, results of our investigations as well as the tools with which these investigations are accomplished. The study on the Gottlob Schuster guitar is not an exception.
References
- Cuzzucoli G, Garrone Classical Guitar Design. Springer, Cham (2020).
- Romanillos JL. Antonio de Torres, Guitar Maker: His Life and Work. Element Books L. td, Longmead (1977).
- Evans T, Evans MA. Guitars. Music, History, Construction and Players From the Renaissance to Rock. Paddinton Press, New York (1977).


 Impact Factor: * 2.8
Impact Factor: * 2.8 CiteScore: 2.9
CiteScore: 2.9  Acceptance Rate: 11.01%
Acceptance Rate: 11.01%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 