Applied Adsorption Kinetics Model for Removal of Hazards from Aqueous Solution: More Informational Parameters for Industrial Design
Article Information
Song Lou*
Department of Biological Systems Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 24061, United States
*Corresponding Author: Song Lou, Department of Biological Systems Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 24061, United States, Tel: +15402317601;
Received: 18 September 2017; Accepted: 22 September 2017; Published: 27 September 2017
View / Download Pdf Share at FacebookAbstract
Adsorption is one of the widely applied techniques for removal of hazards from aqueous solution. Its kinetics studies are of great significance to evaluate the adsorption performance and reveal the underlying mechanisms. There are several mathematic models to describe the adsorption process and diffusion mode. In recently years, more and more adsorption kinetics models with more informational parameters are investigated, which could give guidance for industrial conversion through supplying paramount importance parameters. Here, we reviewed several widely used adsorption kinetics models and paid more attention to their potential values of industrial application guiding. We believe that the review is of certain significance and improvement of applied adsorption kinetics modeling.
Keywords
Adsorption kinetics models, Industrial conversion, Wastewater treatment, Kinetics parameters
Adsorption kinetics models articles Adsorption kinetics models Research articles Adsorption kinetics models review articles Adsorption kinetics models PubMed articles Adsorption kinetics models PubMed Central articles Adsorption kinetics models 2023 articles Adsorption kinetics models 2024 articles Adsorption kinetics models Scopus articles Adsorption kinetics models impact factor journals Adsorption kinetics models Scopus journals Adsorption kinetics models PubMed journals Adsorption kinetics models medical journals Adsorption kinetics models free journals Adsorption kinetics models best journals Adsorption kinetics models top journals Adsorption kinetics models free medical journals Adsorption kinetics models famous journals Adsorption kinetics models Google Scholar indexed journals Industrial conversion articles Industrial conversion Research articles Industrial conversion review articles Industrial conversion PubMed articles Industrial conversion PubMed Central articles Industrial conversion 2023 articles Industrial conversion 2024 articles Industrial conversion Scopus articles Industrial conversion impact factor journals Industrial conversion Scopus journals Industrial conversion PubMed journals Industrial conversion medical journals Industrial conversion free journals Industrial conversion best journals Industrial conversion top journals Industrial conversion free medical journals Industrial conversion famous journals Industrial conversion Google Scholar indexed journals Wastewater treatment articles Wastewater treatment Research articles Wastewater treatment review articles Wastewater treatment PubMed articles Wastewater treatment PubMed Central articles Wastewater treatment 2023 articles Wastewater treatment 2024 articles Wastewater treatment Scopus articles Wastewater treatment impact factor journals Wastewater treatment Scopus journals Wastewater treatment PubMed journals Wastewater treatment medical journals Wastewater treatment free journals Wastewater treatment best journals Wastewater treatment top journals Wastewater treatment free medical journals Wastewater treatment famous journals Wastewater treatment Google Scholar indexed journals Kinetics parameters articles Kinetics parameters Research articles Kinetics parameters review articles Kinetics parameters PubMed articles Kinetics parameters PubMed Central articles Kinetics parameters 2023 articles Kinetics parameters 2024 articles Kinetics parameters Scopus articles Kinetics parameters impact factor journals Kinetics parameters Scopus journals Kinetics parameters PubMed journals Kinetics parameters medical journals Kinetics parameters free journals Kinetics parameters best journals Kinetics parameters top journals Kinetics parameters free medical journals Kinetics parameters famous journals Kinetics parameters Google Scholar indexed journals nature articles nature Research articles nature review articles nature PubMed articles nature PubMed Central articles nature 2023 articles nature 2024 articles nature Scopus articles nature impact factor journals nature Scopus journals nature PubMed journals nature medical journals nature free journals nature best journals nature top journals nature free medical journals nature famous journals nature Google Scholar indexed journals water quality articles water quality Research articles water quality review articles water quality PubMed articles water quality PubMed Central articles water quality 2023 articles water quality 2024 articles water quality Scopus articles water quality impact factor journals water quality Scopus journals water quality PubMed journals water quality medical journals water quality free journals water quality best journals water quality top journals water quality free medical journals water quality famous journals water quality Google Scholar indexed journals wastewater treatment articles wastewater treatment Research articles wastewater treatment review articles wastewater treatment PubMed articles wastewater treatment PubMed Central articles wastewater treatment 2023 articles wastewater treatment 2024 articles wastewater treatment Scopus articles wastewater treatment impact factor journals wastewater treatment Scopus journals wastewater treatment PubMed journals wastewater treatment medical journals wastewater treatment free journals wastewater treatment best journals wastewater treatment top journals wastewater treatment free medical journals wastewater treatment famous journals wastewater treatment Google Scholar indexed journals environmental pollution articles environmental pollution Research articles environmental pollution review articles environmental pollution PubMed articles environmental pollution PubMed Central articles environmental pollution 2023 articles environmental pollution 2024 articles environmental pollution Scopus articles environmental pollution impact factor journals environmental pollution Scopus journals environmental pollution PubMed journals environmental pollution medical journals environmental pollution free journals environmental pollution best journals environmental pollution top journals environmental pollution free medical journals environmental pollution famous journals environmental pollution Google Scholar indexed journals Soil articles Soil Research articles Soil review articles Soil PubMed articles Soil PubMed Central articles Soil 2023 articles Soil 2024 articles Soil Scopus articles Soil impact factor journals Soil Scopus journals Soil PubMed journals Soil medical journals Soil free journals Soil best journals Soil top journals Soil free medical journals Soil famous journals Soil Google Scholar indexed journals
Article Details
1. Removal of Hazards from Aqueous Solution
Recent advances in environment science and engineering suggest that many of the current problems involving water quality could be greatly diminished using porous adsorption resin [1]. It has recently been demonstrated that porous-structured materials and particle exhibit good adsorption efficiency especially due to their high surface area and greater amount of active sites for interaction with toxic metallic species [2-8]. However, there is less attention on the potential practice-guiding impact of related adsorption model. A variety of adsorption kinetic and induction force models, like pseudo first order, Langmuir and Freundlich models, which are widely used in the treatment study of wastewater, are used to try to investigate the mechanism of adsorption process [9-15]. In recent years, the study of adsorption models, which could indicate the applied parameters, such as adsorption equilibrium time and optimal adsorbent pore size, is being researched extensively [16-18]. These models are expected to be applied prosperously since the supplied parameters are very vital to optimize the design of the industrial adsorption system.
As scientists begin to identify the adsorption mechanisms that contribute to separation efficiency, more informed and personalized removal strategy of hazard from aqueous solution can be developed. This increased insight has led to the directed design of adsorption kinetics models that better exploit the physical and chemical properties of adsorbent. For instance, in industrial scale objects, the adsorbent and adsorbate are in contact with each other for a short time period, therefore, predicating the equilibrium time and the rate of adsorption is of paramount importance [19-22]. Meanwhile, differences in particle size and the pore nature of the adsorbent plays a very important role in the efficiency of the adsorption process [23-26]. The better description of adsorbent size contribution could supply a better guidance for the adsorbent size selection in big-scale application of water treatment.
Many hypotheses have been considered to describe the adsorption kinetic and various theoretical and empirical models have been presented for modeling of adsorption kinetics. The classical adsorption kinetics model, Langmuir kinetics model (equation 1): assumes the surface of adsorbate is energetically homogeneous [27-28].
?
(pA is adsorbate’s partial pressure; V is the volume of adsorbate; ?A is the fractional occupancy of the adsorption sites; Vm is the volume of the monolayer; Keq is the associated equilibrium constant). By contrast, the Langmuir-Freundlich model (equation 2) is another equation, which can’t be solved analytically and considers the effect of surface heterogeneity [29-31]. However, the rate constant of this model can be obtained by an approximation method.
?
(ΦA is the fractional occupancy of the adsorption sites; ?F and CF are fitting parameters)
The other two important empirical rate models: pseudo first order (equation 3) and pseudo second order (equation 4): could supply a better validity under certain conditions [32-34].
?
(k1 is the pseudo first order rate coefficient; qe and q are the amount of the adsorbed species per unit mass of adsorbent at the equilibrium state and any time of adsorption)
?
(k2 is the pseudo second order rate coefficient)
All these classical adsorption kinetics models are used generally in the study of wastewater treatment to investigate the adsorption mechanism [21, 35-39]. However beside the traditional adsorption theory, they cannot give any specific guidance parameter for the industry-scale application. As more and more lab research of wastewater began to be transformed via industrial conversion, more informative process parameters needs to be developed from kinetics model to guide industrial production. In 2017, Azizian et al. reported that the shape of the adsorption kinetic curve could be described by the mathematical model of hyperbolic tangent properly (equation 5) [16] Followed by the traditional model deduction process, the y and x were defined as ?and x=kt. When the equilibrium state is set as q/qe?0.995, the adsorption kinetics model could be described as? ?. In addition to consider the different degrees of curvature of kinetics curves, which are derived from the adsorbent surface heterogeneity, different functional groups on the ad-species, possibility of binding to the surface with different geometries, and effect of diffusion on the adsorption overall rate, the n power law was introduced for the curvature degree:
?
(te is the required time for adsorption to reach the equilibrium state; ? is the setting of q/qe?0.995; n is power constant)
This hyperbolic tangent model was evaluated through three different data series on two different testing conditions: adsorption same concentration of adsorbate onto the different amount of adsorbent; different concentration of adsorbate onto the same concentration of adsorbent. For the different amount of adsorbent, the values of the equilibrium time derived from hyperbolic tangent model decreased by increasing the adsorbent dosage. For the different amount of adsorbate, the equilibrium time, te, increased by increasing the adsorbate concentration in solution.
The predicted equilibrium times of adsorption by the hyperbolic tangent kinetic model are very similar to the experimental ones. This model is simple and can be used easily for modeling of adsorption kinetics data in industrial scales to give the equilibrium time of adsorption. This predicted equilibrium time is much useful for controlling the industrial wastewater treatment process, which could benefit the industrial design and production cost. It is a perfect example of how basic science of model and engineering go hand in hand. This work investigated the model with the restriction setting of equilibrium state as q/qe >0.995. Actually, this model cannot only be used under this scale, but also any designed equilibrium degree. So it could accurately predict the equilibrium time in any setting scale of q/qe according to the experiment needed. By leveraging our ever-growing knowledge of wastewater adsorption and its kinetics model, it is possible to engineer a progressive hyperbolic tangent kinetics models to give more industrial-guiding parameters under more flexible equilibrium definition.
Recently, rates of adsorption have been observed to exhibit biphasic behavior: a rapid adsorption in the order of minutes followed by a slower phase with a timescale in the order of hours [40-41]. The latter phase, which may result in a significant fraction being sequestered, [42-44] is frequently rate limiting for abstraction and separation [45-47]. Mechanism proposed as potentially responsible for the commonly observed slow adsorption of hazards on resins includes intraorganic matter diffusion [48, 49] and hindered pore diffusion [50-52]. Diffusion through hazardous materials is analogous to diffusion in polymers; i.e, diffusing molecules must penetrate and migrate through a polymeric matrix [53]. Pore diffusion can be either sterically hindered or retarded by sorption to organic phases associated with pore wells. Adsorption on high-energy sites may also be an important rate-limiting step. In condensed polymeric organic matter, active compounds may adsorb strongly in molecule-sized voids or “holes” [54] while during pore diffusion they are subject to high-energy sorption in molecule-sized pores [55-56]. Now, adsorption has been modeled both as a diffusive and as a first-order rate process. Several different rate models have been used to describe the adsorption of active compounds onto adsorbent.
Different groups have carried out adsorption kinetics studies. Norris et al. presented the first experimental evidence to produce a three-parameter model (equation 6) to describe adsorption rates for both a slowly adsorbing fraction and a rapidly desorbing fraction [57-58]. The model’s parameters are useful for distinguishing the rapidly and slowly adsorbing compartments. An advantage of this model is that its parameters are useful for distinguishing between rapidly and slowly adsorbing fractions.
?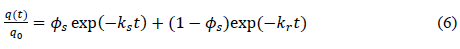
(?s is fast adsorption rate coefficient; ks is fast adsorption rate; kr is slow adsorption rate; t is adsorption time, q(t) is adsorption amount (mg/g) at the time of t; q0 is initial adsorption amount(mg/g).
Furthermore, model results are intuitive given the biphasic nature of the adsorption data. Noort et al.stated a technique using Tenax TA beads as a “sink” for the solute was employed to measure the kinetics of adsorption and desorption of chlorobenzenes, polychlorinated biphenyles from laboratory-contaminated sediment [59]. They suggested a three-compartment model (equation 7) in which the slow fraction is divided into two compartments, slowly and very slowly adsorbing. An advantage of this model is that it theoretically describes a continuous distribution of sorptive compartments with only two parameters. However, convergence on a five-parameter solution was laborious and uncertain, with final fitted parameters strongly depending on initial guesses; researchers rarely recommend the triphasic model over others.
?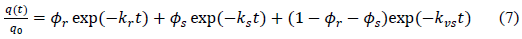
(?s is fast adsorption rate coefficient; ks is fast adsorption rate; kr is slow adsorption rate; t is adsorption time, q(t) is adsorption amount (mg/g) at the time of t; q0 is initial adsorption amount (mg/g))
Shuler studied a new two-parameter model (equation 8) to express the kinetics of adsorption based on the gamma function, which assumes the adsorption and desorption from heterogeneous sites occurs over a continuum of energies and rates [60]. This model theoretically describes a continuous distribution of adsorptive compartments with only two parameters. An advantage of this model is that it theoretically describes a continuous distribution of sorptive compartments with only two parameters. However, the gamma model underpredicted adsorption at late stages as it “flattened out” too much, indicating that the model does not mechanistically describe the observed adsorption process; the two calculated parameters do not have obvious physical significance and do not logically correlate to observed trends in slow adsorption rates and resistant fractions.
?
(Daq is the diffusion coefficient; ?g is the density of the adsorbate; ?i is the intrapariticle porosity; ?f is the tortuosity factor)
Roberts and Gschwend used a one-parameter spherical pore-diffusion model (equation 9) to describe the experimental data of adsorption, which only has one fitting parameter, and it can theoretically estimate adsorption rates a priori based on adsorbate and adsorbent physical characteristics [61]. Advantages of this model are that it has only one fitting parameter, and it can theoretically estimate adsorption rates a priori based on sorbate and sorbent physical characteristics. However, the simple spherical pore-diffusion model often does not fit entire adsorption rate profiles, and it essentially has no rapidly adsorbing fraction.
?
(Cr is the immobile aqueous-phase concentration, r is the radial coordinate; Da is the apparent diffusion coefficient)
Although there are several reports about the adsorption kinetics of resins, all of them attribute the adsorption to a simple process without considering the effect of sphere size. Corroll and Berens suggested a three-parameter, two-compartment model (equation 10) accounting for the influence of sphere diameter, which assumed biphasic polymer diffusion processes [62]. They studied rates of adsorption of solutes to poly-(vinyl chloride) polymer powders of non-uniform particle size and found that a simple modification of the Fickian model satisfactorily accounts for the effect of particle non-uniformity upon sorption kinetics for conditions under which transport is diffusion-controlled. This monophasic model always gives a good fit of data in each case, however the adsorption is not considered as rapid, slow and even slower procedures, but only a global process instead.
?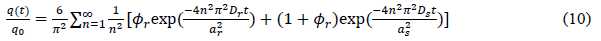
(?r is fast adsorption rate coefficient; ar and as are the diameters of the spheres; Dr and Ds are diffusion coefficient)
My study was performed in order to determine the adsorption profiles of adsorbate on resins functionalized with chloromethy and amino groups [63-64]. A new adsorption isotherm model, the multi-layer inductive effect model (equation 11): in which the inductive effect passed to a higher layer, and a new adsorption kinetics model (equation 12): the multi-compartment kinetics model, in which the adsorption process contained more compartments, were created according to the multiparameter theory and Karickhoff’s theory by investigating the regression of the experimental results [65].
?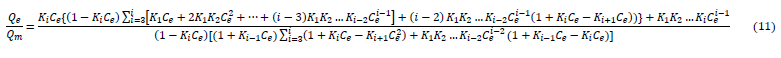
?(K1, K2,?, Ki are the equilibrium adsorption constants for the first layer, second layer,?,i th layer, respectively; ?1, ?1,?, ?i are the fracitions of surface overage at the first layer, second layer,?, i th layer, respectively; Ce is the equilibrium adsorbate concentration; Qm is the surface site density )
?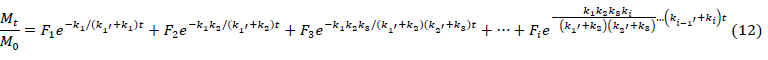
? (F1, F2,?, Fi are different compartments fractions; k1, k2,?, ki are the rate constants of every adsorption level; k1’, k’2,?, ki’ are the rate constants of every desorption level, respectively; M0 is mass present at t=0)
These new models explained the adsorption process better than the other kinetic models, and provided a good fit of adsorption data, which is not surprising in that they had at least two more fitting parameters than any of the other models. In order to guide the industry application, a sphere size parameter was considered to be included to explain adsorption kinetics more explicitly. Previous studies have demonstrated that due to the repulsive or attractive action between adsorbate and adsorbent, adsorption of multiple components can be rationally expected to be either competitive or synergistic. In some studies, [41, 45, 56, 66] weeks or months of incubation for the adsorption systems were tested in order to make sure the sorption equilibrium was achieved. In fact, some previous studies have shown that aging a long time has negligible additional effect on adsorption-resistant fractions or adsorption rates. The equilibration time is based on several factors, such as driving force, sphere diameter, and the concentration of the solution. The effects of driving force, solution concentration and sphere size on the adsorption process have been discussed in our previous work [67].
Comparison of experimental data with Fick’s Law requires a solution of the diffusion equation appropriate for the sample geometry and experimental boundary conditions. The simplest geometry for powder is a collection of spherical particles of uniform size. This condition can, in fact, be closely approached in specific powder prepared by emulsion polymerization. Consequently, to approximate adsorption of adsorbate by synthetic resins, we made a model for the adsorption on nonuniform resins in the case of uniform initial concentration throughout the sphere, a constant concentration at the surface, and constant Dr. According to the theory of the first-order, two-component four-parameter model, a new model [68] incorporating sphere size can be described by the following equitation 13:
?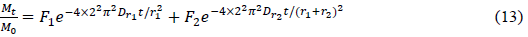
(Mt?is the solid-phase sorbate concentration at a given time, M0?is the initial solid-phase adsorbate concentration, F1?and F2?are different compartments’ fractions, Dr?is the diffusion coefficient, and r1?and r2?are the diameters of the spheres, on which the different compartments of adsorption process are mainly carried out)
It should be noted, however, that this first-order, two-compartment, four-parameter model does not necessarily reflect the reasonable procedures of adsorption. This model contains just two steps, and does not take into account the differences be- tween fast adsorption, slow adsorption, and even slower adsorption [69]. Accordingly, a modified model with sphere size was created according to Karickhoof’s theory and the multiparameter adsorption kinetics model. A sphere-size model in which the adsorption process contains more compartments was proposed as equation 14.
?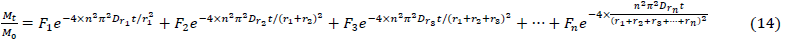
The terminated layer of the adsorption was determined by the multilayer polarity inductive effect model (equation 11).
Through studying the adsorption processes of same adsorbate on different resins and comparing the fitting results of different models, the values of R2 from the sphere-size kinetics were identical with our previous multiparameter kinetics model. Meanwhile, this model supplied very useful parameters, which reflects the effect of sphere-size distribution on adsorption kinetics process. This sphere-size model was created to present the first experimental evidence that sphere size affects the adsorption process. The new sphere-size model has more detailed parameters to more accurately describe the adsorption process, and will assist in the development of an efficient, industrial wastewater purification process. However, this model still lacks several important parameters, which could guide the industrial-scale production better, such as equilibrium time.
Overall, the progress toward adsorption kinetics models with more detailed parameter is encouraging, and this is hope that further development of new adsorption theory will help to bring forth better industrial outcomes.
References
- Tratnyek PG, Johnson RL. Nanotechnologies for environmental cleanup. Nano today 1 (2006): 44-48.
- Diallo MS, Savage N. Nanoparticles and water quality. Journal of Nanoparticle Research 7 (2005): 325-330.
- Mazzaro R, Boni A, Valenti G, et al. Uniform Functionalization of High-Quality Graphene with Platinum Nanoparticles for Electrocatalytic Water Reduction. Chemistryopen 4 (2015): 268-273.
- Hwang S, Martinez D, Perez P, et al. Effect of surfactant-coated iron oxide nanoparticles on the effluent water quality from a simulated sequencing batch reactor treating domestic wastewater. Environ. Pollut 159 (2011): 3411-3415.
- Jones LA, Ogden KL. Silica and titania nanoparticles impact on water quality: Experiments involving Ralstonia pickettii in nutrient-rich and poor media. Environ Prog Sustain 32 (2013): 279-284.
- Zaluzhna O, Li, Y, Allison, TC, et al. Inverse-Micelle-Encapsulated Water-Enabled Bond Breaking of Dialkyl Diselenide/Disulfide: A Critical Step for Synthesizing High-Quality Gold Nanoparticles. JACS 134 (2012): 17991-17996.
- Son J, Vavra J, Forbes VE. Effects of water quality parameters on agglomeration and dissolution of copper oxide nanoparticles (CuO-NPs) using a central composite circumscribed design. Sci. Total Environ 521 (2015): 183-190.
- Bielefeldt AR, Stewart MW, Mansfield E, et al. Effects of chlorine and other water quality parameters on the release of silver nanoparticles from a ceramic surface. Water Res 47 (2013): 4032-4039.
- Jewell KS, Castronovo S, Wick A, et al. New insights into the transformation of trimethoprim during biological wastewater treatment. Water Res 88 (2016): 550-557.
- de Souza SMDGU, Bonilla KAS, de Souza AAU, et al. Removal of COD and color from hydrolyzed textile azo dye by combined ozonation and biological treatment. J. Hazard. Mater 179 (2010): 35-42.
- Kluczka J, Korolewicz T, Zolotajkin M, et al. Boron removal from water and wastewater using new polystyrene-based resin grafted with glycidol. Water Resour Ind 11 (2015): 46-57.
- Lakshmanan R, Sanchez-Dominguez M, Matutes-Aquino JA, et al. Removal of Total Organic Carbon from Sewage Wastewater Using Poly(ethylenimine)-Functionalized Magnetic Nanoparticles. Langmuir 30 (2014): 1036-1044.
- Efremenko, I, Sheintuch, M, Predicting solute adsorption on activated carbon: Phenol. Langmuir 22 (2006): 3614-3621.
- Singh KP, Mohan D, Sinha S, et al. Color removal from wastewater using low-cost activated carbon derived from agricultural waste material. Industrial & Engineering Chemistry Research 42 (2003): 1965-1976.
- Amin MT, Alazba AA, Shafiq M. Adsorptive Removal of Reactive Black 5 from Wastewater Using Bentonite Clay: Isotherms, Kinetics and Thermodynamics. Sustainability-Basel 7 (2015): 15302-15318.
- Eris S, Azizian S. Analysis of adsorption kinetics at solid/solution interface using a hyperbolic tangent model. J. Mol. Liq 231 (2017): 523-527.
- Plazinski W, Rudzinski W, Kinetics of Adsorption at Solid/Solution Interfaces Controlled by Intraparticle Diffusion: A Theoretical Analysis. J Phys Chem C 113 (2009): 12495-12501.
- Rudzinski W, Plazinski W. On the applicability of the pseudo-second order equation to represent the kinetics of adsorption at solid/solution interfaces: a theoretical analysis based on the statistical rate theory. Adsorption 15 (2009): 181-192.
- Isiuku BO, Anyanwu DC, Nwosu CN, et al. Batch adsorptive removal of metanil yellow from simulated dye wastewater using nitric acid modified-H3PO4-activated carbon (NAMPAAC) from Gmelina arborea bark: equilibrium and isotherm studies. Desalin Water Treat 70 (2017): 380-386.
- Mahmoodi NM, Salehi R, Arami M. Binary system dye removal from colored textile wastewater using activated carbon: Kinetic and isotherm studies. Desalination 272 (2011): 187-195.
- Malik PK, Dye removal from wastewater using activated carbon developed from sawdust: adsorption equilibrium and kinetics. J. Hazard. Mater 113 (2004): 81-88.
- Wang CT, Chou WL, Chung MH, et al. COD removal from real dyeing wastewater by electro-Fenton technology using an activated carbon fiber cathode. Desalination 253 (2010): 129-134.
- Reddy DD, Ghosh RK, Bindu JP, et al. Removal of Methylene Blue from Aqueous System Using Tobacco Stems Biomass: Kinetics, Mechanism and Single-Stage Adsorber Design. Environ Prog Sustain 2017, 36 (4): 1005-1012.
- Guo YF, Deng J, Zhu JY, et al. Removal of mercury(II) and methylene blue from a wastewater environment with magnetic graphene oxide: adsorption kinetics, isotherms and mechanism. Rsc Adv 6 (2016): 82523-82536.
- Sen, T. K, Afroze, S, Ang, H. M, Equilibrium, Kinetics and Mechanism of Removal of Methylene Blue from Aqueous Solution by Adsorption onto Pine Cone Biomass of Pinus radiata. Water Air Soil Poll 2011, 218 (1-4): 499-515.
- Kannan N, Sundaram MM. Kinetics and mechanism of removal of methylene blue by adsorption on various carbons - a comparative study. Dyes Pigments? 51 (2001): 25-40.
- Nasernejad B, Zadeh TE, Pour BB, et al. Camparison for biosorption modeling of heavy metals (Cr(III): Cu(II): Zn(II)) adsorption from wastewater by carrot residues. Process Biochem 40 (2005): 1319-1322.
- Rengaraj S, Moon SH. Kinetics of adsorption of Co(II) removal from water and wastewater by ion exchange resins. Water Res 36 (2002): 1783-1793.
- Raghunath S, Anand K, Gengan RM, et al. Sorption isotherms, kinetic and optimization process of amino acid proline based polymer nanocomposite for the removal of selected textile dyes from industrial wastewater. J Photoch Photobio B 165 (2016): 189-201.
- Khorramfar S, Mahmoodi NM, Arami M, et al. Equilibrium and kinetic studies of the cationic dye removal capability of a novel biosorbent Tamarindus indica from textile wastewater. Color Technol 126 (2010): 261-268.
- Al-Ghouti MA, Khraisheh MA, Allen SJ, et al. The removal of dyes from textile wastewater: a study of the physical characteristics and adsorption mechanisms of diatomaceous earth. J. Environ. Manage 69 (2003): 229-238.
- Ho YS, McKay G. Pseudo-second order model for sorption processes. Process Biochem 34 (1999): 451-465.
- Ho YS, McKay G. A comparison of chemisorption kinetic models applied to pollutant removal on various sorbents. Process Saf. Environ. Prot 76 (1998): 332-340.
- Ho YS. Review of second-order models for adsorption systems. J. Hazard. Mater 136 (2006): 681-689.
- Demirbas E, Kobya M, Senturk E, et al. Adsorption kinetics for the removal of chromium (VI) from aqueous solutions on the activated carbons prepared from agricultural wastes. Water Sa 30 (2004): 533-539.
- Sun QY, Yang LZ. The adsorption of basic dyes from aqueous solution on modified peat-resin particle. Water Res 37 (2003): 1535-1544.
- Hameed BH, Din ATM, Ahmad AL. Adsorption of methylene blue onto bamboo-based activated carbon: Kinetics and equilibrium studies. J. Hazard. Mater 141 (2007): 819-825.
- Qiu H, Lv L, Pan BC, et al. Critical review in adsorption kinetic models. J Zhejiang Univ-Sc A 10 (2009): 716-724.
- Putra EK, Pranowo R, Sunarso J. Indraswati, N, Ismadji, S, Performance of activated carbon and bentonite for adsorption of amoxicillin from wastewater: Mechanisms, isotherms and kinetics. Water Res 43 (2009): 2419-2430.
- Carroll KM, Harkness MR, Bracco AA, et al. Application of a Permeant Polymer Diffusional Model to the Desorption of Polychlorinated-Biphenyls from Hudson River Sediments. Environ. Sci. Technol 28 (1994): 253-258.
- Pignatello JJ, Ferrandino FJ, Huang LQ. Elution of Aged and Freshly Added Herbicides from a Soil. Environ. Sci. Technol 27 (1993): 1563-1571.
- Steinberg SM, Pignatello JJ, Sawhney BL. Persistence of 1,2-Dibromoethane in Soils - Entrapment in Intraparticle Micropores. Environ. Sci. Technol 21 (1987): 1201-1208.
- Juang RS, Shiau JY. Adsorption isotherms of phenols from water onto macroreticular resins. J. Hazard. Mater 70 (1999): 171-183.
- Kanazaki T, Hirawa S, Harada M, et al. Coupled Acoustic-Gravity Field for Dynamic Evaluation of Ion Exchange with a Single Resin Bead. Anal. Chem 82 (2010): 4472-4478.
- Kukkonen JVK, Landrum PF, Mitra S, et al. Sediment characteristics affecting desorption kinetics of select PAH and PCB congeners for seven laboratory spiked sediments. Environ. Sci. Technol 37 (2003): 4656-4663.
- Naef R, Acree WE. Calculation of Five Thermodynamic Molecular Descriptors by Means of a General Computer Algorithm Based on the Group-Additivity Method: Standard Enthalpies of Vaporization, Sublimation and Solvation, and Entropy of Fusion of Ordinary Organic Molecules and Total Phase-Change Entropy of Liquid Crystals. Molecules 22 (2017).
- Chen MS, Fan HF, Lin KC. Kinetic and thermodynamic investigation of rhodamine B adsorption at solid/solvent interfaces by use of evanescent-wave cavity ring-down spectroscopy. Anal. Chem 82 (2010): 868-877.
- Wegner GJ, Wark AW, Lee HJ, et al. Real-time surface plasmon resonance imaging measurements for the multiplexed determination of protein adsorption/desorption kinetics and surface enzymatic reactions on peptide microarrays. Anal. Chem 76 (2004): 5677-5684.
- Nkedikizza P, Brusseau ML, Rao PSC, et al. Nonequilibrium Sorption during Displacement of Hydrophobic Organic-Chemicals and Ca-45 through Soil Columns with Aqueous and Mixed-Solvents. Environ. Sci. Technol 23 (1989): 814-820.
- Llewellyn PL, Maurin G, Devic T, et al. Prediction of the conditions for breathing of metal organic framework materials using a combination of X-ray powder diffraction, microcalorimetry, and molecular simulation. JACS 130 (2008): 12808-12814.
- Bourrelly S, Llewellyn PL, Serre C, et al. Different adsorption behaviors of methane and carbon dioxide in the isotypic nanoporous metal terephthalates MIL-53 and MIL-47. JACS 127 (2005): 13519-13521.
- Sapsford KE, Tyner KM, Dair BJ. Deschamps, J. R, Medintz, I. L, Analyzing Nanomaterial Bioconjugates: A Review of Current and Emerging Purification and Characterization Techniques. Anal. Chem 83 (2011): 4453-4488.
- Pignatello JJ, Xing BS. Mechanisms of slow sorption of organic chemicals to natural particles. Environ. Sci. Technol 30 (1996): 1-11.
- Xing BS, Pignatello JJ. Dual-mode sorption of low-polarity compounds in glassy poly(vinyl chloride) and soil organic matter. Environ. Sci. Technol 31 (1997): 792-799.
- Salles F, Ghoufi A, Maurin G, et al. Molecular Dynamics Simulations of Breathing MOFs: Structural Transformations of MIL-53(Cr) upon Thermal Activation and CO2 Adsorption. Angew Chem Int Edit 47 (2008): 8487-8491.
- Farrell J, Grassian D, Jones M. Investigation of mechanisms contributing to slow desorption of hydrophobic organic compounds from mineral solids. Environ. Sci. Technol 33 (1999): 1237-1243.
- Berens AR, Hopfenberg HB. Diffusion and Relaxation in Glassy Polymer Powders .2. Separation of Diffusion and Relaxation Parameters. Polymer 19 (1978): 489-496.
- Berens AR. Diffusion and Relaxation in Glassy Polymer Powders .1. Fickian Diffusion of Vinyl-Chloride in Polyvinyl Chloride). Polymer 18 (1977): 697-704.
- Connaughton DF, Stedinger JR, Lion LW, et al. Description of Time-Varying Desorption-Kinetics - Release of Naphthalene from Contaminated Soils. Environ. Sci. Technol 27 (1993): 2397-2403.
- Grathwohl P, Reinhard M. Desorption of Trichloroethylene in Aquifer Material - Rate Limitation at the Grain Scale. Environ. Sci. Technol 27 (1993): 2360-2366.
- Harmon TC, Roberts PV. Comparison of Intraparticle Sorption and Desorption Rates for a Halogenated Alkene in a Sandy Aquifer Material. Environ. Sci. Technol 28 (1994): 1650-1660.
- Berens AR, Huvard GS. Particle-Size Distribution of Polymer Powders by Analysis of Sorption Kinetics. J. Dispersion Sci. Technol 2 (1981): 359-378.
- Lou S, Chen ZB, Liu YF, et al. Synthesis of Functional Adsorption Resin and Its Adsorption Properties in Purification of Flavonoids from Hippophae rhamnoides L. Leaves. Industrial & Engineering Chemistry Research 51 (2012): 2682-2696.
- Lou S, Di D. Synthesis of resins with ionic liquids for purification of flavonoids from Hippophae rhamnoides L. leaves. J. Agric. Food. Chem 60 (2012): 6546-6558.
- Lou S, Chen Z, Liu Y, et al. New way to analyze the adsorption behavior of flavonoids on macroporous adsorption resins functionalized with chloromethyl and amino groups. Langmuir 27 (2011): 9314-9326.
- Dallabetta RA. Carbon-Monoxide Adsorption on Supported Ruthenium. J. Phys. Chem 79 (1975): 2519-2525.
- Lasakova M, Jandera P. Molecularly imprinted polymers and their application in solid phase extraction. J. Sep. Sci 32 (2009): 799-812.
- Lou S, Liu YF, Bai QQ, et al. Adsorption Mechanism of Macroporous Adsorption Resins. Prog Chem 24 (2012): 1427-1436.
- Wegner GJ, Wark AW, Lee HJ, et al. Real-time surface plasmon resonance imaging measurements for the multiplexed determination of protein adsorption/desorption kinetics and surface enzymatic reactions on peptide microarrays. Anal. Chem 76 (2004): 5677-5684.


 Impact Factor: * 3.6
Impact Factor: * 3.6 CiteScore: 2.9
CiteScore: 2.9  Acceptance Rate: 11.01%
Acceptance Rate: 11.01%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 