1. Introduction

The four-color problem forms the famous four-color conjecture. The four-color conjecture is available for any flat-picture graph   such that,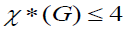 . The four-color lemma has seen extensive research in graph theory, but the problem is NP-hard and computer results proved convincing in edge-dyed [2], surface-dyed [3, 4] , and color-dyed [1, 8]  with a restricted strip. In the literature above, the methods of proof commonly used in mathematics, such as the traditional direct proof method, the reverse proof method, the mathematical induction method, etc., and the graph theory proves its unique method and technology, such as the shortest (long) path method, and the maximum edge method [1, 5, 8].

2. The Development of Dyeing Theory

The process of applying the weight transfer method is based on the handshake lemma. Let G be a connected plane graph, then according to Euler theorem;

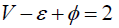
Where is the number of vertices of G, the number of edges of G is ε, and the number of planes of G is ϕ. The handshake lemma [2, 5, 9]  sets G as a communication flat graph, and that, 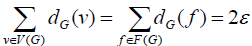Where F(G)is the face set of G.

If we set G as a connected flat chart, for any real number k,l>0; following constant equation is established: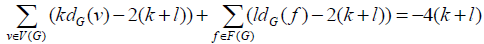

3. Power Transfer Method

Applying Euler Formula 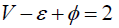and handshaking lemma,

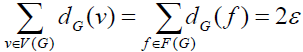explains the sum of the initial rights as a constant. By using the nonexistence of reducible sub-graphs, it is shown that the total number of new weight sums is different from the total number of initial weight sums [2, 10], and thus obtains the contradiction. It is proven that such a minimal counterexample of G does not exist [12, 13], so the graph belonging to C has the P attribute.

For any, 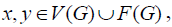We remember 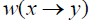denotes the weight transferred from x to y. To begin with, every element in 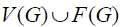, the graph G remains unchanged; 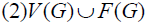the new weight of each element is not negative, which contradicts the Euler formula. In practice, this is often the case: Yes, arbitrary

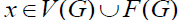defines graph G as follows:

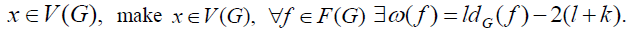
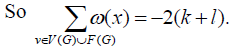
This follows that,

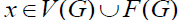. The weights of each element are adjusted to 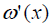. Since it is only transferred within the elements, the addition and retention of the graph remains the same, that is, 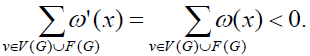Furthermore we define an appropriate weight transfer rule, and verify that each conforms to a certain rule structure, such as the result obtained 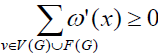which is a contradiction, and the conclusion is proved.

Below 4 cases:

We give an example to illustrate the application of weight transfer method [7, 9]. Let G be a simple plan, and 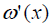if 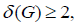, Then one of the following conditions holds:

(I) G contains a 2-point adjacent to a 2-point;

(II) G contains a 3-point adjacent to a 2-point and a ≤ 3-point;

(III) G contains a d-point adjacent to (d -1) 2-points, where d ≥ 4

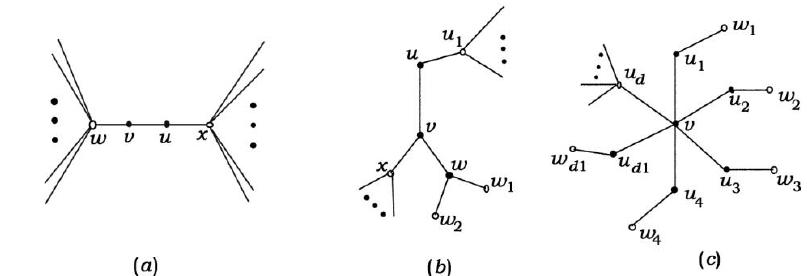
It is proved that G is the least reverse example to meet the example condition, and the Euler defined formula 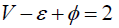can be rewritten into the following form;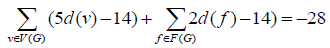

 Then, 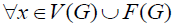defines the initial weight function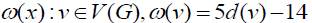

provided that 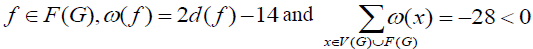The transfer of power method is then used to obtain a new number of ω', where the rules for transfer of power are as follows:

(R1): Transfer from each ≥3 point to each of its adjacent 2-points is 2

(R2); Transfer from each ≥4 point to each of its adjacent vertex v, if d(v)=2, then there is a transfer 2 to d(v)=3, from1

we proved that,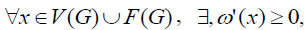 , and that is a contradiction.

The set F(G) is such that, 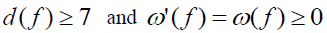. Set v is any vertex of Figure G, if d(v)=2 the

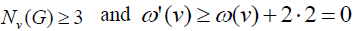such that, d(v)=3 is attached to the N_v(G). Thus all the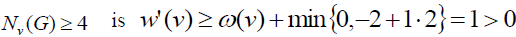

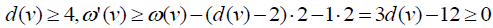and that

and that

Thus, 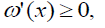as proved.

References

1. West DB. Introduction to graph theory. Upper Saddle River, NJ: Prentice hall 2 (1996). 
2. Gross JL, Yellen J (Eds.). Handbook of graph theory. CRC press (2004).
3. Bondy JA, Murty USR. Graph theory with applications. London: Macmillan 290 (1976). 
4. Godsil C, Royle GF. Algebraic graph theory. Springer Science and Business Media 207 (2013). 
5. Bollobás B. Modern graph theory. Springer Science and Business Media 184 (2013). 
6. Biggs N, Biggs NL, Norman B. Algebraic graph theory. Cambridge university press 67 (1993). 
7. Golumbic MC. Algorithmic graph theory and perfect graphs. Elsevier 57 (2004). 
8. Forson R. Hamiltonicity of Total Domination 3-Connected Edge Critical Graph. Available at SSRN 2941978 (2017).
9. Gross JL, Tucker TW. Topological graph theory. Courier Corporation (2001). 
10. Forson R, Guanghui C, Ofori S, et al. The Distribution Properties of Two-Parameter Exponential Distribution Order Statistics.
11. Gibbons A. Algorithmic graph theory. Cambridge university press (1985).
12. Golumbic MC. Algorithmic graph theory and perfect graphs. Elsevier 57 (2004).
13. Forson R, Nweit OT. A Generalization of Probabilistic Cauchy-Schwarz Inequality. Available at  SSRN3080064 (2017).