Predicting Supercritical Extraction of St. John’s Wort by Simple Quadratic Polynomial Model and Adaptive Neuro-Fuzzy Inference System- Firefly Algorithm
Ramin Tahmasebi Boldaji*1, Hossein Rajabi Kuyakhi2
1Department of Chemical Engineering, College of Engineering, University of Isfahan, P.O. Box 81746-73441, Isfahan, Iran
2Department of Chemical Engineering, University of Guilan, Rasht 41996-13769 Iran
*Corresponding Author: Ramin Tahmasebi Boldaji. Department of Chemical Engineering, College of Engineering, University of Isfahan, P.O. Box 81746-73441, Isfahan, Iran
Received: 17 May 2021; Accepted: 25 May 2021; Published: 28 May 2021
Article Information
Citation: Ramin Tahmasebi Boldaji, Hossein Rajabi Kuyakhi. Predicting Supercritical Extraction of St. John’s Wort by Simple Quadratic Polynomial Model and adaptive neuro-fuzzy inference system- firefly algorithm: A comparison study. Journal of Analytical Techniques and Research 3 (2021): 14-27.
View / Download Pdf Share at FacebookAbstract
In this study, the applicability of the adaptive neuro-fuzzy inference system (ANFIS) and response surface methodology (RSM) was evaluated to forecasting the supercritical extraction of St. John’s Wort. In this case, the ANFIS model was optimized by the firefly algorithm (FFA) to develop the performance of the model. The accuracy of the models was investigated by comparing the result of the models with experimental data. The precision of the RSM model has been investigated using statistical analysis (P-value<0.05, F-value=148.13, R2=0,99 R2 Adjusted=0.98, R2 Predicted =0.96). The data transfer power was proved by the Box-Cox plot. Also, the polynomial model shows that it is much simpler and easier than other complex models. The results show, the ANFIS-FFA with R2=0.99, RMSE=1.79 and AARD%=2.79 have a high capability of predicting the St. John’s Wort extraction amount
Keywords
<p>St. John’s Wort, RSM, ANFIS, Supercritical fluid, Statistical analysis</p>
Article Details
1. Introduction
Hypericum perforatum L. (St. John’s wort) is a plant that grows in Asia, Europe, and the north of Africa [1,2]. Attention on this plant has risen because of the anti-depressant and anti-cancer properties of its extraction [3-5]. Recently, Supercritical solvents morally use [6]. Different parameters such as temperature and solvent/plant ratio are effective on extraction efficiency [7]. Catchpole et al Extracted St. John’s wort using supercritical carbon dioxide at pressures of 250 and 300 bar and 313 K and at 300 K; and 323 K with ethanol as co-solvent [8]. Manila et al studied the effect of fluid density, time, and temperature of supercritical extraction for the separation of hyperforin and adhyperforin [9]. The results showed that the extraction is strongly dependent on the supercritical carbon dioxide density. Glisic et al investigated the extraction of hyperforin and adhyperforin from St. John's Wort (Hypericum perforatum L.) by supercritical carbon dioxide Supercritical extraction in a semi-batch autoclave [10]. Extractions were investigated at three different pressures at temperatures of 313 and 323 K. The results showed that increasing the pressure increases the extraction.
In contrast to conventional methods, the interaction between variables can be determined by statistical techniques [11-15]. In recent years, machine learning approaches is attracted researchers’ interest in the modeling of different processes [16-22]. Kunjiappan et al [23] used Response surface methodology and adaptive neuro-fuzzy inference system to the analysis of ultrasound-assisted extraction of bioactive polyphenols from Garcinia indicia. Esfe and Kamyab [24] applied the ANN and RSM-based method to study the relative thermal conductivity (RTC) and relative viscosity (RV) of alumina nanoparticles (Al2O3 NPs) in water as nanofluid (NF). Geyikçi, et al [25] established response surface methodology (RSM) and artificial neural network (ANN) to predict the lead removal from industrial sludge.
In this work, the ANFIS, ANFIS-FFA and RSM were applied for the prediction of supercritical carbon dioxide extraction. The result obtained were compared with the experimental data. The models showed good agreement with the actual data. Statistical analysis confirmed the adequacy of the ANFIS -FFA model.
2. Methods
2.1 Experimental data
In this investigation, St. John’s wort extractions yield were collected in a previous article [10,5] to develop an ANFIS model in analogy with the RSM model. The dried St. John’s Wort was obtained from southern Serbia. The particle size was about 400 µm and the moisture content was 7.55wt %. Supercritical extraction was performed in a semi-batch Autoclave Engineers Screening System at 313 and 323 K and 10, 15 and 20 Mpa. To evaluate the ANFIS model performance the collected data divided into 70% and 30% for train and test, respectively.
3. MODELS
3.1 ANFIS
ANFIS was proposed by Jang and Sun [26]. This learning technique is more flexible because of combining the learning law with Fuzzy rules [27,28]. Because of this advance, it became a powerful technique for function approximation application. There are five layers in the ANFIS structure, which is shown in Figure 1. ANFIS includes a fuzzification layer, normalized layer, defuzzification layer, and an output layer. adaptive nodes create a fuzzy set of input quantities in the first layer. In the second layer, the weight of the rules (wi) resulted by multiplying the input values of nodes by each other. The normalization of the weight of rules happens in the third layer. Defuzzification is fulfilled in the fourth layer, and finally, the output is extracted [22]. In this study, the ANFIS model was proposed through the Takagi and Sugeno type of fuzzy rules.to this aim, a Gaussian membership function has been used. As, mentioned to develop the model dataset was divided into 30% for a test and 70% for a train. The detail of the developed ANFIS structure reported in Table 1. To this aim, temperature (K), pressure (MPa), and m CO2/m plant (g/g) were used to predict extraction values. The ANFIS model shows the high capability to estimate the extraction values with R2=0.979 and R2= 0.98 for test and train respectively.
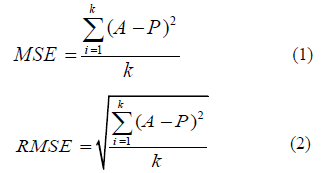
|
Parameters |
Description |
|
Fuzzy type |
Sugeno |
|
Mf function |
Gaussian |
|
Initial FIS |
Genfis 3 |
|
No. MF |
4 |
|
No . Input |
3 |
|
No. Output |
1 |
|
Optimal method |
Hybrid |
|
Max epoch |
2000 |
|
Initial step size |
0.001 |
|
Step size decrease rate |
0.059 |
|
Step size increase rate |
0.95 |
Table 2: Detail of ANFIS model structure.
3.2 ANFIS-FFA model
The FFA as an intelligent algorithm was first reported by Yang [29]. This algorithm is being extremely applied to resolve diverse complex optimization problems. More details about the FFA and its adjustment can be found in the literature [30]. In the modeling of the ANFIS-FFA, the
selection of appropriate quantities of the γ, β0, α,
the number of iteration and population size have the most effect on the performance of ANFIS-FFA [31]. T train the ANFIS-FFA, trial and error method was selected and based on the results, the values of 1, 2, 0.98, 1500, and 45 were selected for the γ, β0, α, a number of iteration and population size, respectively.
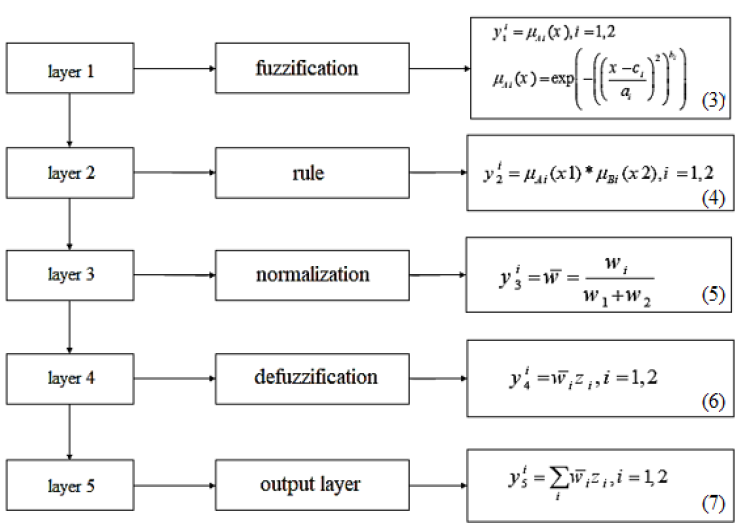
Figure 1: Layer structure of ANFIS model.
3.3 Experimental design
Design-Expert Software provides powerful tools to layout an ideal experiment on process, mixture or combination of factors and components. This software presents comparative experiments, screening, characterization, optimization and combined designs [32] and provides test matrices for screening up to 50 factors. Statistical significance of these factors is established with an analysis of variance (ANOVA). ANOVA is provided to establish statistical significance. Graphical tools help identify the impact of each factor on the eligible results [33]. In this study, central composite design (CCD) with three levels and three parameters) temperature K, pressure MPa and m CO2/m plant g/g) was used to predict the extraction amount. In this modeling, a simple quadratic equation is obtained for this purpose. Analysis of variance (ANOVA) was used to evaluate the regression coefficients (Table1).
|
Model |
Sum of squares |
Df |
Mean square |
F-value |
P-value |
|
2547.5 |
6 |
424.58 |
148.13 |
<0.0001 significant |
|
|
A- m (CO2)/m (plant) |
2178.18 |
1 |
2178.18 |
759.93 |
<0.0001 |
|
B- pressure |
67.3 |
1 |
67.3 |
23.48 |
0.0013 |
|
C- temperature |
128.27 |
1 |
128.27 |
44.75 |
0.0002 |
|
AC |
38.73 |
1 |
38.73 |
13.51 |
0.0063 |
|
A2 |
318.65 |
1 |
318.65 |
111.17 |
<0.0001 |
|
B2 |
36.39 |
1 |
36.39 |
12.7 |
0.0074 |
|
Residual |
22.99 |
8 |
2.87 |
|
|
|
R2Adjusted=0.98 |
|
|
|
|
|
|
R2Predicted=0.95 |
|
|
|
|
|
|
C.V.%=5.38 |
|
|
|
|
|
Table 1: Analysis of variance quadratic polynomial model.
3.3.1 Quadratic Response Surface: In this study, a quadratic model is needed to obtain the proper performance. A quadratic polynomial model can express the results. The regression model performed is as follows [34]:
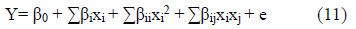
In the second-order polynomial model, Y is the response value, and Xi and Xj is independent variables. Regression coefficients, βi is a linear coefficient, βij is a quadratic coefficient, βii is an interaction coefficient, and β0 is a constant. Also, i, j and e are the error terms. Equation 7 is a polynomial model of actual coefficients which shows the amount of extraction by supercritical fluid.
M (extract)/m (plant) = +0.85867 + [10.27119 × (m (CO2)/m (plant)] + [5.06266 × pressure] - [0.120363 × temperature] - [0.034742 × [(m (CO2)/m (plant)]2 ] - [0.024742 × (m (CO2)/m (plant) × temperature ] - [0.151149 × pressure2] (12).
The overall prediction ability and statistical significance of the model are evaluated by the R2 coefficient and Fisher test(F-value) [35]. But the value of R2 alone cannot indicate the adequacy of the model. For this reason, the adjusted R2 coefficient is also used. Box-Cox Chart (Figure 2) shows the data transfer power [6]. The lowest point on this chart represents the best transition. The value of P is less than 0.05. The values of R2 are also close to 1. These values indicate the adequacy of the model obtained [6,34,36].
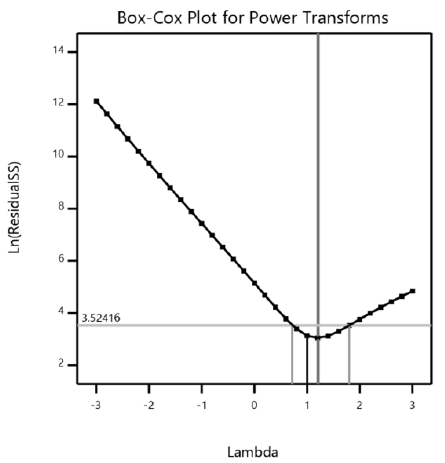
Figure 2: Box-Cox plot for power transforms.
4. Model evaluating
The performance of the established models was evaluated by R2, MSE, AARD%, and RMSE in Table 4. From Table 4, the ANFIS-FFA model shows high capability with the lowest error values against ANFIS, and RSM. Also From Figure 3, the regression plot shows the high performance of ANFIS-FFA. Figure 4 illustrates error histograms for trained models. As can be seen, the ANFIS-FFA model has lower error distribution and it prove the accuracy of the ANFIS-FFA model. The deviations quantities obtained by models are shown in Figure 5. It is obviously seen that the lowest deviation is noted for ANFIS-FFA. The average relative deviation percentage values for RSM, ANFIS and ANFIS-FFA are 5,9, 3.9 and 0.025.
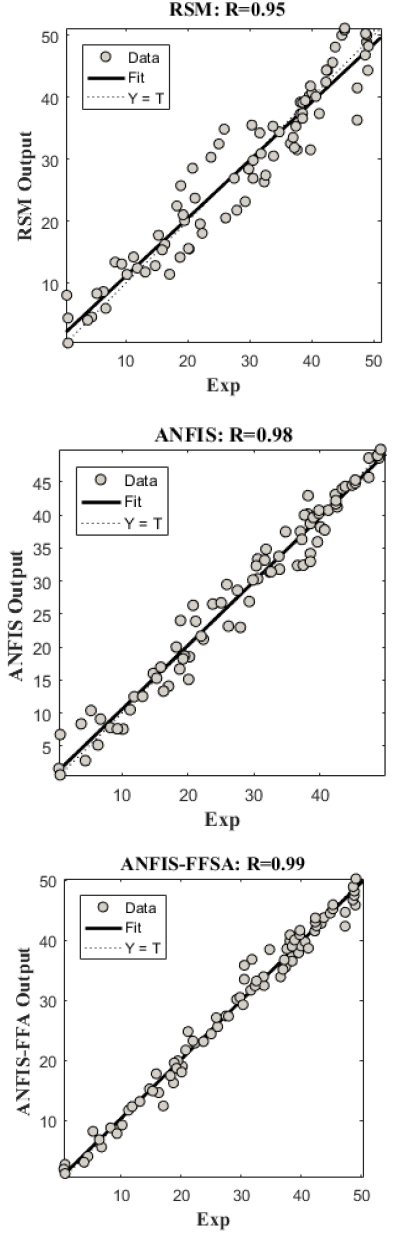
Figure 3: regression plot for ANFIS ANFIS-FFA and RSM
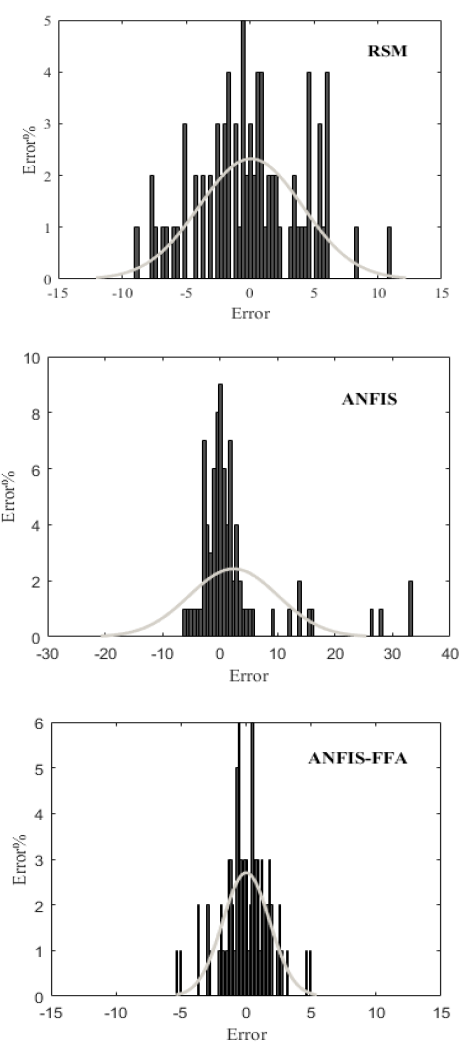
Figure 4: error histogram for ANFIS and RSM
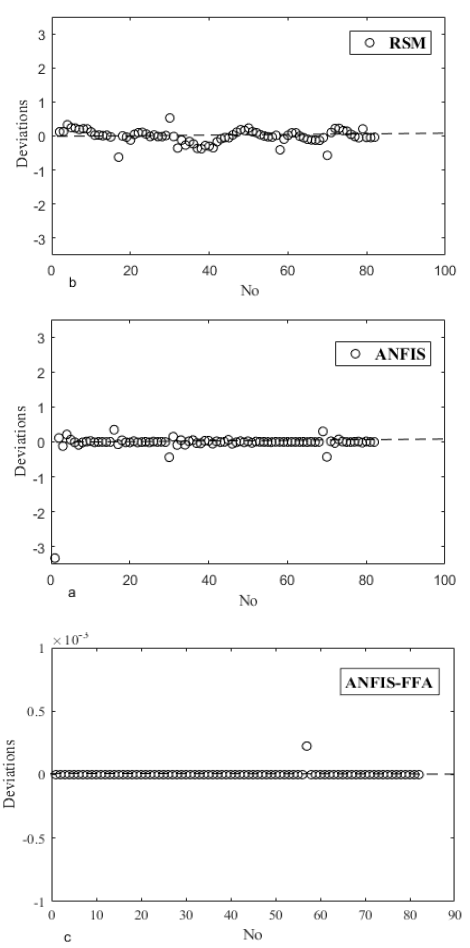
Figure5: deviation plot for a) ANFIS, b) ANFIS-FFA, and c) RSM.
A comparison of the equation obtained by response surface methodology and ANFIS-FFA Output with the experimental data is demonstrated in Figure 6. The graph obtained by the quadratic model and the output of ANFIS-FFA is in good agreement with actual values. Also, the ANFIS-FFA model has the best performance to estimate the extraction amounts based on a statistical parameter is shown in Table 4.
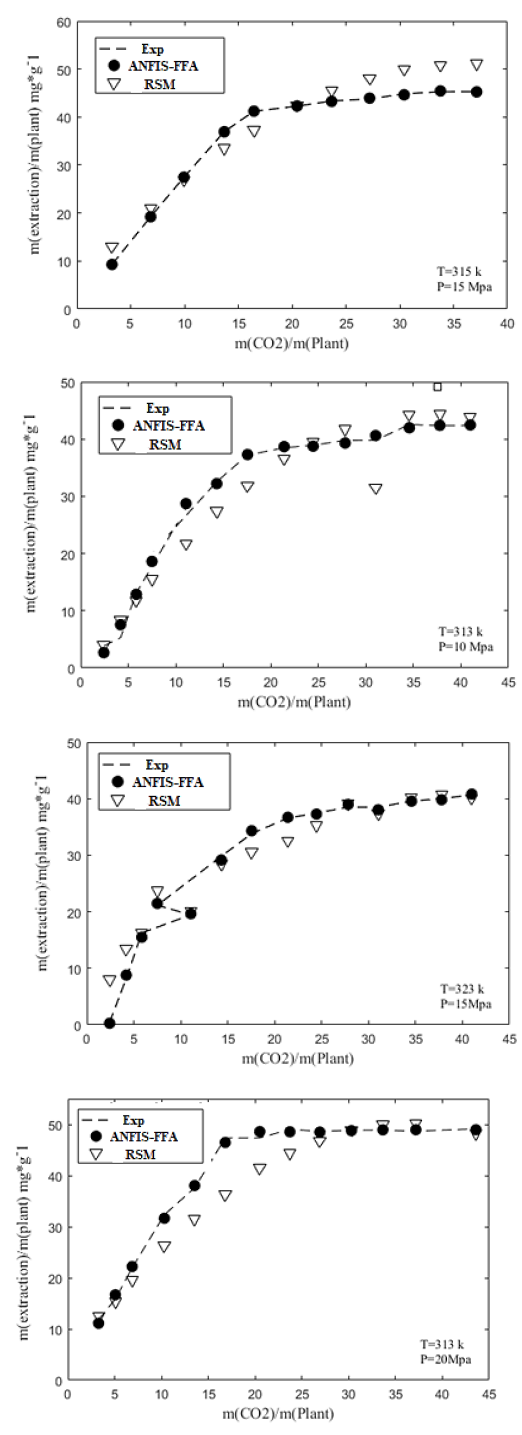
Figure 6: Comparison of quadratic polynomial models with laboratory data
|
Statistical parameters |
ANFIS-FFA |
ANFIS |
RSM |
|
R2 |
0.991 |
0.98 |
0.95 |
|
MSE |
3.21 |
6.01 |
16.12 |
|
RMSE |
1.79 |
2.45 |
4.01 |
|
AARD% |
2.72 |
3.76 |
6.44 |
Table 4: Comparison of ANFIS and RSM based on statistical parameters.
Various factors and parameters affect the extraction of plants. Extraction from the plant by supercritical carbon dioxide changes with a change in pressure and solvent-to-solid ratio. As can be seen from the experimental data, the extraction rate increases with increasing pressure [5]. The extraction rate also increases with increasing fluid to plant ratio. Extraction temperature also increases the extraction efficiency, but excessive temperature destroys the bioactive compounds.
3.5. Sensitivity analysis
Sensitivity analysis was carried to appraise the effect of the input variable on the ANFIS model's performance. The relevancy factor of each parameter was calculated from equation 15.
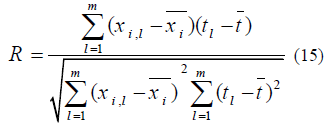
Where xil denotes quantities of lth input, xi is the mean values of the input, tl refers to lth output, and t is attributed to mean values of output [37]. Based on Figure 7, the m CO2/m has the most effect on the performance of the ANFIS-FFA model with the highest importance factor for modeling.
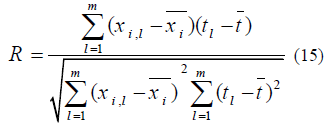
Figure7: Sensitivity analysis using relevancy factor.
5.Conclusion
In this study, RSM and ANFIS methods were used to forecasting the amount of supercritical carbon dioxide extraction from the St. John’s Wort. the ANFIS was optimized with FFA algorithm. The ANFIS-FFA and RSM results were compared with experimental data. The resolute obtained shows the high capability of two models for the prediction of extraction amounts. Statistical analyzes were performed including F values, P-value, R2, r2adj, r2pre, and Box-Cox diagram. R2 values close to 1, low P-values, and F-value indicate the accuracy of the model. Data transfer power was evaluated by the Box-Cox plot. Based on the statistical parameter and graphical method ANFIS-FFA indicated a high capability to predict the amount of supercritical carbon dioxide extraction from the St. John’s Wort. (R2=0.99, MSE=3.21, AARD%=2.72 and RMSE=1.79).
Acknowledgements
The authors are thankful to Masoud Alikhani and Reza Deylam Salehi for their consistent support and whose comments helped in improving the quality and presentation of this article.
Conflicts of Interest:
The authors declare no conflict of interest.
References
- Kirakosyan A, Gibson DM, Kaufman PB. The production of dianthrones and phloroglucinol derivatives in St. John’s Wort. In Bioactive Molecules and Medicinal Plants (2008): 149-164.
- Dolezal R, Houdková I, Kalász H, et al. Determination of Hypericin in Hypericum perforatum (St. John’s Wort) Using Classical C18 and Pentafluorophenyl Stationary Phases: Contribution of Pi-Pi Interactions to High-Performance Liquid Chromatography (HPLC). Analytical Letters 52 (2019): 1788-1812.
- Cao X, Wang Q, Li Y, et al. Isolation and purification of series bioactive components from Hypericum perforatum L. By counter-current chromatography. Journal of chromatography B 879 (2011): 480-488.
- Valletta E, Rinaldi A, Marini M, et al. Distinct Hypericum perforatum L. Total extracts exert different antitumour activity on erythroleukemic K562 cells. Phytotherapy research 32 (2018): 1803-1811.
- Hatami T, Glisic SB, Orlovic AM. Modelling and optimization of supercritical CO2 extraction of St. John's Wort (Hypericum perforatum L.) Using genetic algorithm. The Journal of Supercritical Fluids 62 (2012): 102-108.
- Tahmasebi-Boldaji R, Hatamipour MS, Khanahmadi M, et al. Ultrasound-assisted packed-bed extraction of hypericin from Hypericum perforatum L. And optimization by response surface methodology. Ultrasonics sonochemistry 57 (2019): 89-97.
- Xu DP, Zheng J, Zhou Y et al. Ultrasound-assisted extraction of natural antioxidants from the flower of Limonium sinuatum: Optimization and comparison with conventional methods. Food chemistry 217 (2017): 552-559.
- Catchpole OJ, Perry NB, Da Silva BMT et al. Supercritical extraction of herbs I: Saw Palmetto, St John's wort, Kava root, and Echinacea. The Journal of supercritical fluids 22 (2002): 129-138.
- Mannila M, Kim H, Isaacson C, et al. Optimization of supercritical fluid extraction for the separation of hyperforin and adhyperforin in St. John’s wort (Hypericum perforatum L.). Green Chemistry 4 (2002): 331-336.
- Glisic S, Smelcerovic A, Zuehlke S, et al. Extraction of hyperforin and adhyperforin from St. John's Wort (Hypericum perforatum L.) By supercritical carbon dioxide. The Journal of Supercritical Fluids 45 (2008): 332-337.
- Asadi N, & Zilouei H. Optimization of organosolv pretreatment of rice straw for enhanced biohydrogen production using Enterobacter aerogenes. Bioresource technology 227 (2017): 335-344.
- Kleijnen JP. Experimental design for sensitivity analysis, optimization, and validation of simulation models. Handbook of simulation 173 (1998): 223.
- Khuri AI, & Mukhopadhyay S. Response surface methodology. Wiley Interdisciplinary Reviews: Computational Statistics 2 (2010): 128-149.
- Kleijnen JP. Experimental design for sensitivity analysis, optimization, and validation of simulation models. Handbook of simulation 173 (1998): 223.
- Myers RH, Montgomery DC, Anderson-Cook C M. Response surface methodology: process and product optimization using designed experiments. John Wiley & Sons (2016).
- Lariche MJ, Soltani S, Davoudi Nezhad H, et al. Developing supervised models for estimating methylene blue removal by silver nanoparticles. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, (2019): 1-8.
- Rajabi-Kuyakhi H. Biodiesel Production with Supercritical Ethanol Estimation using RBF-ANN Approach.
- Darvishan A, Bakhshi H, Madadkhani M, et al. Application of MLP-ANN as a novel predictive method for prediction of the higher heating value of biomass in terms of ultimate analysis. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects 40 (2018): 2960-2966.
- Mir M, Kamyab M, Lariche MJ, et al. Applying ANFIS-PSO algorithm as a novel accurate approach for prediction of gas density. Petroleum Science and Technology 36 (2018): 820-826.
- Sayyad Amin J, Rajabi Kuyakhi H, Kashiwao T, et al. Development of ANFIS models for polycyclic aromatic hydrocarbons (pahs) formation in sea sediment. Petroleum Science and Technology 37 (2019): 679-686.
- Baghban A, Ahmadi MA, Pouladi B, et al. Phase equilibrium modeling of semi-clathrate hydrates of seven commonly gases in the presence of TBAB ionic liquid promoter based on a low parameter connectionist technique. The Journal of supercritical fluids 101 (2015): 184-192.
- Kuyakhi HR, Zarenia O, Boldaji RT. Hybrid intelligence methods for modeling the diffusivity of light hydrocarbons in bitumen. Heliyon 6 (2020): e04936.
- Kunjiappan S, Panneerselvam T, Govindaraj S, et al. Optimization and analysis of ultrasound-assisted extraction of bioactive polyphenols from Garcinia indica using RSM and ANFIS modeling and its anticancer activity. Journal of the Iranian Chemical Society 17 (2020): 789-801.
- Esfe MH, Kamyab MH. Mathematical monitoring of agglomeration effects on thermophysical properties of water-based nanofluids using MLP and RSM. Journal of Thermal Analysis and Calorimetry (2020): 1-18.
- Geyikçi F, Kiliç E, Çoruh S, et al. Modelling of lead adsorption from industrial sludge leachate on red mud by using RSM and ANN. Chemical Engineering Journal 183 (2012): 53-59.
- Jang, J. S.. ANFIS: adaptive-network-based fuzzy inference system. IEEE transactions on systems, man, and cybernetics, 23(3) (1993), 665-685.
- Abdulshahed AM, Longstaff AP,Fletcher, S. The application of ANFIS prediction models for hermal error compensation on CNC machine tools. Applied Soft Computing 2 (2015): 158-168.
- Rajabi Kuyakhi H, & Tahmasbi Boldaji R. A novel ANFIS model to prediction of the density of n-alkane in different operational condition. Petroleum Science and Technology 37 (2019): 2429-2434.
- Yang XS. Firefly algorithm. Nat Inspired Metaheuristic Algorithms 20 (2008): 79-90.
- Majumder A, Das A, Das PK. A standard deviation-based firefly algorithm for multi-objective optimization of WEDM process during machining of Indian RAFM steel. Neural Computing and Applications 29 (2018): 665-677.
- Zhou J, Li C, Arslan CA, et al. Performance evaluation of hybrid FFA-ANFIS and GA-ANFIS models to predict particle size distribution of a muck-pile after blasting. Engineering with Computers (2019): 1-10.
- Tanco M, Viles E, Ilzarbe L, et al. Dissecting doe Software. Lean & Six Sigma Review 7 (2008): 25.
- Comley J. Design of Experiments: Useful Statistical Tool in Assay Development or Vendor Disconnect. (2010).
- Zhou Y, Zheng J, Gan RY, et al. Optimization of ultrasound-assisted extraction of antioxidants from the mung bean coat. Molecules 22 (2017): 638.
- Chen F, Zhang Q, Fei S, et al. Optimization of ultrasonic circulating extraction of samara oil from Acer saccharum using combination of Plackett-Burman design and Box-Behnken design. Ultrasonics sonochemistry 35 (2017): 161-175.
- Tahmasebi Boldaji R, Rajabi Kuyakhi H, Tahmasebi Boldaji N. Prediction of 1-butanol and diesel fuel blend heat capacity by response surface methodology. Petroleum Science and Technology (2020): 1-7.
- Golsefatan A, Shahbazi K. Predicting the effect of nanocomposites on asphaltene removal using a comprehensive approach. Petroleum Science and Technology 38 (2020): 64-73.


 Impact Factor: * 2.8
Impact Factor: * 2.8 Acceptance Rate: 77.30%
Acceptance Rate: 77.30%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 