1. Introduction

In this paper, some important properties of order statistics of two-parameter exponential distribution are discussed when the distribution and density functions of a two-parameter distribution is given. We also proved that the random variables X₁, X₂,..., X_n, obeying the two-parameter exponential distribution are not independent of each other, and do not obey the same distribution. Order statistics is a kind of statistics distribution commonly used in statistical theory and application of which there are many research [1-6]. The two parameter exponential distribution is also a very useful component in reliability engineering. This study considers the nature of order statistics. Its density function and distribution functions are respectively [7];

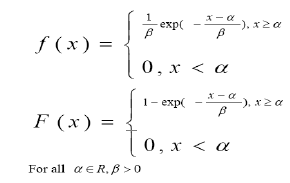
2. Prerequisite Knowledge

2.1 Lemma 1

Let all X follow a continuous distribution function F (x) and its density function of F (x), {a < x < b}, X₁, X₂,...X_n is a simple random sample with acapacity of N from X₂

1. The joint probability density function of (X₁, X ₂,..., X _n) if a ≤ X₁ < X ₂ < ... < X_n ≤ b is

Otherwise,

g_1,2,...,n ( X₁, X ₂, ..., X _n )                    0

2. The joint probability density function of order statistic (Xi, Xj )(1 ≤ I ≤ j ≤ n) is a ≤ x ≤ y ≤ b and

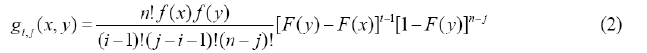
Otherwise,

g_{i, j} (x, y) 0

3. The probability density function of order statistics X (k) is

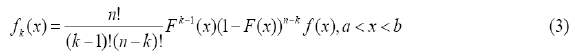
In particular, when k = 1, there is

When k = n, there is

2.2 Lemma 2

Assume that X and Y are two random variables, the joint probability is f (x) if the inequality x₁ ≤ x₂, y₁≤ y₂ is satisfied [10].

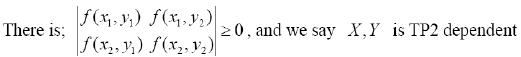
2.3 Lemma 3

For a fixed x, y, if P (X > x, Y > y | X > x¹, Y > y¹ ) is a monotonic increasing function for variables x¹ and y¹, then variables X, Y satisfies RSCI [10] .

2.4 Lemma 4

For any y₁, if P (Y ≤ y₁| X ≤ x₁ ) is monotone decreasing function of x₁, then Y is the left tail decreasing function of X, denoted by Ltd ( XY ) [11].

2.5 Lemma 5

For any y₁, if P (Y > y₁ | X > x₁ ) is an incremental function of x₁, then Y is the right tail growth of X, denoted by RTI (XY) [11].

3. Main Conclusion

3.1 Theorem 1

Let the total X follow a continuous distribution function of F (x) and its density function F (x) (a < x < b), X₁, X₂,..., X_n be a simple random sample with a capacity of N from the population X, and X₁, X₂,..., X_n

1. The order statistics of the joint probability density function of (X₁, X₂,..., X_n ) is as follows; a ≤ X₁ <X₂ < ... <X_n ≤ b

If then

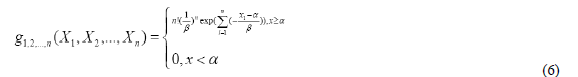
2. The probability density function of X _k is;

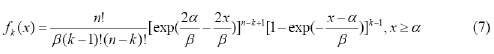
In particular, when k 1, there is

When k= n,

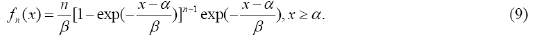
Which is proved from lemma 1.

3.2 Theorem 2

If X₁, X₂, ..., X_n is independent of each other and obeys a two-parameter exponential distribution, then X₁, X₂, ..., X_n is not independent of each other and does not obey the same distribution.

Proof : Let n = 2 be used to represent the observations of x₁ and x₂ with X₁ and X₂ respectively. It can be seen from lemma 1 that the density function of (X₁, X₂) is

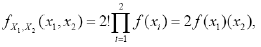
The density functions of X₁ and X ₂ are respectively

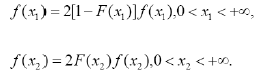
Assuming that X₁ and X ₂ are independent, then f_{X1,X 2} (x₁, x₂ ) = f (x₁ ). f (x₂ ), and 2 f (x₁ ) f (x₂ ) = 2[1- F (x₁)] f (x₁).2F (x₂ ) f (x₂ ) = 4 [1-F (x₁ )]F (x₂ ) f (x₁ ) f (x₂ ).

Therefore,

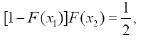
Then,

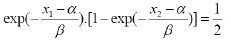
Which obviously does not hold. So

f _{X1, X 2} (x₁, x₂ ) ≠ f (x₁ ). f (x₂)

Therefore, X₁ and X ₂ are not independent of each other and do not obey the same distribution. Hence proved.

3.3 Theorem 3

If X₁, X₂,..., X_n are independent of each other and obey the two-parameter exponential distribution, then X i,Yj (I < j) is TP2 dependent.

Proof: The observations of xi and   xj are represented by Xi, Xj. For any x_i < x_j, the joint density function of Lemma 1, is

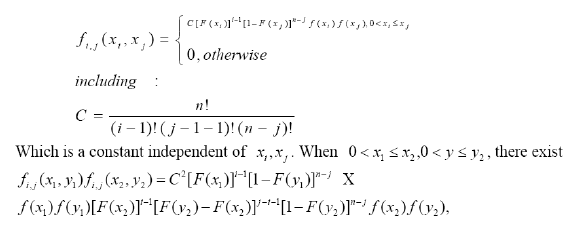
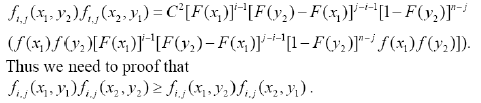
We only need

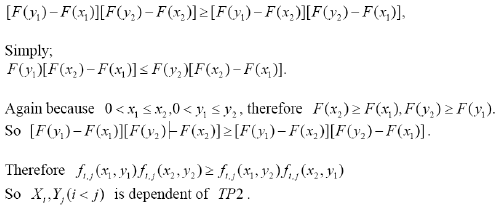
3.4 Theorem 4

Suppose X₁, X₂, ..., X_n is n independent and identically distributed random variables from the exponential distribution of two parameters, then RTI (X_j | X_i), i< j. It is proved that for any             s, t when s > t, there is

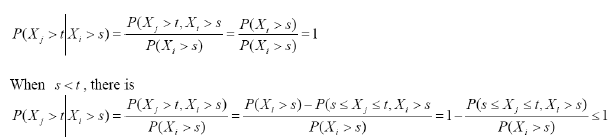
When it is fixed and so increases. The integral of P (≤ X_j ≤ t, Xs) decreases P(s ≤ X_j ≤ t, X_i > s)           

P (X_j > t | Xi > s) LTD( Xi | X_j), i < j according to the density functions becomes smaller and becomes larger.

3.5 Theorem 5

Suppose X_i and X_j are two random variables independently obeying the same two-parameter exponent. Then X₁ and X₂ satisfy RCSI (i.e for fixed X and Y and Y, if P (X x,Y y | X x ', Y y' ) is a monotonic increasing function of variables x' and y', it is proved that the joint density functions of X₁ and X₂ is f_1,2 (x₁, x₂). When x_1, x₂ is invariant,     P( X₁ > x₁, X₂ > x₂ | X₁ > x'₁, X₂ > x'₂ ), x'₁, x'₂ is increasing function

iii When x₁ < x'₁, x₂ > x'₂ or        x₁ > x'x, x₂ < x'₂ are equally available,

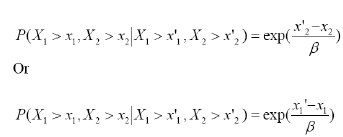
When x_1, x₂ are fixed, they are incremental functions of x'₁, x'₂. In conclusion, P( X₁ > x₁, X₂ > x₂ | X₁ > x'₁, X₂ > x'₂) are incremental functions of x₁ ', x'₂. So X_1, X₂ satisfies RSCI.

4. Conclusion

Some distribution properties of order statistics obeying two-parameter exponential distribution are discussed. It is proved that when X₁, X₂,..., X_n are independent of each other and obey the exponential distribution of two-parameters, the order statistics X₁, X₂, ..., X_n is not independent of each other and does not obey the same distribution, but X_i, X_j satisfies TP2 dependence. For any i < j, there are RTI ( X_j | X_i ), LTD( X_i | X_j), and X_1, X₂ that satisfy RSCI.

References

1. He Jia, Du Chaoxiong. On the Sequencial Satistical Distribution Properties of Exponential Distribution. Journal of Hunan University of science and technology: Natural science edition 26 (2011): 125-128.
2. Jiang Penihua. Distribution properties of Weibull distribution order statistics. Anqing Normal University: NaturalScience Edition 18 (2012): 47-50.
3. Kuang Nenghui. The Distribution Properties Two-parameter Rayleigh Distribution Sequencial Statistics. Journal of Jianxi Normal University: Natural Science Edition 33 (2009): 648-651.
4. Kuangneng Hui. Distribution Properties of Laplace Distribution Sequence. Journal of Xuzhou Normal University: Natural Science Edition 27 (2009): 34-37.
5. Kuangneng Hui. The Distribution properties of Gamma Distribution order statistics. Journal of Lanzhou University of Technology 13 (2010): 17-19.
6. Xiong Jiabing, Wang Zhixing. Properties of Uniform Distribution orderStatistics. Advanced mathematics research 13 (2010): 17-19.
7. Liu Xuan. Accurate formula for calculating the minimum and maximum moments of ordinal statistics of exponential distribution with two parameters. Journal of Zhengzhou University: Science Edition 47 (2015): 41-44.
8. Wang Wei. A Proof of the Distribution Sequential Statistics. Journal of Changchun University 12 (2002): 20-21.
9. He Chaobing, Tian Yanwei. Distribution of Sequential Statistics. Journal of Chengdu University.. Natural Science Edition 27 (2008) : 116-119.
10. Jin Liqin. Statistical Characteristics of Index Distribution and Geometric distribution. Shanghai: Shanghai Normal University (2013).
11. Ave’rous J, Dortet-Bernadet JL. LTD and RTD dependence ordering. Canadian Journal of Statistics 28 (2000): 15-157.