Classification of 7 Arrhythmias from ECG Using Fractal Dimensions
Article Information
Kourosh Kiani*, Farzane Maghsoudi
Department of Electrical and Computer Engineering, Semnan University, Semnan, Iran
*Corresponding Authors: Kourosh Kiani, Department of Electrical and Computer Engineering, Semnan University, Semnan, Iran
Received: 05 June 2019; Accepted: 21 June 2019; Published: 05 July 2019
Citation: Kourosh Kiani, Farzane Maghsoudi. Classification of 7 Arrhythmias from ECG Using Fractal Dimensions. Journal of Bioinformatics and Systems Biology 2 (2019): 053-065.
View / Download Pdf Share at FacebookAbstract
The statistics indicate a dramatic increase in mortality due to cardiovascular failures in the worldwide. In developing countries, with lower per capita income, especially in rural areas, late diagnosis of the disease leads to the sudden death of people. Since electrocardiogram (ECG) is one of the most important tools for diagnosing cardiovascular diseases, this study has been presented to analyze this highly inexpensive and available signal. Extracted characteristics of the signal are a good representation of the heart function because of the chaotic, dynamic, and non-linear behavior of the heart. The fractal dimension is the best representative of the ECG signal which is able to take into account its hidden complexity. ECG signals are analyzed based on the fractal dimension and Back Propagation Neural Network (BPN). In this paper, a new technique is introduced for honest classification of 7 arrhythmias from ECG signals using the fractal dimension. This method is able to identify the exact location of arrhythmias. A combination of 5 reputable universal databases is used to classify based on the fractal dimension and BPN. The performance of this method is measured by Sensitivity (SE) and Specificity (SP) indices. According to the results, the accuracy of this method is equal to 98.83%.
Keywords
Fractal dimension, Higuchi method, Combined database, ECG, Feature extraction
Fractal dimension articles, Higuchi method articles, Combined database articles, ECG articles, Feature extraction articles
Fractal dimension articles Fractal dimension Research articles Fractal dimension review articles Fractal dimension PubMed articles Fractal dimension PubMed Central articles Fractal dimension 2023 articles Fractal dimension 2024 articles Fractal dimension Scopus articles Fractal dimension impact factor journals Fractal dimension Scopus journals Fractal dimension PubMed journals Fractal dimension medical journals Fractal dimension free journals Fractal dimension best journals Fractal dimension top journals Fractal dimension free medical journals Fractal dimension famous journals Fractal dimension Google Scholar indexed journals Higuchi method articles Higuchi method Research articles Higuchi method review articles Higuchi method PubMed articles Higuchi method PubMed Central articles Higuchi method 2023 articles Higuchi method 2024 articles Higuchi method Scopus articles Higuchi method impact factor journals Higuchi method Scopus journals Higuchi method PubMed journals Higuchi method medical journals Higuchi method free journals Higuchi method best journals Higuchi method top journals Higuchi method free medical journals Higuchi method famous journals Higuchi method Google Scholar indexed journals Combined database articles Combined database Research articles Combined database review articles Combined database PubMed articles Combined database PubMed Central articles Combined database 2023 articles Combined database 2024 articles Combined database Scopus articles Combined database impact factor journals Combined database Scopus journals Combined database PubMed journals Combined database medical journals Combined database free journals Combined database best journals Combined database top journals Combined database free medical journals Combined database famous journals Combined database Google Scholar indexed journals ECG articles ECG Research articles ECG review articles ECG PubMed articles ECG PubMed Central articles ECG 2023 articles ECG 2024 articles ECG Scopus articles ECG impact factor journals ECG Scopus journals ECG PubMed journals ECG medical journals ECG free journals ECG best journals ECG top journals ECG free medical journals ECG famous journals ECG Google Scholar indexed journals Feature extraction articles Feature extraction Research articles Feature extraction review articles Feature extraction PubMed articles Feature extraction PubMed Central articles Feature extraction 2023 articles Feature extraction 2024 articles Feature extraction Scopus articles Feature extraction impact factor journals Feature extraction Scopus journals Feature extraction PubMed journals Feature extraction medical journals Feature extraction free journals Feature extraction best journals Feature extraction top journals Feature extraction free medical journals Feature extraction famous journals Feature extraction Google Scholar indexed journals BPN articles BPN Research articles BPN review articles BPN PubMed articles BPN PubMed Central articles BPN 2023 articles BPN 2024 articles BPN Scopus articles BPN impact factor journals BPN Scopus journals BPN PubMed journals BPN medical journals BPN free journals BPN best journals BPN top journals BPN free medical journals BPN famous journals BPN Google Scholar indexed journals arrhythmia articles arrhythmia Research articles arrhythmia review articles arrhythmia PubMed articles arrhythmia PubMed Central articles arrhythmia 2023 articles arrhythmia 2024 articles arrhythmia Scopus articles arrhythmia impact factor journals arrhythmia Scopus journals arrhythmia PubMed journals arrhythmia medical journals arrhythmia free journals arrhythmia best journals arrhythmia top journals arrhythmia free medical journals arrhythmia famous journals arrhythmia Google Scholar indexed journals PAC articles PAC Research articles PAC review articles PAC PubMed articles PAC PubMed Central articles PAC 2023 articles PAC 2024 articles PAC Scopus articles PAC impact factor journals PAC Scopus journals PAC PubMed journals PAC medical journals PAC free journals PAC best journals PAC top journals PAC free medical journals PAC famous journals PAC Google Scholar indexed journals
Article Details
1. Introduction
The statistics indicate that the growing number of deaths is caused by cardiovascular failures. According to the World Health Organization, about 17.3 million people died of this complication in 2008 [1]. This figure is expected to reach 23.3 million people by 2030. About 80% of death cases have occurred in countries with low or moderate per capita income, and most of them have caused by misdiagnosis or late diagnosis of the disease. Since ECG is one of the most cost-effective and accurate tools for diagnosing cardiovascular diseases, the heart behavior can be analyzed using this tool [2]. The ECG represents the electrical activity of the heart which includes the regular and calm contraction of the heart muscles. The ECG waveform analysis is a basis for the diagnosis of different cardiovascular diseases. The ECG waveform includes 5 major waves of P, Q, R, S, and T [3]. One of the most important parts of the ECG analysis is the measurement of RR-Interval and ST-segment, which are good representatives of the variety of heartbeat [4, 5]. Given the non-linear dynamism of the heart and its self-similarity features, the ECG signals present the fractal properties. As a result, the fractal dimension, which represents the non-linear dynamism, is an appropriate method for analyzing and extracting the characteristics from these signals [4, 6]. The fractal dimension indicates the ratio of minor variations in the pattern. Moreover, any system that can be imagined or analyzed geometrically is considered a fractal [7]. Hence, the fractal dimension is used to describe the fractal objects [7].
Over the last few decades, various techniques have been proposed to solve the ECG classification problems with a useful diagnosis. In most techniques, features of time [8], frequency [9], time-frequency [10], and non-linear dynamism [4, 9, 11] have been extracted and then effectively classified. Rai et al. [10] analyzed the ECG signals based on the neural network and hybrid features (Discrete Wavelet Transforms and morphological). To classify four types of arrhythmia, George and Mohammad [6] de-noised the signal and calculated the fractal dimension of the signal using Hurst Power. Sedjelmaci and Reguig [4] extracted the RR-Interval and ST-segment as a feature from each signal. Then, since the signal information is on regular change, they proposed their own method based on the regularization dimension analysis of RR-Interval and ST-segment with 4 types of arrhythmia. Martins et al. [11] used Pan-Tompkins method [12] to extract a QRS complex from the signal. Then, they de-noised the signal by the wavelet transform. Finally, they classified three types of arrhythmia using Support Vector Machin with an accuracy of 99%. Mary and Singh [13] used the DFA method to calculate the fractal dimension and detect a normal signal from an abnormal one. To categorize the natural beat of the ventricle, Mhetre et al. [8] firstly extracted the morphological features and then classified them using an expert system. Vafaie et al. [14] used a combination of neural networks and genetic algorithm to detect abnormal conditions of the heart with an accuracy of 98.67%.
After studying the methods, challenges, and shortages, a new method has been proposed in this study for classification of seven vital types of arrhythmia based on the fractal dimension. To this end, 5 reputable universal databases have been used. In the procedure of the proposed method, the signal is preprocessed in the first step. After that, considering the extracted features, the ECG signals are divided into three groups. Then, each signal is classified based on its own special features. According to the SE and SP indices, the classification accuracy is improved to 98.83%. The contributions of this paper are as follows:
- Determine the exact location of the arrhythmia occurrence and its type.
- Classification of 7 arrhythmias from ECG signals using the fractal dimension and Back Propagation Neural Network.
- The accuracy of this method was equal to 98.83%.
The rest of this paper is organized as the following: Section 2 includes the materials and methods. Section 3 deals with the fractal dimension used. Section 4 provides experimental results. Finally the paper concludes and the results are discussed in Section 5.
2. Materials and Methods
The block diagram of the proposed method has been demonstrated in Figure 1(a). As shown in Figure 1(a), the entire methodology is divided into three basic steps: preprocessing, feature extraction and classification. The preprocessing step has been shown in Figure 1(b). Different databases with different sampling frequencies have been employed in this research. In the preprocessing step, the sampling frequencies have been normalized to a base frequency that improves the speed of the algorithm and also the accuracy of the classification step. After signal frequency normalization, de-noising and Baseline wander removal of ECG signals have been done. The second step of the proposed model is feature extraction. These features must represent the original signal changes. The last step of the proposed method is dedicated to the classification of arrhythmias. Details of these steps are explained in the following sub-sections.
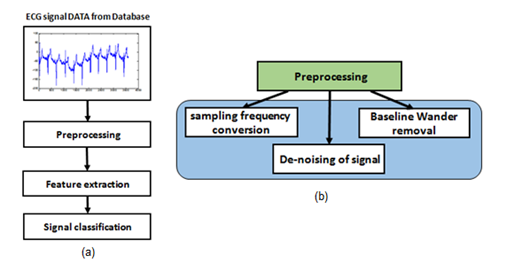
Figure 1: (a) Block diagram of proposed method of ECG analysis; (b) Block diagram of Preprocessing.
2.1 Database
Providing a proper database is one of the most important tasks of signal processing. In this research, a combination of 5 accredited databases from Physionet [15], including 321 annotated files, has been used. This database provides seven classes of arrhythmias, including Premature Ventricular Complex (PVC), Premature Atrial Contracture (PAC), Supraventricular Tachycardia (SVTA), Atrial Flutter (A_FLUT), Atrial Fibrillation (A_FIB), Ventricular Fibrillation (V_FIB) and Normal. These records are extracted from the databases listed below.
- European ST-T Database [15],
- MIT-BIH Database (Arrhythmia Database, Normal Sinus Rhythm Database, and Supraventricular Arrhythmia Database) [15],
- QT Database [15],
- Creighton University Ventricular Tachyarrhythmia Database [15],
- Intracardiac Atrial Fibrillation Database [15].
2.2 Preprocessing
Preprocessing is the first step of ECG signal processing. In this step, it is necessary to remove noise from input signals. Noise removal in the preprocessing of the ECG signal includes different strategies for each noise source [16]. Preprocessing of ECG signal consists of the sampling frequency normalization, de-noising and baseline wander removal of ECG signal (Figure 1 (b) and Figure 2). This preprocessing step must have been done before the feature extraction.
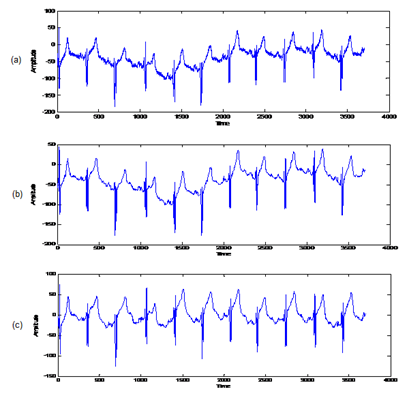
Figure 2: (a) Original or noisy ECG from database; (b) De-noised ECG signal from database; (c) Baseline wander eliminated ECG signal.
2.2.1 Sampling frequency conversion: Due to using the various databases, the first step of preprocessing is to match the frequency of signal sampling. Here, four frequencies, 128, 250, 360, and 1000 Hz, are used. Considering the mode of the frequencies and the number of the signals at each specific frequency, the frequency equal to 250 Hz is the base frequency. Sampling frequency conversion is a process which leads to changes in the sampling frequency in order to obtain a new discrete signal [17]. There are many methods to do this. In this study, Dynamic Time Warping (DTW) is used for this purpose [18]. Based on this method, the base frequency is selected and then the location of each new sample is determined. The new sample value is interpolated with regard to the previous and next points on the main signal, as shown in Equation 1. In this equation, (x0, y0) and (x1, y1) denote the points before and after the new sample on the main signal, respectively.

2.2.2 De-noising the signal: De-noising, which is done before analyzing the electrical activity of the heart, plays an important role in the processing of ECG signals [19]. The frequency band of the ECG signal varies between 0.15 Hz and 15 Hz. There are many sources of noises in the ECG signal which is placed within its frequency spectrum. In this step, the structure of different noises, including fluctuations in the heart muscle whose frequency is above 150 Hz, is removed. Since the ECG is non-stable, simple filtering operations will not be effective for de-noising [19]. Because of the proper localization of features in time and frequency domain, DWT methods have been used for this purpose in the recent studies. In this article, the de-noising method proposed by the authors [20] are used in order to overcome the problem of DWT variance changes and maintain the physiological characteristics of the signal. In this algorithm, the signal is divided into 9 levels using the Dual-Tree Complex Wavelet Transform. Threshold values are calculated using the DF factor and then applied to the first two levels. Thresholding of other levels is done using the Donoho thresholding method [21]. The threshold of each level is applied to partial coefficients by soft-thresholding. Then, the signal is reconstructed using modified partial coefficients. Details of the parameters are as the following:
- Donoho method λ=√2logM) where M shows the value of coefficients [21].
- DF Factor in any sub-band of J is calculated as follows:

Where, FjSN, µ, and σ2 represent ratio signal kurtosis value in j band to kurtosis value of the signal, mean of partial coefficients, and variance of partial coefficients. In addition, djk denotes the wavelet coefficients under the band J [22].
- In soft-thresholding, all coefficients are modified or converted into zero with regard to the threshold λ, and a fraction of λ value is considered as the noise value.

2.2.3 Baseline wander removal: Noise artifacts that affect the ECG signal are called Baseline Wander. Regularly, these noises are in the range of 0.15 to 0.3 Hz and enter the signal using a breathing apparatus. Baseline Wander removal reduces the heartbeat irregularities in the ECG analysis. There are different ways to remove Baseline Wander from the signal. In this study, the method proposed by Rai et al. [10] are used. After removing the signal noises by moving the average filter, the signal is smoothed. The results are then plotted in the column vector y. To smooth the data, a step size of 200 is used to produce better results. After smoothing, the difference between the smoothed signal and the initial signal are calculated. As a result, the signal obtained is empty of any Baseline Wander.
2.3 Feature extraction
In this step, extracted features are evaluated based on the fractal dimension. In this study, new and accurate features are calculated using the fractal dimension. Various methods for the calculation of the fractal dimension, including Katz, Box Counting, Higuchi, Hurst, Regularization, DFA, Sevcike, and PSD have been investigated that the Higuchi method can better show the changes and disease in the ECG signal. In addition, this method can examine a variety of patients more powerfully.
2.3.1 Local-FD and Max-ST: After passing the preprocessing stage, a window of 10 seconds is passed over the signal without overlapping. Since this feature indicates different arrhythmias, the detection speed is accelerated using the window of 10 seconds. Then, the Higuchi dimension is calculated for each window. Finally, the difference of both consecutive values is calculated. The highest value represents this feature. To calculate the Max-ST, the R peaks are identified and then the ST-segment value is calculated. This can be done through various methods which are generally divided into 3 major categories that the first method is the quickest one. In the present study, Pan-Tompkins method [12] is used. Although this method is more complex than its counterparts, it is one of the most accurate and widely used methods. The maximum ST-segment value represents Max-ST.
2.3.2 Average-FDH: When the R peaks are identified by Pan-Tompkins method, the fractal dimension in relation to the distance between the two peaks is calculated using Higuchi method. Then, the mean of these values is introduced as the Average-FDH.
2.3.3 Npac, Npvc and Npsvt: The purpose of these features is to identify peaks that are likely to cause illness. After calculating RR-Interval, the signals with a RR-Interval of greater than 0.2 seconds are diagnosed suspected to illness. In arrhythmias that occur only in some peaks, there would be a long after any peak of disease. The fractal dimension related to RR-Interval is calculated using Higuchi method. Since it has been shown that the heart has a nonlinear system, more severe diseases have a smaller fractal dimension. According to the results, susceptible peaks can be classified into four groups with regard to the fractal dimension.
Normal: FD >1.56
PAC: 1.37 < FD ≤ 1.56
PVC: 1.3 < FD ≤ 1.37
PSVT: 1 < FD ≤ 1.3
Then, susceptible peaks that are diagnosed normal will be removed. The number of peaks related to each of the PAC, PVC, and PSVT will be sent to the output as Npac, Npvc, and Npsvt features.
2.4 Signal classification
As shown in Figure 3, there are three groups of arrhythmias in this combined database. The first group includes arrhythmias that occur in some peaks, such as PAC, PVC, and PSVT. The second group involves A-FLUT and A-FIB that influence the whole signal. Finally, the third group includes arrhythmias that occur suddenly and continue. V-FIB is an example of this group in which the heart rate is normal, but suddenly becomes similar to ventricular fibrillation/flutter. In the proposed algorithm, after the entry of the signal and passing through the previous two steps, local-FD is firstly calculated and then V-FIB arrhythmia is detected (Figure 4). In V-FIB, the heart signal is normal at first and then suddenly the rhythm of the heart becomes extremely swirling, as the ECG signal peaks cannot be detected. Therefore, local-FD is a good benchmark for diagnosing this type of disease which occurs suddenly and continues. A local-FD of greater than 1.5 is an indication of V-FIB arrhythmia. In the next step, A-FIB and A-FLUT are separated. These two types of arrhythmia have a sharp rhythm in the whole signal. In addition, the heart rate is very high. For classification, Max-ST is extracted from the signal. Since the peaks are close to each other, Max-ST value here is much smaller than the other arrhythmias. As a result, a Max-ST smaller than 100 indicates one of these two arrhythmias. However, if the signal is in this category, A-Fib and A_FLUT arrhythmias are separated in the second step by using a trained BPN with Average-FDH and Max-ST features. In this step, the first type of arrhythmias is diagnosed that basically occur as single peaks. Features, including the Average-FDH, Npac, Npvc, Npsvt, and Max-ST, are extracted from the signal and the disease is diagnosed using Algorithm 1.
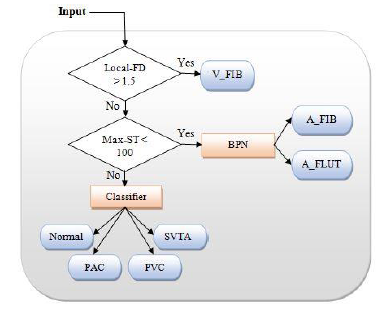
Figure 3: Combining Database.
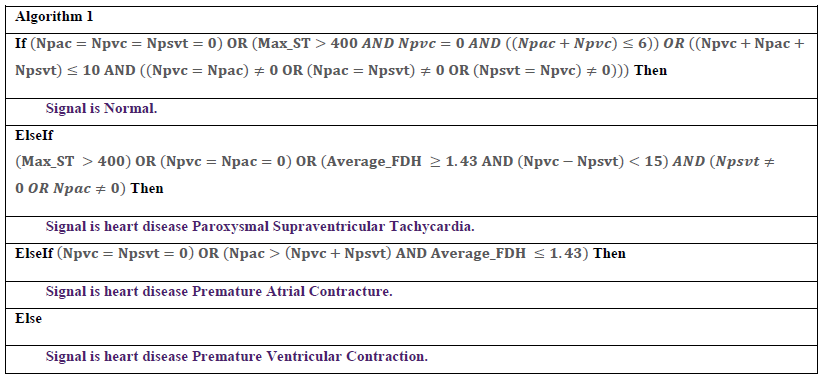
Figure 4: Block diagram of signal classification method.

3. Fractal Dimension
There are different algorithms for calculating the Fractal Dimension, such as Katz [23], box-counting [24], Higuchi [25], Regularization [26], and etc. Each of them has its own advantages and disadvantages. In this research, these methods have been studied and reviewed. It has been included that Higuchi is an accurate method and a good representative of disease. The Higuchi algorithm has the property of intrinsic repeatability as same as the box-counting method. Assume time series of x={x(1), x(2), …, x(N)}, the Fractal Dimension is calculated as follows.

4. Experimental Results
In this paper, the experiments have been carried out in MATLAB software package 11. The hybrid database consists of 321 records that have been divided into 7 separate classes: PAC, PVC, SVTA, A_FLUT, A_FIB, V_FIB and Normal. 10 minutes of each file has been considered and analyzed. For those arrhythmias, which are shorter than 10 minutes, the shorter amount of time has been considered and analyzed. All features are divided into two groups: fractal dimension features and morphologic features of ECG signal. While the Max-ST is a morphologic feature, the Local-FD, Average-FDH, Npac, Npvc and Npsvt are fractal features of the signal. In this research, the signal classification has been done according to these features by using a BPN with 20 neurons in the hidden layer and a MLP classifier with 10 neurons in its hidden layer. In order to train mentioned networks, 70% of data is used as the training data and the remained 30% of data as the test data. The simulation results demonstrate that BPN with 20 neurons in hidden layer achieves the best results (Table 1 and Figure 5). Thus, in this research, a BPN has been used to classify A_FLUT and A_FIB using Average-FDH and MAX_ST.
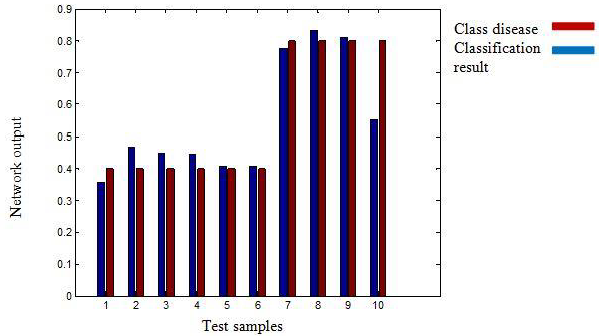
Figure 5: performance chart of BPN.
|
Accuracy (%) |
Number of correct classification |
Number of neurons |
Methods |
||||
|
Testing Data |
Training Data |
Testing Data |
Training Data |
||||
|
100 |
95 |
10 |
21 |
10 |
BPN |
||
|
100 |
100 |
10 |
22 |
20 |
|||
|
90 |
95 |
9 |
21 |
10 |
MLP |
||
|
90 |
100 |
9 |
22 |
20 |
|||
|
SP (%) |
SE (%) |
Number of correct classification |
|||||
|
Total |
A_FIB |
A_FLUT |
|||||
|
94 |
100 |
31 |
16 |
15 |
10 |
BPN |
|
|
100 |
100 |
32 |
16 |
16 |
20 |
||
|
87 |
100 |
30 |
16 |
14 |
10 |
MLP |
|
|
100 |
94 |
31 |
15 |
16 |
20 |
||
Table 1: Compare the performance of MLP and BPN.
The performance of the classifier has been evaluated by using the most familiar metrics: SE and SP [27].

Where TP is the number of true positive samples, TN is the number of true negative samples, and FN is the number of positive samples. The most important metric for evaluating the overall system performance is usually accuracy [27]:

|
Accuracy |
98.83% |
|
SE |
99.74% |
|
SP |
96.84% |
Table 2: The results of classification using the proposed algorithm.
|
SE and SP |
Normal |
PVC |
PSVT |
PAC |
A_FIB |
AF |
V_FIB |
|
SE |
99.1 |
100 |
99.1 |
100 |
100 |
100 |
100 |
|
SP |
100 |
100 |
97.9 |
80 |
100 |
100 |
100 |
Table 3: The comparison between SE and SP from each class according to the proposed algorithm.
Table 2 shows the results of classification using those features which have been extracted based on the fractal dimension. This classification of 7 classes has been achieved the precision of 98.83%. Table 3, shows the calculation of SE and SP for each class in comparison to each other. PVC, A_FLUT, A_FIB and V_FIB have been completely separated with SE=100 and SP=100; so, fractal dimension is an appropriate representative of them. SE and SP for the Normal class are 99.1 and 100, respectively. Thus, it has been separated perfectly as well; however, in some cases, other arrhythmias have been incorrectly detected as Normal. SE=100 and SP=80 for PSVT class demonstrate that sometimes the disease associated with PSVT class is diagnosed incorrectly. Finally, SE and SP for PAC class are 99.1 and 97.9, respectively. It shows that the proposed algorithm is less sensitive at the boundary of this disease. Therefore, the proposed algorithm has some sensitivity at the boundary of diagnosis of Normal and PAC diseases and also at the boundary of diagnosis of PAC and PSVT diseases.
5. Discussion and Conclusion
The main objective of this study was to classify a variety of hazardous arrhythmias with high accuracy based on a wide variety of disease-rich databases. In most studies, a maximum of four arrhythmias is classified with a limited number of files. In this study, seven types of arrhythmias were classified using a combined database, including a sufficient number of files. In this paper, a new method based on the fractal dimension of the ECG signal was proposed which is the best representative of the electrical activity of the heart, with regard to the chaotic system of the heart. The fractal dimension is able to examine minor changes in complex signals. The proposed algorithm is able to determine the exact location of the arrhythmia occurrence and its type. In the proposed method, the signal was preprocessed in three steps and the features were extracted based on the fractal dimension and morphological characteristics of the signal. Then, classification was done based on extracted features. The performance of this method was measured by SE and SP indices. According to the results, the accuracy of this method was equal to 98.83%. Increasing the accuracy and the number of arrhythmias under study can be good recommendations for future studies.
Conflict of Interest
The authors claim that they do not have conflict of interest.
Acknowledgment
During this study, we also would like to demonstrate our appreciation to the physio bank for sharing databases of heart disease and biometric signals.
References
- Mendis S, Puska P, Norrving B. World Health Organization. Global atlas on cardiovascular disease prevention and control. Geneva: World Health Organization (2011).
- Kirk KJ, O’Shea J, Ruhf LK. ECG interpretation made incredibly easy!. Chris Burghardt. 5 (2011).
- Maglaveras N, Stamkopoulos T, Diamantaras K, et al. ECG pattern recognition and classification using non-linear transformations and neural networks: A review. International journal of medical informatics 1-3 (1998): 191-208.
- Sedielmaci I, Reguig FB. Detection of some heart diseases using fractal dimension and chaos theory. In 2013 8th International Workshop on Systems, Signal Processing and their Applications (WoSSPA) 1 (2013): 89-94.
- Castiglioni P, Faini A, Lombardi C, et al. Characterization of apnea events in sleep breathing disorder by local assessment of the fractal dimension of heart rate. In2014 8th Conference of the European Study Group on Cardiovascular Oscillations (ESGCO) 8 (2014): 107-108.
- Oweis R, Hijazi L. A computer-aided ECG diagnostic tool. Computer methods and programs in biomedicine 3 (2006): 279-284.
- George JJ, Mohammed EM. Heart disease diagnostic graphical user interface using fractal dimension. In 2013 International Conference on Computing, Electrical and Electronic Engineering (ICCEEE). 1 (2013): 336-340.
- Pipberger HV, Arms RJ, Stallmann FW. Automatic Screening of Normal and Abnormal Electrocardiograms by Means of a Digital Electronic Computer. Proceedings of the Society for Experimental Biology and Medicine 1 (1961): 130-132.
- Addison P. Fractals and Chaos. Napier University, Edinburgh (1997).
- Mhetre MR, Vaishampayan A, Raskar M. ECG Processing & Arrhythmia Detection: An Attempt. International Journal of Engineering and Innovative Technology (IJEIT) 2 (2013): 272-276.
- Ebrahimzadeh E, Pooyan M, Bijar A. A novel approach to predict sudden cardiac death (SCD) using nonlinear and time-frequency analyses from HRV signals 2 (2014): e81896.
- Rai HM, Trivedi A, Shukla S. ECG signal processing for abnormalities detection using multi-resolution wavelet transform and Artificial Neural Network classifier. Measurement 9 (2013): 3238-3246.
- Martis RJ, Acharya UR, Min LC. ECG beat classification using PCA, LDA, ICA and discrete wavelet transform. Biomedical Signal Processing and Control 5 (2013): 437-448.
- Spasi? S, Savic A, Nikolic L, et al. Applications of Higuchi’s fractal dimension in the Analysis of Biological Signals. In2012 20th Telecommunications Forum (TElFOR) 1 (2012): 639-641.
- Pan J, Tompkins W. A real-time QRS detection algorithm. IEEE Transaction on biomedical Engineering 3 (1985): 230-236.
- Mary HM, Singh D. Fractal dimension of electrocardiogram: distinguishing healthy and heart-failure patients. Journal of Electrocardiology 1 (2013): e21-e37.
- Vafaie MH, Ataei M, Koofigar HR. Heart diseases prediction based on ECG signals’ classification using agenetic-fuzzy system and dynamical model of ECG signals. Biomedical Signal Processing and Control 1 (2014): 291-296.
- Kumar G, Kumaraswamy YS. Spline activated neural network for classifying cardiac arrhythmia 8 (2014): 1582-1590.
- Physiobank archive index.
- Rai HM, Trivedi A. De-noising of ECG waveforms using multiresolution wavelet transform. International Journal of Computer Application 18 (2012): 25-30.
- Oppenheim AV, Schafer RW. Discrete-Time Signal Processing 3 (2011): 1120.
- Rabiner LR, Schafer RW. Introduction to Digital Speech Processing. Inc, Hanover (2007): 200.
- Kania M, Fereniec M, Maniewski R. Wavelet denoising for multi-lead high resolution ECG signals. Measurement science review 4 (2007): 30-33.
- Raj VN, Venkateswarlu T. ECG signal denoising using undecimated wavelet transform. In2011 3rd International Conference on Electronics Computer Technology 1 (2011): 94-98.
- Maghsoudi F, Kiani K. A powerful novel method for ECG signal de-noising using different thresholding and Dual Tree Complex Wavelet Transform. the 2th Int. Knowledge-Based Engineering and Innovation (2015).
- Donoho DL, Johnstone IM. Adapting to unknown smoothness via wavelet shrinkage. Journal of the american statistical association 1 (1995): 1200-1224.
- Sharma LN, Dandapat S, Mahanta A. ECG signal denoising using higher order statistics in Wavelet subbands. Biomedical Signal Processing and Control 1 (2010): 214-222.


 Impact Factor: * 4.2
Impact Factor: * 4.2 CiteScore: 2.9
CiteScore: 2.9  Acceptance Rate: 11.01%
Acceptance Rate: 11.01%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 