Biomechanical Analysis of Jaw Bone with Cyst Using CT-Image Based Finite Element Method
Takaaki Arahira1, Mitsugu Todo2*
1Department of Dental Engineering, Fukuoka Dental College 2-15-1 Tamura, Swara-ku, Fukuoka 814-0193, Japan
2Research Institute for Applied Mechanics, Kyushu University 6-1 Kasuga-koen, Kasuga 816-8580, Japan
*Corresponding Author: Mitsugu Todo, Research Institute for Applied Mechanics, Kyushu University 6-1 Kasuga-koen, Kasuga, Fukuoka 816-8580, Japan
Received: 08 May 2018; Accepted: 16 May 2018; Published: 18 May 2018
Article Information
Citation: Takaaki Arahira, Mitsugu Todo. Biomechanical Analysis of Jaw Bone with Cyst Using CT-Image Based Finite Element Method. Dental Research and Oral Health 1 (2018): 007-010.
View / Download Pdf Share at FacebookAbstract
A three-dimensional jaw bone model consisting of maxilla and mandible was constructed using CT- images. The distribution of Young’s modulus was also estimated from the bone density distribution. The developed model was then applied to analyze the effect of a spherical cyst located in the mandible on the mechanical condition in the jaw bone using the finite element method. An occlusion condition was used as the boundary condition by employing muscle forces. It was found that the strain energy density was concentrated in the several regions in the vicinity of the cyst, and the regions were generated by both tensile and compressive stress concentrations. It is thus concluded that this kind of 3-D modeling could clinically be used for predicting the risk of fracture of jaw bones.
Keywords
<p>Dental biomechanics; CT-image based modeling; Occlusion; Finite element analysis</p>
Article Details
1. Introduction
CT-image based modeling has been developed to construct realistic bone models with their 3-D shape and structure and has effectively been applied to clinical problems in the fields of orthopedics and dental science [1-9]. In this modeling technique, a 3-D bone model is constructed from a series of CT-images by extracting the cross-sectional areas corresponding to the bone. Recently, the concentration of CT-value on the CT-images is successfully used to estimate the density of the bone and furthermore, the corresponding Young’s modulus [6-9].
In the field of dental science, simplified bone models have mainly been used to analyze clinical problems, for example, the mechanical interaction between the bone and dental implants [10-13]. Recently, full mandible or maxilla models have been constructed using CT-images in order to assess the effect of complete bone structure on the mechanical condition [1-5]. However, such mandibular models are still far from the real structure of jaw bone that consists of maxilla and mandibular bones. Dental occlusion can be achieved by the contact process between the two bones and therefore, it is ideal that full jaw bone model is used to analyze the stress state during occlusion process. However, a few attempts have been made to develop such jaw bone models using CT-images.
Cyst is a disease that directly affects tissue of jaw bones, and constructed by antrum with liquid constituent inside [14, 15]. A CT-image of a typical example of cyst generated in a mandibular bone is shown in Figure 1. Existence of such cyst in a mandible causes disturbance of the teeth nearby and furthermore, fracture of the mandible could occur when the surrounding cortical bone becomes very thin as the cyst grows. It is therefore clinically important to understand the mechanical condition of jaw bone with cyst under a circumstance of occlusion in order to assess the risk of fracture.
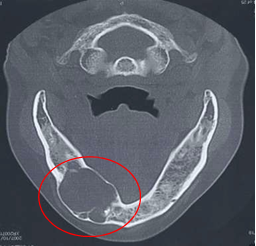
Figure 1: Cyst developed in a mandibular bone.
In this study, therefore, a three-dimensional finite element model of a female jaw bone consisting of maxilla and mandible was developed by using CT-images. Distribution of Young’s modulus was also considered by using a theoretical relationship between bone density and Young’s modulus. An ideal spherical cyst model was then introduced into the mandible of the jaw bone model. Boundary conditions for an occlusion was assigned to each of the models and then finite element analysis was performed to assess the concentration patterns of strain energy density and maximum and minimum principal stress values in the vicinity of the cyst. The risk of fracture was then discussed on the basis of the computational results.
2. Development of Finite Element Models
A series of X-ray CT images of a 23 years old female was used to construct a computational jaw bone model. The number of the images was 100, and the slice distance was 1 mm. Mechanical Finder, a software for finite element modeling and analysis of bone structure, was used in this study. From each of the CT images, parts of bone and teeth were extracted automatically by setting a threshold value. Maxilla and mandible models were then constructed separately by accumulating the related parts of bone and teeth. The upper part of the maxilla from the center of the cavity of nose was omitted and also, soft tissues such as periodontal membrane were not considered in this modeling. 4 nodes tetrahedra elements were used to construct finite element models of the jaw bone and the total numbers of elements and nodes were 880899 and 188230, respectively. The 3-D computational model and the finite element model of the jaw bone were shown in Figure 2.
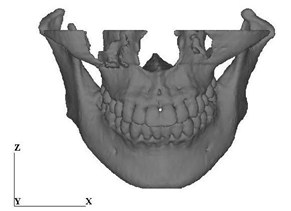
Figure 2: CT-image based jaw bone model. (a) Jawbone model

Figure 2: CT-image based jaw bone model. (b) Mesh image
The bone density, r, corresponding to an element was estimated from the CT value using the following formula [6]:
r (g/cm3) = (CT value + 1.4246)×0.001/1.0580 for CT value > -1 (1)
r (g/cm3) = 0.0 for CT value≤-1 (2)
Then, the Young’s modulus of the element was calculated from the corresponding bone density by using the Keyak’s theory shown in Table 1 [6].
|
Bone density [g/cm3] |
Young’s modulus [MPa] |
|
r = 0 |
E=0.001 |
|
0 |
E=33900 r 2.20 |
|
0.27 < r <0.6 |
E=5307r +469 |
|
0.6?r |
E=10200r 2.01 |
Table 1: Convert density into young’s modulus.
An ideal cyst with spherical shape was introduced into the mandibular model. The diameter of the cyst was chosen to be 4 and 8 mm. The Young’s modulus and the Poisson’s ratio of the cyst were assumed to be 0.1 Pa and 0.3. The cyst was completely connected to the surrounding bone. The locations of the cyst within the jaw bone model are shown in Figure 3.
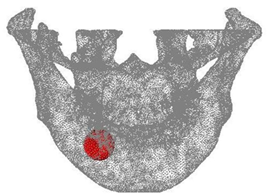
Figure 3: Location of the spherical cyst model.
Mechanical boundary condition is shown in Figure 4(a). Occlusion was reproduced by employing the mechanical condition proposed in Reference 14. Muscular forces were applied to the condylar and coronoid processes considering the directions of the muscles. Five different muscular forces such as masseter, anterior temporalis, posterior temporalis, medial pterygiod and lateral pterygiod were considered in this modeling, and the resultant of the muscular forces was about 200 N. Restraint condition is shown in Figure 4(b). The top of the maxilla was totally fixed. The top of the right condylar process was also totally fixed and the top of the left condylar process was allowed to move only in the x-direction. The top surfaces of the teeth of the mandible contact to those of the maxilla without friction.
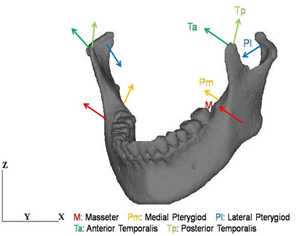
Figure 4: Boundary conditions. (a) Mechanical condition.
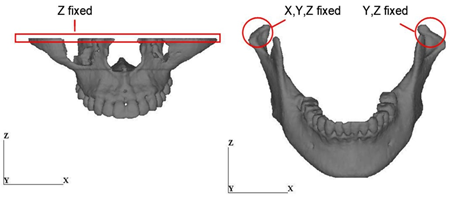
Figure 4: Boundary conditions. (b) Restraint condition
3. Results and Discussion
3.1 Distribution of Young’s modulus
The distributional patterns of Young’s modulus on the frontal surface and the central cross-section are shown in Figure 5. The highest modulus corresponds to the enamel of the teeth. It is also clearly seen from the cross-sectional view that the regions of the higher and the lower modulus correspond to the cortical bone and the cancellous bone, respectively.
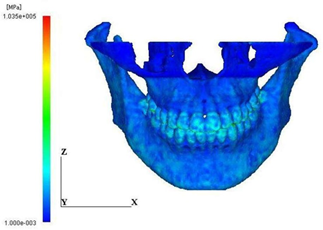
Figure 5: Distribution of young’s modulus. (a) Anterior view
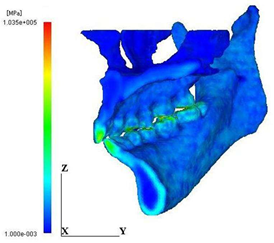
Figure 5: Distribution of young’s modulus. (b)Lateral view
3.2 Distribution of strain energy density and principal stress
The distribution patterns of strain energy density for the normal model and the cyst model are shown in Figure 6. It is obviously seen that the concentration of the strain energy density in the cortical bone surrounding the cyst is more extensive and higher than that in the normal model. The cyst covered 90% of the cross-section and therefore, the thickness of the surrounding cortical bone became very thin, resulting in such high energy concentration. The maximum values of the strain energy density within the region surrounding the cyst are shown in Figure 7. It should be noted that the maximum value increased with increase of the cyst diameter and the maximum value for the largest cyst is thirteen times larger than that for the normal.
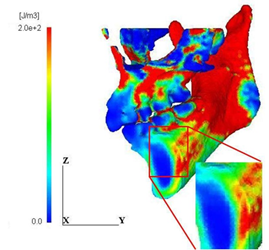
Figure 6: Distribution of strain energy density. (a) Normal model
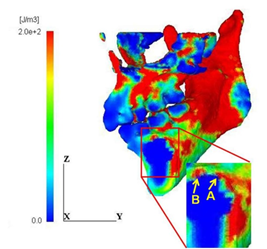
Figure 6: Distribution of strain energy density. (b) Cyst model
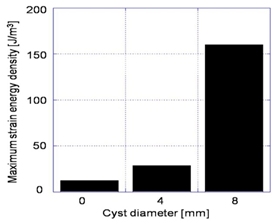
Figure 7: Effect of cyst size on strain energy density.
The maximum and the minimum principal stress distributions are shown in Figure 8. It is noted that the regions A and B of high energy concentration shown in Figure 6(b) correspond to the maximum stress concentration region A in Figure 8(a) and the minimum stress concentration region B in Figure 8(b), respectively. It is thus understood that such energy concentration regions were generated by both high tensile and compressive stress concentration in the vicinity of the cyst. In general, the tensile strength of bone is much lower than the compressive strength; therefore, the initiation of fracture of the mandible with the cyst is likely to take place at the point A.
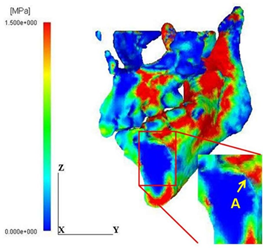
Figure 8: Distribution patterns of principal stress values. (a) Maximum principal stress
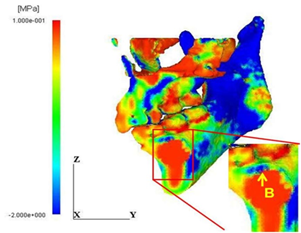
Figure 8: Distribution patterns of principal stress values. (b) Minimum principal stress
The mechanical boundary condition used in this study imitated a simple occlusion condition with moderate forces, therefore, the stress level may not be so severe one that causes fracture of the mandible. In order to apply the developed model to the prediction of such fracture problems, more severe mechanical boundary conditions that imitate, for example, falling down and impact of foreign object need to be considered.
4. Conclusions
3D finite element model of a jaw bone with cyst was developed using CT-images. Young’s modulus distribution was also considered by using bone density distribution estimated from the CT values. Stress analysis was then performed in order to assess the effect of cyst on the concentrations of strain energy density and principal stress values. The conclusions are summarized as follows:
- A computational jaw bone model consisting of maxilla and mandible was successfully developed using CT-images.
- A distribution pattern of Young’s modulus was obtained from the bone density distribution estimated by using CT values.
References
- Akca K, Iplikcioglu H. Finite element stress analysis of the effect of short implant usage in place of cantilever extensions in mandibular posterior edentulism. Journal of Oral Rehabilitation 29 (2002): 350-356.
- Ziebowicz A, Marciniak J. The use of miniplates in mandibular fractures: biomechanical analysis. Journal of Materials Processing Technology 175 (2006): 452-456.
- Reimann S, Keiling L, Jager A, et al. Biomechanical finite-element investigation of the position of the centre of resistance of the upper incisors. European Journal of Orthodontics 29 (2007): 219-224.
- Daas M, Dubois G, Bonnet AS, et al. A complete finite element model of a mandibular implant-retained overdenture with two implants: Comparison between rigid and resilient attachment configurations. Medical Engineering Physics 30 (2008): 218-225.
- Boccaccio A, Prendergast PJ, Pappalettere C, et al. Tissue differentiation and bone regeneration in an osteotomized mandible: a computational analysis of the latency period. Medical and Biological Engineering and Computing 46 (2008): 283-298.
- Keyak JH, Rossi SA, Jones KA, et al. Prediction of femoral fracture load using automated finite element modeling. Journal of Biomechanics 31 (1998): 125-133.
- Reina JM, Garcia-Aznar JM, Dominguez J, et al. Numerical estimation of bone density and elastic constants distribution in a human mandible. Journal of Biomechanics 40 (2007): 828-836.
- Ong KL, Kurtz SM, Manley MT, et al. Biomechanics of the Birmingham hip resurfacing arthroplasty. Journal of Bone and Joint Surgery - Series B 88 (2006): 1110-1115.
- Teoh SH, Chui CK. Bone material properties and fracture analysis: Needle insertion for spinal surgery. Journal of the Mechanical Behavior of Biomedical Materials 1 (2008): 115-139.
- Petrie CS, Williams JL. Probabilistic analysis of peri-implant strain predictions as influenced by uncertainties in bone properties and occlusal forces. Clinacal Oral Implant Reserch 18 (2007): 611-619.
- Meyer U, Vollmer D, Punte C, et al. Bone loading pattern around implants in average and atrophic edentulous maxillae: a finite-element analysis. Journal of Cranio- Maxillofacial Surgery 29 (2001): 100-105.
- van Rossen IP, Break LH, de Putter C, et al. Stress-absorbing elements in dental implants. Journal of Prosthetic Density 64 (1990): 198-205.
- Sertgoz A, Guvener S. Finite element analysis of the effect of cantilever and implant length on stress distribution in an implant-supported fixed prosthsis. The Journal of Prosthetic Dentistry 76 (1996): 165-169.
- Inou N, Fujiwara H, Maki K. 3-D FE Stress Analyses of Mandibular during biting. Transactions of the JSME Series A 58 (1992): 1042-1045.


 Impact Factor: * 3.1
Impact Factor: * 3.1 Acceptance Rate: 76.66%
Acceptance Rate: 76.66%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 