A Modified Compartmental Pharmacokinetic Model of Enterohepatic Circulation for Simvastatin in Healthy Mexican Subjects. A Pilot Study
Melchor Alpízar-Salazara*, Miguel Alejandro Trejo-Rangela, José de Jesús Reséndiz-Rojasa, Tamara Daniela Frydmana, Carlos Ramos-Mundob
aSpecialized Centre for Diabetes, Obesity and Prevention of Cardiovascular Disease (CEDOPEC, S.C.). 3rd Street #7, Reforma Social, Miguel Hidalgo, Mexico City, 11650, Mexico
bChemical Science Department, La Salle University. Benjamín Franklin Avenue #45, Condesa, Cuauhtémoc, Mexico City, 06140, Mexico
*Corresponding Author: Melchor Alpízar-Salazar, MD, PhD, FACE, Specialized Centre for Diabetes, Obesity and Prevention of Cardiovascular Disease (CEDOPEC, S.C.). 3rd Street #7, Reforma Social, Miguel Hidalgo, Mexico City, 11650, Mexico, Tel: +525552825400, ORCID: https://orcid.org/0000-0003-2033-481X;
Received: 21 October 2020; Accepted: 03 November 2020; Published: 17 November 2020
Article Information
Citation: Melchor Alpízar-Salazar, Miguel Alejandro Trejo-Rangel, José de Jesús Reséndiz-Rojas, Tamara Daniela Frydman, Carlos Ramos-Mundo. A Modified Compartmental Pharmacokinetic Model of Enterohepatic Circulation for Simvastatin in Healthy Mexican Subjects. A Pilot Study. Journal of Pharmacy and Pharmacology Research 4 (2020): 103-115.
View / Download Pdf Share at FacebookAbstract
Enterohepatic circulation (EHC) is a process that many drugs go through, in which, after extravascular administration, they are absorbed in the intestine, secreted in the bile and then reabsorbed during one or more circulation cycles that alter plasmatic concentrations of said drugs. The aim of this study was to compare a new pharmacokinetic model of EHC with the classic model of extravascular administration after administering Simvastatin. A single-center, randomized, controlled, prospective, longitudinal, single-dose, cross-over study was performed with a 7-day washout period, in healthy Mexican subjects. The plasma samples obtained were quantified with HPLC-MS / MS using a validated analytical method. Cmax, tmax, AUC0-24h and AUC0-∞ were determined, and both models were compared with the Akaike Information Criterion (AIC) and r^2. Results show that the pharmacokinetic parameters calculated with the EHC model are fairly similar to those obtained with the trapezoidal model, even more so than those obtained with the classic model. The AIC and r^2 criteria were lower for the EHC model (AIC=11.256 and 12.555, r^2=0.568 and 0.440) vs the classic model (AIC=9.382 and 9.195, r^2= 0.884 and 0.922). In conclusion, a new pharmacokinetic model for EHC was developed, and results confirmed that it adjusts well to experimental data, offering an alternative way to calculate Cmax, tmax and AUC0-t, and can also be adapted to other drugs that exhibit EHC as well.
Keywords
Enterohepatic circulation (EHC); Pharmacokinetics; Pharmacokinetic model; Simvastatin
Enterohepatic circulation (EHC) articles; Pharmacokinetics articles; Pharmacokinetic model articles; Simvastatin articles
Article Details
1. Introduction
Enterohepatic circulation (EHC) of bile acids is a secretion and recapture process that begins with bile acid excretion from the liver, followed by intestine absorption towards portal circulation, ending up in the liver to restart the same cycle [1,2]. Although EHC of endogenous compounds occurs mainly for bile acids, it can also take place for hormones such as estrogen [3], thyroxine (T4) and triiodothyronine (T3) [4]; vitamin D [5], folate [6] and insulin-like growth factors (IGF) [7].
There are also reports of drugs that are subject to EHC [8]. The most important change caused by EHC in a pharmacokinetic profile can be found in the area under the curve (AUC) of plasma concentration [9], which is depicted as multiple peaks in concentration vs time, also known as “the sawtooth effect” [10]. Several articles have discussed the impact that EHC can have on pharmacokinetics [11–15]. From a clinical standpoint, EHC can modify the pharmacological effect by altering plasmatic concentration [16].
Several models have been considered to explain the EHC process studied for certain drugs. These models are generally compartmental and can be classified by their general characteristics in: simple two compartment models [17,18], compartmental models based on gallbladder emptying start time (Tgap) [19,20], continued release models [21], single release models [22–24], and multiple release models through switch function [25], by sigmoid function [26] or by sinusoidal function [27]. Recently, these compartmental models have been studied to describe their advantages and disadvantages [28]. This paper displays a different approach by an inclusion of parameters in an empirical function to be able to modify the profile and achieve a double peak representation of concentration through time, thereby sticking to the exponential function values. In any case, these models should be tested with volunteered data from experimental studies using drugs that have EHC.
Among drugs that show EHC is Simvastatin, a lipid lowering drug derived from microbial products (through Aspergillus terreus fermentation), which once hydrolyzed to its active state, competitively inhibits the 3-hydroxi-methylglutaryl coenzyme A reductase (HMG-CoA), thus avoiding its conversion to mevalonate, a limiting step in cholesterol´s biosynthesis [29]. This project aims to apply and evaluate adequacy of a mathematical model that describes the pharmacokinetics of Simvastatin with EHC in healthy Mexican subjects.
2. Material and Methods
This research study was conducted in compliance with the Mexican Official Norm NOM-177-SSA1-2013 [30] and was approved by a research and an ethics committee, as well as the regulatory authority, COFEPRIS, which ensures that international ethical standards for clinical research were met.
The reference drug used in this study was Simvastatin 20 milligram tablet (Zocor®, Merck Sharp & Dohme, Drug A) and the trial drug was a similar formulation, fabricated by Kener Laboratories (Drug B). Both products were analyzed and approved in accordance with the Mexican pharmacopoeia (FEUM).
The following inclusion criteria were met for subject recruitment: 18-55 years old, 18-27 kg/m2 Body Mass Index (BMI), complete clinical history with no relevant findings, normal routine blood work (less than 3 months old). Exclusion criteria included recent illness, alcohol or drug abuse history, smokers, concomitant medications, pregnancy, recent hospitalization, or loss of 450 mL of blood. A total of 8 subjects were included, 5 men and 3 women. The two drugs were randomly assigned. Elimination causes were defined as consent form withdrawal, serious adverse events or adverse events that could interfere with the pharmacokinetics.
A longitudinal, prospective, cross-randomized, single blind study was performed which consisted of two treatments administered during two periods of time (2x2), in fasting conditions. This was carried out in E-BIOS-CEDOPEC, Mexico City. The drugs were administered in a single dose per period with 250 milliliters of water. There was a washout time of 7 days between periods.
Both periods consisted of the same process (described below), and after the second period, the subjects were asked to come back 3 days later for a follow-up assessment and to end their participation.
During each period, a catheter was placed on the subject arm to collect blood samples at baseline (pre-dose), 0.5, 0.75, 1.0, 1.25, 1.50, 1.75, 2.0, 2.25, 2.50, 2.75, 3.0, 3.5, 4.0, 5.0, 6.0, 9.0, 12.0 and 24 hours after drug administration. All samples were extracted onto heparinized tubes. Immediately afterwards, the tubes were centrifuged at 4000 rpm for 15 minutes at room temperature to separate the plasma. Then, they were placed in deep freezing (-70°C). After both periods had passed, the samples were delivered to the Analytical Unit.
The plasma samples were quantified by a High Performance Liquid Chromatography (HPLC) validated method with equipment coupled to Tandem Mass Spectrometry (MS-MS), with a Zorbax eclipse XDB-C18 column, 2.1 x 50 mm, 5 µm, with mobile phase of formic acid 10 mM: MeOH (20:80 v/v), at a flow rate of 0.3 mL/min. Sibutramine was used as an internal standard (IS). The mass/load ratio for Simvastatin was 441.36>325.41 and 280 >125 for the IS. To extract the Simvastatin from the plasma, a liquid-liquid technique was used with an extraction solution of ether: hexanes 80:20 v/v. This method was validated by the Analytical Unit in compliance with the NOM-177-SSA1-2013.
The main pharmacokinetic parameters (tmax, Cmax, AUC0-24h and AUC0-∞) were obtained for each subject through the quantification of Simvastatin plasma concentration. AUC0-24h was calculated by the trapezoidal method, while the AUC from the last measurable concentration to infinity was calculated with the terminal phase slope assuming that this phase followed a monoexponential profile. Afterwards, the descriptive statistics were obtained for each drug using the arithmetic average and standard deviation. Using the analysis of variance for Cmax, AUC0-24h and AUC0-∞ logarithms, the intrasubject variance coefficients were determined. This was carried out using SPSS v22. Cmax, tmax, AUC0-24h and AUC0-∞ were determined from the mean profiles, the EHC model and the biexponential model.
The mathematical model used to describe EHC is multiexponential, modifying the distribution and elimination phase profiles to achieve concordance with the observed data. The function used (represented below) is related to multiexponential pharmacokinetics models, but several lag time functions were added to get a model for EHC peaks. Lag time peaks were added for distribution and elimination phases. Sofware to adjust data as Curve Expert Professional v2.5. Typical model used is:
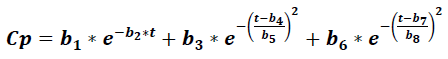
Where Cp is the plasma concentration of a drug at time t, and it accounts for eight parameters (b1 to b8), which relate to the absorption, distribution, and elimination phases for two compartment models, parameters b1 and b2 were related to absorption phase, then lag time functions were considered in this early phase. This model was compared to the classic compartment model:
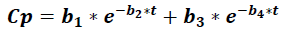
Where Cp is the plasma concentration of a drug at time t, and it accounts for four parameters (b1 to b).
Both models were adapted by calculating their parameters using non lineal regression methodology with the Levenverg-Marquardt algorithm of damped least-squares [31]. The best model was selected through the determination coefficient, error mean squared and the Akaike Information Criterion (AIC) [32], that quantitively evaluated the adaptation of each model. This was also done using SPSS v22. The pharmacokinetic graphs of both formulations were designed with Sigma Plot v11, while the model graphs were designed with software Maple v18.
3. Results
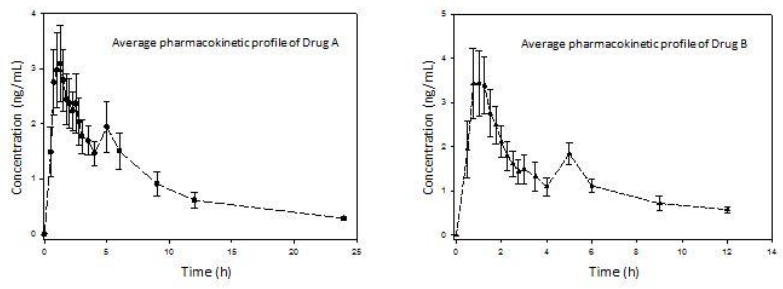
A total of 8 subjects participated in the study, the mean age being 28.62 years old, mean weight of 67.69 kilograms, mean height of 1.63 meters and mean BMI of 25.18 kg/m2. Regarding adverse events, one subject reported frontal headache during the study, with no need of medical intervention or concomitant drug administration. The average pharmacokinetic profiles of both drug formulations were graphed (Figure 1). The main pharmacokinetic parameters were obtained (Table 1). Both drug formulations exhibited a second peak to represent EHC approximately at 5 h. Also, the function parameters for both models (Tables 2 and 3) were calculated.
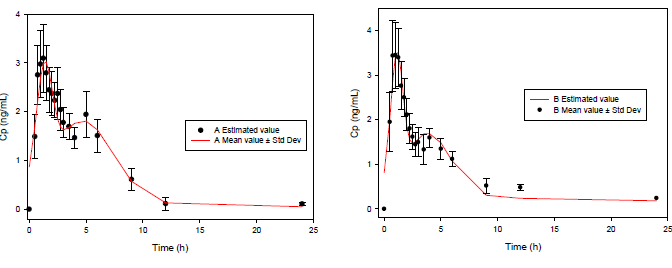
A great difference can be observed between the functions for 4 and 8 parameters. Clearly, the 8-parameter function for ECH displays a good fit (Figure 2), even better than the classical pharmacokinetics model (CME and AIC parameters are lower in all cases).
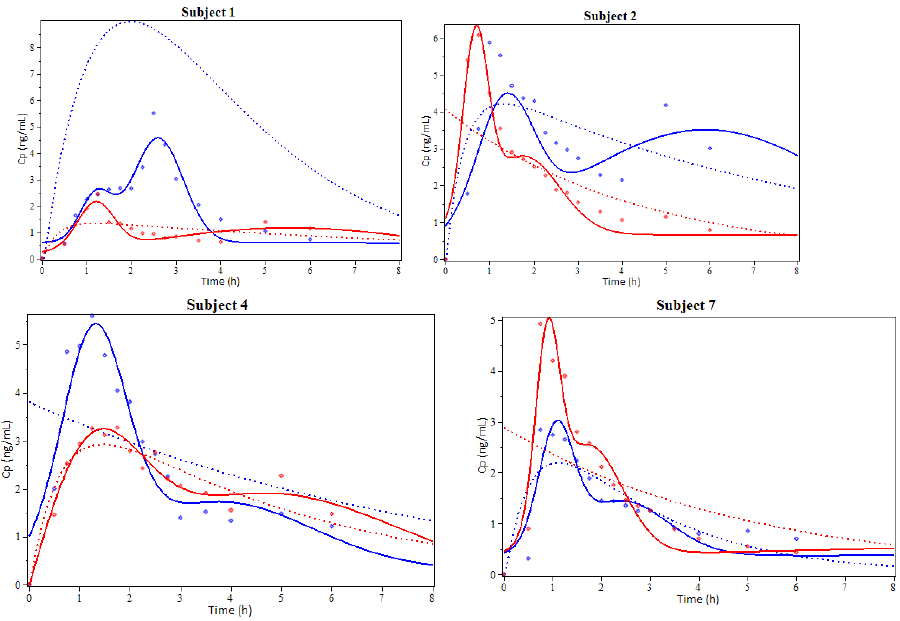
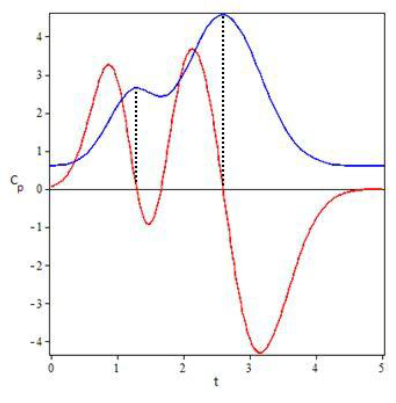
Subjects 1, 2, 4 and 7 were selected to illustrate the model results showing the coinciding degree between plasma concentration profiles for Simvastatin (Figure 3). An additional graph was prepared for the EHC pharmacokinetics function and its derivative to show other model characteristics (Figure 4).
Table 1: Pharmacokinetic parameters for both Simvastatin formulations (20 mg) after a single oral dose for two periods of time in healthy Mexican subjects (n=8). Values represented as mean ± standard deviation
|
Parameter |
Biexponential model |
ECH model |
Trapezoidal method |
||||
|
Drug A |
Drug B |
Drug A |
Drug B |
Drug A |
Drug B |
CVintra |
|
|
AUC0-24h (ng·h/mL) |
12.91 |
12.39 |
20.81 |
18.95 |
22.10 ± 10.56 |
17.16 ± 5.78 |
31.11% |
|
AUC0-∞ (ng·h/mL) |
12.91 |
12.40 |
∞ |
∞ |
26.61 ± 13.10 |
21.09 ± 7.56 |
36.87% |
|
Cmax (ng/mL) |
2.69 |
2.97 |
3.03 |
3.58 |
4.05 ± 1.63 |
4.07 ± 2.18 |
30.48% |
|
tmax (h) |
1.68 |
0.87 |
1.31 |
1.11 |
2.09 ± 1.48 |
1.09 ± 0.35 |
- |
Table 2: Regression parameters of the biexponential pharmacokinetic function
|
Parameter |
Drug A Model 4 parameters Mean value |
Drug B Model 4 Parameters Mean value |
Unit |
|
b1 |
171.342 |
4.401 |
ng/mL |
|
b2 |
0.555 |
0.314 |
h-1 |
|
b3 |
-171.004 |
-4.477 |
ng/mL |
|
b4 |
0.578 |
2.850 |
h-1 |
|
CME |
0.856 |
1.275 |
- |
|
r^2 |
0.568 |
0.440 |
- |
|
AIC |
11.256 |
12.555 |
- |
Table 3: Regression parameters of the EHC pharmacokinetic function
|
Parameter |
Drug A Model 8 parameters Mean value |
Drug B Model 8 Parameters Mean value |
Unit |
|
b1 |
0.15 |
0.31 |
ng/mL |
|
b2 |
0.043 |
0.022 |
h-1 |
|
b3 |
1.696 |
1.405 |
ng/mL |
|
b4 |
4.715 |
3.900 |
h-1 |
|
b5 |
3.784 |
2.802 |
h-1 |
|
b6 |
2.122 |
2.726 |
ng/mL |
|
b7 |
1.319 |
1.111 |
h-1 |
|
b8 |
0.988 |
0.746 |
h-1 |
|
CME |
0.248 |
0.157 |
- |
|
r^2 |
0.884 |
0.922 |
- |
|
AIC |
9.382 |
9.195 |
- |
4. Discussion
The study of drug EHC brings with it a more accurate understanding of the dynamic behavior this process has. The mathematical model used here aims to offer an alternative option for the compartmental models typically used to describe these dynamic mechanisms in EHC. The model can be used as an effective tool to study drugs with this type of behavior, and it also helps explain clinical impact by assessing plasma concentration modifications caused by this phenomenon. This is not easily interpreted by the conventional models.
The evaluation and comparison between performance of both models revealed that the eight-parameter model rendered a better plasma concentration profile adjustment for Simvastatin, since it supplied a lower AIC value and a better r2 (see tables 2 and 3).
Figure 3: Examples of the results from the pharmacokinetic modeling of Simvastatin administered orally. Subjects 1, 2, 4 and 7. The solid line represents the simulation using the EHC pharmacokinetic function, the dotted line represents the simulation using the biexponential function and the dots represent experimental values. Blue is used for Drug A and red for Drug B. (cp: plasmas concentration, h: hours).
It can be observed that the EHC model is closer to the real pharmacokinetic behavior than the biexponential model. This model can also include the delay time (t-lag), useful for EHC modeling.
The classic compartmental models are exponential, and thereby, when the administration is extravascular, the function is biexponential for a one-compartment model and triexponential for a two-compartment model [33]. The classic compartmental function has the following structure:
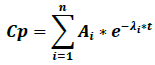
Where Cp is plasma concentration, Ai is the terms of equation coefficients, λi are the first order speed constants for each process, e is the natural logarithm base and t is time. One of the terms of the biexponential function corresponds to the absorption phase and another to the elimination phase.
The EHC model was inspired from the classic compartmental function structure. In this model, the first exponential term corresponds to the absorption phase, and for the function to work, the elimination term of the classic compartmental model was split in two exponentials, one for the early cycle and another for the late one.
The classic compartmental model is modified to include late terms in order to achieve the EHC presence in the CP vs t graphs, which is why the model´s structure changes in the next general model, where the constants αi and βi are related to the early and late cycles of EHC:
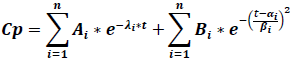
Where Cp is the plasma concentration, Ai are the compartmental function terms ‘coefficients, λi are the first order compartmental function speed constants, Bi are the EHC process coefficients, αi and βi are enterohepatic process constants, e is the natural logarithms‘ base and t is time. As it is shown, the EHC model is a modified compartmental model and it possesses the advantage that it can include the number of necessary peaks to describe a pharmacokinetic profile just by adding the terms of the enterohepatic process.
Figure 3 shows that every Simvastatin concentration peak is somewhat symmetrical and has a bell-like shape. As other studies have suggested, it’s possible that this shape may not be the most adequate to represent every peak [34–37]. This is especially true if we consider that the gallbladder empties during short periods of time and not at all the rest of the time. On this note, the proposed model in this paper is more resembling to the Wajima sinusoidal liberation model [27].
Strictly speaking, the αi and βi values are not exactly equal to the highest width of every peak, since the EHC model is based on the sum of three exponentials, which contribute to the global shape of the curve.
If we only consider two peaks, the following equations can help determine tmax and their respective Cmax:
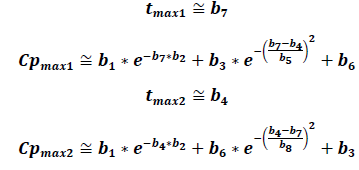
Graphically, it can be proven that these equations provide solid approximations if calculated from the derivative of the EHC model function along with the non-derivative function. The zeros from the derivative function coincide almost perfectly with the tmax of the EHC model function.
Intuitively, the trapezoidal rule method to calculate the AUC will probably overestimate the real value when the drug has EHC. In fact, it has been proven that the AUC depends on sample times in relation to the secondary peaks [14]. In this sense, the models that allow the AUC to be determined using formulas could be helpful to approach the calculations differently. If only two peaks are considered, the next equation would allow the AUC0-t to be calculated:
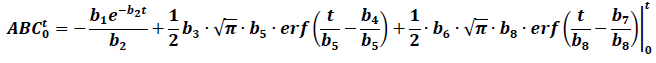
Table 1 shows the calculated AUC using this equation. For the lower or equal values to the last sample time, a similar value to the trapezoidal method is obtained, however, the formula does not provide a finite value for the AUC0-∞, making it less practical in these cases.
5. Conclusions
The application of these models in pharmacokinetic research provides a different vision of the CEH processes, however, in bioequivalence studies it is not a trivial task and it greatly modifies possible acceptance criteria.
In any case, to prove the usefulness of the model, it is necessary to develop further bioequivalence studies to compare the similarity between the AUC using the trapezoidal method in the experimental data and the data obtained from the EHC model.
According to the reported results from previous bioequivalence studies [38], Simvastatin has shown a relatively high intrasubject variability when administered orally, spanning from 20 to 30% for Cmax and AUC variation coefficients, which concur with the data gathered from this pilot study (Table 1). This indicates that a sample size higher than the one stated in Mexican norms is needed to properly execute a bioequivalence study [30].
6. Conflict of Interest:
The authors declare that they have no conflict of interest.
References
- Huntjens DR, Strougo A, Chain A, et al. Population pharmacokinetic modelling of the enterohepatic recirculation of diclofenac and rofecoxib in rats. British Journal of Pharmacology 153 (2008): 1072-1084.
- Ide T, Sasaki T, Maeda K, et al. Quantitative population pharmacokinetic analysis of pravastatin using an enterohepatic circulation model combined with pharmacogenomic Information on SLCO1B1 and ABCC2 polymorphisms. The Journal of Clinical Pharmacology 49 (2009): 1309-1317.
- Adlercreutz H, Martin F, Järvenpää P, et al. Steroid absorption and enterohepatic recycling. Contraception 20 (1979): 201-223.
- Azezli AD, Bayraktaroglu T, Orhan Y. The use of konjac glucomannan to lower serum thyroid hormones in hyperthyroidism. Journal of the American College of Nutrition 26 (2007): 663-668.
- Clements MR, Chalmers TM, Fraser DR. Enterohepatic circulation of vitamin D: a reappraisal of the hypothesis. The Lancet 323 (1984): 1376-1379.
- Steinberg SE, Campbell CL, Hillman RS. Kinetics of the normal folate enterohepatic cycle. The Journal of Clinical Investigation 64 (1979): 83-88.
- Philipps AF, Dvorák B, Kling PJ, et al. Absorption of milk-borne insulin-like growth factor-I into portal blood of suckling rats. Journal of Pediatric Gastroenterology and Nutrition 31 (2000): 128-135.
- Gao Y, Shao J, Jiang Z, et al. Drug enterohepatic circulation and disposition: constituents of systems pharmacokinetics. Drug Discovery Today 19 (2014): 326-340.
- Lehr T, Staab A, Tillmann C, et al. A quantitative enterohepatic circulation model. Clinical Pharmacokinetics 48 (2009): 529-542.
- Tvrdonova M, Dedik L, Mircioiu C, et al. Physiologically motivated time-delay model to account for mechanisms underlying enterohepatic circulation of piroxicam in human beings. Basic & Clinical Pharmacology & Toxicology 104 (2009): 35-42.
- Vree TB, van der ven Andre JA. Clinical consequences of the biphasic elimination kinetics for the diuretic effect of furosemide and its acyl glucuronide in humans. Journal of Pharmacy and Pharmacology 51 (1999): 239-248.
- Miller R. Pharmacokinetics and bioavailability of ranitidine in humans. Journal of Pharmaceutical Sciences 73 (1984): 1376-1379.
- Pedersen PV, Miller R. Pharmacokinetics and bioavailability of cimetidine in humans. Journal of Pharmaceutical Sciences 69 (1980): 394-398.
- Shepard TA, Reuning RH, Aarons LJ. Estimation of area under the curve for drugs subject to enterohepatic cycling. Journal of Pharmacokinetics and Biopharmaceutics 13 (1985): 589-608.
- Shepard TA, Reuning RH, Aarons LJ. Interpretation of area under the curve measurements for drugs subjects to enterohepatic cycling. Journal of Pharmaceutical Sciences 74 (1985): 227-228.
- Roberts MS, Magnusson BM, Burczynski FJ, Weiss M. Enterohepatic circulation: Physiological, pharmacokinetic and clinical implications. Clinical Pharmacokinetics 41 (2002): 751-790.
- Harrison LI, Gibaldi M. Influence of cholestasis on drug elimination: pharmacokinetics. Journal of Pharmaceutical Sciences 65 (1976): 1346-1348.
- Chen HS, Gross JF. Pharmacokinetics of drugs subject to enterohepatic circulation. Journal of Pharmaceutical Sciences 68 (1979): 792-794.
- Steimer JL, Plusquellec Y, Guillaume A, et al. A time-lag model for pharmacokinetics of drugs subject to enterohepatic circulation. Journal of Pharmaceutical Sciences 71 (1982): 297-302.
- Colburn WA, Hirom PC, Parker RJ, et al. A pharmacokinetic model for enterohepatic recirculation in the rat: phenolphthalein, a model drug. Drug Metabolism and Disposition 7 (1979): 100-102.
- Colburn WA. Pharmacokinetic and biopharmaceutic parameters during enterohepatic circulation of drugs. Journal of Pharmaceutical Sciences 71 (1982): 131-133.
- Pedersen PV, Miller R. Pharmacokinetics of doxycycline reabsorption. Journal of Pharmaceutical Sciences 69 (1980): 204-207.
- Funaki T. Enterohepatic circulation model for population pharmacokinetic analysis. Journal of Pharmacy and Pharmacology 51 (1999): 1143-1148.
- Strandgården K, Höglund P, Grönquist L, et al. Absorption and disposition including enterohepatic circulation of (14C) roquinimex after oral administration to healthy volunteers. Biopharmaceutics & Drug Disposition 21 (2000): 53-67.
- Jiao Z, Ding JJ, Shen J, et al. Population pharmacokinetic modelling for enterohepatic circulation of mycophenolic acid in healthy Chinese and the influence of polymorphisms in UGT1A9. British Journal of Clinical Pharmacology 65 (2008): 893-907.
- Jain L, Woo S, Gardner ER, et al. Population pharmacokinetic analysis of sorafenib in patients with solid tumours. British Journal of Clinical Pharmacology 72 (2011): 294-305.
- Wajima T, Yano Y, Oguma T. A pharmacokinetic model for analysis of drug disposition profiles undergoing enterohepatic circulation. Journal of Pharmacy and Pharmacology 54 (2002): 929-934.
- Okour M, Brundage RC. Modeling enterohepatic circulation. Current Pharmacology Reports 3 (2017): 301-313.
- Lennernäs H, Fager G. Pharmacodynamics and pharmacokinetics of the HMG-CoA reductase inhibitors. Clinical Pharmacokinetics 32 (1997): 403-425.
- [30] Secretaria de Salud. NORMA Oficial Mexicana NOM-177-SSA1-2013, Que establece las pruebas y procedimientos para demostrar que un medicamento es intercambiable. Requisitos a que deben sujetarse los Terceros Autorizados que realicen las pruebas de intercambiabilidad. Requisitos [Internet]. México; 2013. Available from: http://www.dof.gob.mx/nota_detalle.php?codigo=5314833&fecha=20/09/2013
- Marquardt DW. An algorithm for least-squares estimation of nonlinear parameters. Journal of the society for Industrial and Applied Mathematics 11 (1963): 431-441.
- Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control 19 (1974): 716-723.
- Wagner JG. Linear pharmacokinetic equations allowing direct calculation of many needed pharmacokinetic parameters from the coefficients and exponents of polyexponential equations which have been fitted to the data. Journal of Pharmacokinetics and Biopharmaceutics 4 (1976): 443-467.
- de Winter BC, van Gelder T, Sombogaard F, et al. Pharmacokinetic role of protein binding of mycophenolic acid and its glucuronide metabolite in renal transplant recipients. Journal of Pharmacokinetics and Pharmacodynamics 36 (2009): 541.
- Rosner GL, Panetta JC, Innocenti F, et al. Pharmacogenetic pathway analysis of irinotecan. Clinical Pharmacology & Therapeutics 84 (2008): 393-402.
- Yau WP, Vathsala A, Lou HX, et al. Mechanism-based enterohepatic circulation model of mycophenolic acid and its glucuronide metabolite: assessment of impact of cyclosporine dose in Asian renal transplant patients. The Journal of Clinical Pharmacology 49 (2009): 684-699.
- Sam WJ, Akhlaghi F, Rosenbaum SE. Population pharmacokinetics of mycophenolic acid and its 2 glucuronidated metabolites in kidney transplant recipients. The Journal of Clinical Pharmacology 49 (2009): 185-195.
- Lee YL, Mak WY, Looi I, et al. Presentation of coefficient of variation for bioequivalence sample-size calculation. International Journal of Clinical Pharmacology and Therapeutics 55 (2017): 633-638.


 Impact Factor: * 3.3
Impact Factor: * 3.3 Acceptance Rate: 74.39%
Acceptance Rate: 74.39%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 