Planning the Yaw Correction Trajectory Based on Current Motor Detection
Weiqiang Ying, Cheng Kuang, Lingyan Zhang, Cheng Yao, Fangtian Ying and Shijian Luo*
Zhejiang University, Hangzhou, 310007, China
*Corresponding Author: Shijian Luo, Zhejiang University, Hangzhou, 310007, China.
Received: 01 October 2022; Accepted: 20 October 2022; Published: 04 November 2022
Article Information
Citation: Ying W, Kuang C, Zhang L, Yao C, Ying F, Luo S. Planning the Yaw Correction Trajectory Based on Current Motor Detection. International Journal of Plant, Animal and Environmental Sciences. 12 (2022): 145-153.
View / Download Pdf Share at FacebookAbstract
This paper describes distributed adaptive methods for solving the trajectory distortion control problem of intelligent lawnmowers. The strategy we have chosen is to use the association of motor current changes with changes in the movement patterns of the trajectory to try to modify the relationship between the fuzzy controller and the Proportional Integral Derivative (PID) controller based on the traditional fuzzy PID control theory to design a new low-cost control scheme. The scheme uses the differences between the current detection and the linearised models as data feedback and interpolates these linear models with the Takagi-Sugeno (T-S) fuzzy method to approximate the entire non- linear model. Then, the concept of parallel distributed compensation (PDC) synthesizes a state feedback controller. A Linear Quadratic Regulator (LQR) is used to stabilize the system and achieve the desired response. A PID fuzzy control method is then used to form the control of the intelligent lawnmower motor. This strategy uses data feedback obtained by monitoring the left and the right motor current fluctuations, and it can be seen from the practical results that the proposed method is effective in obtaining an ideal linear path with good tracking behaviour in various situations. This paper uses the current monitoring change control method to determine whether the bias voltage is tested and confirms that the method can achieve stable path control.
Keywords
<p>PID control, Yaw correction; Trajectory planning</p>
Article Details
1. Introduction
Due to their increasing use in various fields, such as security surveillance, home surveillance for health and entertainment, research and education [1-4], mobile robots have attracted increasing attention, and made advances in the past decade due to their home services and applications.
Since the smart lawnmower can break the problem down into several more manageable parts, these parts can be solved individually, and then combined to solve the overall problem. A complex nonlinear model can be broken down into a set of locally linearised models, and then interpolated to obtain the overall system. This approach is called the Multi-Model-Approach (MMA), also known as T-S modelling [1]. The interpolation of all individual models is carried out using fuzzy logic.
Recently, the use and control of differences between current detection and linearization models as data feedback to enable intelligent lawnmowers to perform certain tasks has attracted a great deal of interest from researchers in related fields. If you compare the results of performing tasks without feed- back with those that do perform tasks with feedback, it becomes clear that the overall performance is more efficient and secure with feedback. The smart lawnmower’s bias is a combination of studying currents and syncing. It has received much attention from autonomous systems and control groups. Cooperative coordination can be described as assigning the left and the right motors to follow a predetermined path of travel while receiving useful information through their sensors and maintaining the prescribed direction. The path trajectory can be coordinates that the intelligent lawnmower must follow or a specified driving area within a certain limit (see [5] and references therein). Dead reckoning has already been extended to a case where a mobile robot moves on uneven terrain. It provides information on positioning for mobile robots by directly calculating parameters, such as position, speed and orientation [6].
In study of Guo et al. [7], the author proposed a mechanism structure for a mobile robot with the advantage of adaptability using hybrid modes with active wheels. There is a large amount of research and literature on smart lawnmowers. Patra et al. [5] from the Indian Institute of Engineering Science, Technology and Technology examined the problem of tracking a smart two-wheel drive lawnmower in detail. By studying the kinematics, dynamics and the linear feedback controller, some basic, e.g., straight and semi-circular trajectories (continuous and discontinuous), were simulated. The real trajectories largely corresponded to the simulation results through experimental results, while the ideal path of the intelligent mower also depended on the actuator [8]. Additionally, various control techniques that were applied to the model were briefly described. Dynamics modelling, simulation and system identification were also examined in other publications. A simple proportional-integral-summation controller was given in Jithu et al. [9] for use. Posture control techniques using an observer were described in Xu et al.
The proprietary sensors measure values within the system (robot), such as battery power, wheel position, joint angle, motor speed, etc. These sensors can be encoders, potentiometers, gyroscopes, compasses, etc. Guo et al. [7] from the Shenzhen Institute of Advanced Technology of the Chinese Academy of Sciences proposed a visual localization system that was important for lawn map creation and area coverage. They used stable light compensation and aimed for the camera mounted on the smart mower towards the ground to extract and match feature points through pairs of frames to locate the smart mower [10]. Guo et al. [7] used MATLAB 2010b software on their computer for data processing, and the program was run on the MATLAB 2010b environment. Experiments proved the feasibility of their positioning system, but the amount of data processed by the computer was large. Some of the main challenges were navigation and path planning, localisation and obstacle avoidance.
The application of fuzzy theory to control systems is widespread in the literature. Mobile robotics has been in development for many years, but for location technology, technology remains a popular research topic for scientists. While there are many different positioning methods and sensors used, there are two broad types of positioning: absolute and relative. Absolute positioning relies on external sensors, etc. to infer the position of the mobile robot directly in the location map, while relative positioning techniques rely on the position in the previous or initial moment to create the final projection [7]. Common absolute positioning techniques include satellite positioning, ultrasonic positioning, Bluetooth positioning, visual positioning, and ultra-broadband UWB positioning. The most important relative positioning technique is dead reckoning. Initially, some authors tried to represent nonlinear systems by piecewise linear approximations [8] using local models and switching. A few years later, Takagi et al. [1]. Navigation is a fundamental problem in robotics and other important technologies. Linear path control or linear control is an important topic in practical application and research. The relative position, posture and speed of an intelligent lawnmower must be controlled to avoid sagging when the travel path changes from the task demands. The most common route method is to use a compass to determine if a distraction is occurring, but compass stability is susceptible to environmental and magnetic influences. Leader-follower control strategies have been widely explored, including various techniques, such as PID control methods [9], and a nonlinear controller has been developed by combining nested saturation with consensus control to achieve a smart lawnmower that can safely track the direction of travel change in a targeted manner.
The mobile robot determines its path in real-time to avoid randomly moving obstacles [10]. Other intelligent algorithms that have been studied by researchers that are used by mobile robots to navigate different environments are the DE (Differential Evolution) algorithm [11,12], HS (Harmony Search) algorithm [13], BA ( Bat Algorithm) [14] and IWO (Invasive Weed Optimization) [15]. To ensure accuracy in the localisation, sensors and an effective positioning system must be considered. Object positioning [16], robotics and AR (Augmented Reality) tracking [17] have been of interest in recent literature. Each of these sensors is used in robots, mobile devices and navigation systems [16,18,19]. The only advantage of using these sensors is to calculate the position and orientation of a device or object. A magnetometer is another sensor that is used to calculate heading angle by sensing the Earth’s magnetic field. They are combined with pose determination technologies [11]. Other methods used for determining indoor localisation include Infrared, Wi-Fi, UWB (Ultra-Wideband), Bluetooth, Wide Local Area NetworkWLAN (), fingerprinting, etc. [20-23]. However, these methods have their shortcomings. Thus, it is necessary to combine two or more schemes to obtain accurate results. It does have the advantage of better performance in terms of accuracy, but it is more expensive and more complex to calculate [24].
In this post, a full dynamic model is used, and the difference between the current detection and the linearization models is used to obtain a linear model. The difference between the obtained linear model and the actual nonlinear system at a certain operating point is added to the linear system, and satisfactory results are obtained by considering disturbances in the design of the controller.
2. Test Platform Construction
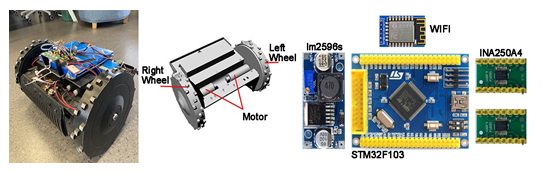
The robot system is conceived by placing it on a mobile platform (Figure 1). The author uses the homemade lawnmower system as a basis to test the theory. The main components include 24 V lithium battery, two DC motors, rack, one STM32F103 main control, two current detection modules (INA250A4), and a Wi-Fi module, through which the experimental platform is built to obtain current data.
2. Methods
The one-way drive wheels going uphill and downhill cause a change in the current and yaw of the mower at the same time, and there is a regular trend. Therefore, there is a theoretical basis for compensating for the motor Hall data based on the current fluctuation. However, it should also be noted that the following derivation (Sections 3, 4, 5) greatly simplifies the actual situation, and the actual situation is much more complex than the theoretical derivation. The main ones include the following:
- The motor power factor differs with different loads and is not a linear number
- Slope surfaces, in addition to the angle, length parameters influence the course and are often accompanied by a wheel slip, which can change the coefficient of friction
- The efficiency of the mower’s power transmission structure varies with different power outputs
- Duty cycle control motors with real-time currents are high-frequency changing data, which makes it difficult to acquire accurate RMS (Rate Monotonic Scheduling) values
For the above reasons, it is difficult to build an accurate mathematical model between the current change and the yaw angle; hence, we use a fuzzy control scheme. Using the current change value and the current change duration as inputs, we create a two-dimensional fuzzy controller, obtain empirical data based on several tests (Figure 2), obtain effective control parameters and finally output suitable Hall compensation data.
3. Theoretical Background of Intelligent Lawn Mower Control
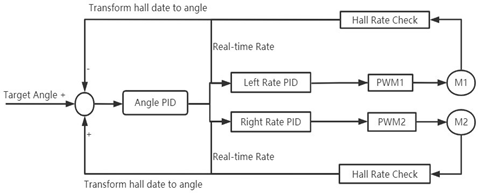
A very important part of the path control of the intelligent mower is to control the car so that it goes straight. It is common practice to set up a serial PID control system for the left and the right wheels, using a heading angle as input and motor Hall data as feedback, with the following control flow diagram (Figure 3).
This solution makes it possible to control the mower to ensure that it drives in a straight line on flat grass. In complex terrain, such as However, for example, on uneven surfaces and slippery surfaces in the rain, the mower will yaw due to the error between the Hall feedback data and the actual distance have the wheels have travelled at that time. In this case, an additional compensation scheme must be added to the basic control scheme.
A common compensation option is to add additional sensors to the mower to aid in course keeping. One of these is the addition of an electronic compass or motion sensor that forms the EMU’s inertial navigation unit. Another option is to add cameras based on machine vision, again with algorithms or mileage and heading data. However, both approaches have certain limitations. One of them is the increasing costs, including the cost of adding and upgrading hardware, and the increasing R and D costs due to the di?iculty of developing software algorithms. The second is the limitations of the use case; the electronic compasses are sensitive to the environment and susceptible to magnetic field interference, motion sensors usually need to be calibrated, and cameras have an unstable image in outdoor sunlight [25,26].
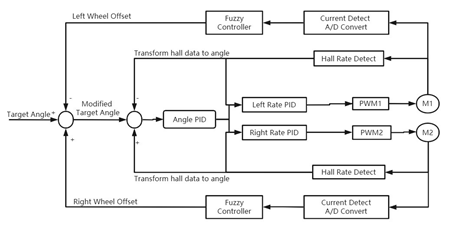
To address this problem, we attempt to devise a new course hold control scheme based on the traditional fuzzy PID control theory by modifying the relationship between the fuzzy controller and the PID controller (Figure 4). First and foremost, a fuzzy controller is added to the abovementioned serial level PID controller loop for the Hall data [27-29]. This fuzzy controller takes the current fluctuation of the mower’s drive wheel motor as input and outputs various Hall compensation data for different amounts of current fluctuation (Figure 4).
4. The effect of grassland terrain on mower deflection
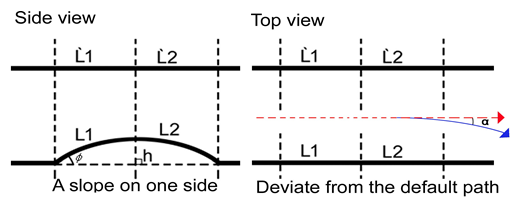
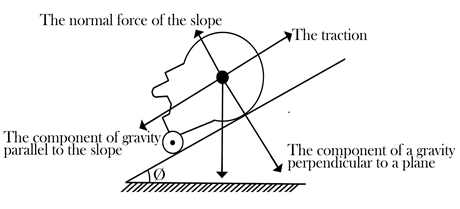
In grassy terrain, two wheels driving over a slope at the same time do not cause yaw. Above all, the difference in gradient between the left and right wheels when driving over the slope causes the mower to deviate from its original direction of travel. This leads us to analyse the situation on an uphill bike.
As seen in the diagram (Figure 5), the distance travelled by the two wheels is different, and the difference determines the yaw angle since it is a single wheel crossing the ramp.
There are the following relationships:
ΔL = L1 · (1 − cosΦ)----(1)
α = ΔL/R---- (2)
The combination of the above two an equation is as follows:
α = L1 · (1 − cosΦ)/R----(3)
The vehicle’s yaw angle is α, the length of ramp L1, θ is the angle between the ramp and the ground, and R is the wheelbase of the two wheels of the vehicle. According to formula (3), the longer the slope length is, the larger the angle between the slope and the ground, and the more likely it is that the car will yaw.
5. The effect of grassy terrain on motor current
As mentioned above, the main influence on yaw in a grassy terrain is the difference in slope between the two wheels. Therefore, here, we analyse the influence of the slope areas on the current of the drive wheel motors (Figure 6).
Since the speed of the trolley motor is controlled by a PID speed loop, the speed can be adjusted in an instant, and thus, it can be viewed as a constant uphill speed. The engine output at this point is equal to gravity. There is the following relationship:
P = U · I · η = F · V = M · ω ----(4)
Ff = m · g · cosΦ----(5)
F = Ff----(6)
The combination of the above 3 equations are as follows:
I = m · g · v · sinΦ/(U · η)---- (7)
where m is the mass of the trolley, v is the linear speed of the trolley wheels, U is the motor drive voltage, I is the motor drive current, η is the motor efficiency and θ is the angle between the slope and the ground. From the above equation, it can be concluded that the larger the slope angle is, the larger the motor current; the longer the slope is, the longer the duration of the high current.
6. Discussion
Before the effectiveness of the fuzzy control could be tested, a tool had to be introduced that could localize the position of the trolley in real-time, and thus, visually monitor the trolley course offset. The wireless location system UWB (accuracy ± 5 cm) was chosen here.
6.1 Experimental site setup
This time, several iterations of the experiment were used to count the effect of the fuzzy control compensation. To ensure consistent conditions for multiple experiments, the experimental site was set up as follows (Figure 7).
The guide groove of the trolley is designed at the starting position to ensure that the trolley starts in the same direction every time, and the road conditions are the same after repeated experiments.
The UWB-3D positioning system is arranged and added to the Trolley UWB tags added, which can provide real-time feedback on the position of the trolley.
6.2 Experimental data pre-processing
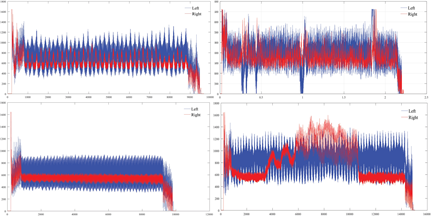
The focus is on processing motor detection currents using PWM controlled motors with high-frequency vibration data for current values, as shown in the following Figure 8.
Ff = m · g · cosΦ---- (8)

Imax is the current maximum, It is the current in real-time, Lt, I(t1) are time window values, and 0.5*W is the error value compensation (Cycle-specific values). The current data after processing with this method are as follows:
The above diagrams (Figure 9) show the motor current values after the maximum value, and the test conditions are wheel idling and real grass driving with different applied resistances. The amplitude of the current data in the graph is already very small and is very clearly reflected in the ramp resistance. Therefore, it can be used as an input for the fuzzy control.
6.3 Experimental Analysis
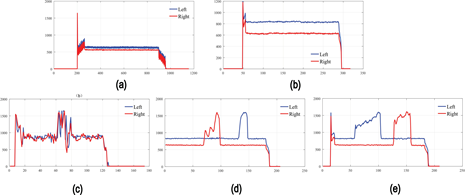
The first set of experiments: (a) Trajectory orientation test without the fuzzy controller. The trolley control algorithm does not include a fuzzy controller. Thus, the trolley starts along the guide slot, goes straight for a distance, passes a small manually designed ramp, and then moves on to reach a position to reach the end. The UWB position data of the entire process are recorded in real-time, that is, the trajectory of the car. The above experiment was repeated 10 times, and the trajectory data were obtained 10 times and plotted as follows. (b) Trajectory orientation test with the addition of a fuzzy controller. The fuzzy controller was added to the trolley control algorithm, and the other conditions were exactly the same as in (a). The experiment was repeated 10 times, and the trajectory data were obtained 10 times. The trajectory data without the fuzzy control and the trajectory data with the fuzzy control essentially lie on a smooth surface.
The second series of tests (Figure 10 (c, d) is the half bump test. To avoid coincidence and to better debug the fuzzy control parameters, the experiment was repeated with a different ramp, and the above experiment was repeated.
6.4 Experimental results
From the above comparison tests, it can be concluded that after adding the fuzzy controller to compensate for the Hall data, a better course correction effect is achieved.
7. Conclusion
In this paper, a one-sided control strategy for uneven road conditions is designed. The novelty of our approach is to establish a physical relationship with the differences between the left and right current sensing and linearization models, and then to use the fuzzy inference engine structure of the incremental adaptive fuzzy PID optimizer, in which controller gains are achieved through LQR optimization to stabilize the system and obtain the desired response. The leader-follower method is then used to provide control for a pair of left and right motors. Different cases are tested to obtain the desired path. Regardless of the different definitions given, sensor fusion is the integration of information from multiple sources to improve the accuracy and quality of the content with the aim of reducing costs. It can be observed that the new linearization method and the proposed fuzzy control give a good tracking response, and the results obtained are actually tested to obtain good results, allowing a new way of thinking for controlling the course stability of the path. The shortcoming of this work is that the realistic conditions prevent the test site from digging a pit, and thus, cannot be tested for concave surfaces. Nevertheless, similar results can theoretically be derived from the test results on raised surfaces, and the plan for our next work has to be considered as a test on concave surfaces.
8. Declarations
Ethics approval and consent to participate
Not applicable.
Conflict of interest
No potential conflict of interest was reported by the authors.
Dataset to be available
All data generated or analysed during this study are included in this published article.
Consent for publication
Not applicable.
Funding
Not applicable.
Authors’ contributions
Weiqiang Ying analyzed and visualized the data and wrote the manuscript. Cheng Kuang analyzed and interpreted the data, Lingyan Zhang collates data and writes the first draft, Cheng Yao analyzed the data and proofread and edited, Fangtian Ying analyzed the data, Shijian Luo proofread and edited. All authors read and approved the final manuscript.
Acknowledge
The authors acknowledge the Computer Aided Product Innovation Design Engineering Centre, Ministry of Education, for providing some of the experimental data and helpful discussion and suggestions.
Authors’ information
Weiqiang Ying, study in electrical and control engineering for the PhD at Zhejiang University in 2019, and he joined the Ministry of Education of Computer Aided Product Innovation Design Engineering Centre. His research interests include sliding mode control, motion control, and signal processing.
Cheng Kuang, Engineer at the Computer Aided Product Innovation Design Engineering Centre, Ministry of Education. Mainly engaged in research in the field of information product design and human-computer interaction Lingyan Zhang, Information Product Design, School of Software, Zhejiang University. Mainly engaged in research in the field of information product design, human-computer interaction, and children’s health and learning.
Cheng Yao, Instructor of Information Product Design, School of Software, Zhejiang University. He is the deputy director of the Computer-Aided Product Innovation Design Engineering Centre of the Ministry of Education and a member of the International Computer Society (ACM). Mainly engaged in research in information product design, technology design, human-computer interaction, industrial design, digital art and design, etc.
Fantian Ying, Professor, Zhejiang University, Deputy Director of Zhejiang Province Service Robot Key Laboratory. Mainly engaged in research in the field of industrial design and integrated product innovation design.
Shijian Luo, Professor, Zhejiang University, Ph. Research interests in industrial design, user experience and product innovation design, service design, ergonomics and human-computer interaction design.
Appendix A:
Relevant data and information
https://github.com/laringying88/Planning-the-yaw-correction-trajectory
References
- Takagi MT, Sugeno: Fuzzy identification of systems and its appli- cation to modeling and control (1985).
- Kumar GA, Hancke Phala KS. Air quality monitoring system based on iso/iec/ieee 21451 standards. IEEE Sensors Journal 16 (2016): 5037-5045.
- Mester G. Motion control of wheeled mobile robots modeling of the wheeled mobile robots (2006).
- Hancke GP, Markantonakis KE, Mayes K. Security challenges for user-oriented rfid applications within the “internet of things”. Journal of Internet Technology 11 (2010): 7.
- Patra S, Nandy B. Lawn mower trajectory tracking by wheeled mobile robot: Its consequences. In: International Conference on Electron- ics (2017): 1-7.
- Jin-Xia YU, Cai ZX, Duan ZH, et al. Design of dead reck- oning system for mobile robot. Journal of Central South University of Technology 13 (2006): 542-547.
- Guo H, Wu X, Fu R, et al. Robust localization system for an autonomous mower. In: IEEE International Conference on Robotics and Biomimetics (2016).
- Endo G, Hirose S. Study on roller-walker (multi-mode steering control and self-contained locomotion). In: Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065) (2002).
- Choi IS, Choi JS. Leader-follower formation control using pid con- troller. In: International Conference on Intelligent Robotics and Applications (2012).
- Aenugu V, Woo PY. Mobile robot path planning with randomly mov- ing obstacles and goal. International Journal of Intelligent Systems and Applications 4 (2012).
- Bird J, Arden D. Indoor navigation with foot-mounted strapdown inertial navigation and magnetic sensors [emerging opportunities for localization and tracking]. Wireless Communications IEEE 18 (2011): 28-35.
- Parhi DR, Kundu S. Navigational control of underwater mobile robot using dynamic differential evolution approach. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment (2016).
- Kundu S, Parhi DR. Navigation of underwater robot based on dynam- ically adaptive harmony search algorithm. Memetic Computing 8 (2016): 125-146.
- Wang GG, Chu HCE, Mirjalili S. Three-dimensional path plan- ning for ucav using an improved bat algorithm. Aerospace Science and Technology 49 (2016): 231-238.
- Sengupta A, Chakraborti T, Konar A, et al. Energy efficient trajectory planning by a robot arm using invasive weed optimization technique. In: Nature and Biologically Inspired Computing (2011).
- Erdem AT, Ercan AO. Fusing inertial sensor data in an extended kalman filter for 3d camera tracking. IEEE Transactions on Image Processing 24 (2015): 538-548.
- Kumar K, Varghese A, Reddy PK, et al. An improved tracking using imu and vision fusion for mobile aug- mented reality applications. International Journal of Multimedia and Its Applications 6 (2014).
- Azuma RT. A survey of augmented reality. Presence: Teleoperators and Virtual Environments 6 (1997): 355-385.
- Benser ET. Trends in inertial sensors and applications. In: 2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS) Proceedings (2015).
- Nasir AK, Hille C, Roth H. Data fusion of stereo vision and gyro- scope for estimation of indoor mobile robot orientation. Ifac Proceedings Volumes 45 (2012): 163-168.
- Sibai FN, Trigui H, Zanini PC. Evaluation of indoor mobile robot localization techniques. In: International Conference on Computer Systems & Industrial Informatics (2012).
- Santosh S, Jae-Young P. Practical fingerprinting localization for indoor positioning system by using beacons. Journal of Sensors 2017 (2017): 1-16.
- Silva BJ, Hancke GP. Practical challenges of ir-uwb based ranging in harsh industrial environments. In: IEEE International Conference on Industrial Informatics (2015): 618-623.
- Yang Y, Meng X, Gao M. Vision system of mobile robot combining binocular and depth cameras. Journal of Sensors 2017 (2017): 1-11.
- Coito F, Eleutério A, Valtchev S. Tracking a mobile robot position using vision and inertial sensor. In: Doctoral Conference on Computing, Electrical and Industrial Systems (2014).
- Hol JD, SchöN TB, Luinge H, et al. Robust real-time tracking by fusing measurements from inertial and vision sensors. Journal of Real-Time Image Processing 2 (2007): 149-160.
- Rong X, Özgüner U. Sliding mode control of a class of underactuated systems. Automatica 44 (2008): 233-241.
- Jithu G, Jayasree PR. Quadrotor modelling and control. In: 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT) (2016).
- Rubio F, Valero F, Llopis-Albert C. A review of mobile robots: Con- cepts, methods, theoretical framework, and applications. International Journal of Advanced Robotic Systems 16 (2019): 172988141983959.





 Impact Factor: * 4.1
Impact Factor: * 4.1 Acceptance Rate: 75.32%
Acceptance Rate: 75.32%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 