Phenomenological and Statistical Study of the First COVID-19 Pandemic
Vassilis Pontikis1*, Theodoros Karakostas2, Philomela Komninou2
1Commissariat à l’Energie Atomique et aux Energies Alternatives, Université Paris-Saclay, Institut Rayonnement-Matière de Saclay (IRAMIS), 91191 Gif-sur-Yvette, Cedex, France
2Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, GR-54124, Greece
*Corresponding author: Vassilis Pontikis, Commissariat à l’Energie Atomique et aux Energies Alternatives, Université Paris-Saclay, Institut Rayonnement-Matière de Saclay (IRAMIS), 91191 Gif-sur-Yvette, Cedex, France
Received: 07 October 2021; Accepted: 15 October 2021; Published: 21 October 2021
Article Information
Citation: Vassilis Pontikis, Theodoros Karakostas, Philomela Komninou. Phenomenological and Statistical Study of the First COVID-19 Pandemic. Archives of Clinical and Biomedical Research 5 (2021): 814-827.
View / Download Pdf Share at FacebookAbstract
Daily rates of infections and deaths collected in several countries during the first SARS-CoV2 (COVID-19) pandemic are approximated by Gaussian functions of the time elapsed since the dates of first occurrence in each country. This representation reveals designating consistently the time evolution of the country-specific daily rates and of the corresponding total duration of the epidemic. Moreover, the appropriate choice of scale units transforms case numbers and time instances to dimensionless quantities and leads to condensing data from twenty-three countries on two master Gaussian curves (infections/deaths). Thereby, data deviations from the average Gaussian behavior are quantified via error bars integrating the effects of local epidemic specificities, of counting errors and of low statistics. The Gaussian master representation helps fixing unambiguously the epidemic peaks and anticipates the duration of the epidemic while discriminating country data that abnormally depart from the average behavior. Finally, this method builds a basis for investigating the evolution of the epidemic in different countries and for establishing comparisons between country-specific public health policies.
Keywords
Epidemic evolution; SARS-CoV2; Phenomenology; Statistics
Article Details
1. Introduction
Statistical analyses combined with mathematical modeling of epidemic data are considered by health organizations as substantial tools for developing prevention policies to limit the propagation of an epidemic while sustaining health systems and contributing to lower human and economic losses [1-5].
The emergence of COVID-19 has motivated several modeling studies for predicting the virus spreading and the basic reproduction factor, R0 with aim to identify how public policies influence the epidemic evolution [6-16]. With this motivation epidemic data from different countries were also statistically analyzed by means of distribution functions capable of localizing in time the epidemic peak via phenomenological extrapolations or machine learning and network analysis techniques [17-22]. Nevertheless, modeling is difficult because data collected by health organizations and other information channels [23-25] are affected by large fluctuations, especially close to the epidemic peak.
Additionally, cardinal numbers of affected population sets and space and time distributions of primary infectious seeds are country-specific, hindering thereby the comparative assessment of the corresponding public health policies [26-28]. However, exploring the data and the social countermeasures intended to limit the virus spreading over the time interval encompassing the first epidemic wave reveals features common to most countries. These features are as follows: (i) the time evolution of the per country cumulated numbers of infections/deaths is sigmoidal in shape, (ii) the corresponding time derivatives look therefore reasonably Gaussian, (iii) the daily number of new infections is underestimated in absence of generalized and systematic tests. Indeed, during the period of the first epidemic wave this study focuses on, recorded daily rates identify principally individuals who claimed medical assistance and their contacts (iv) unlike infections, daily rates of deaths are closer to reality despite possible classification and counting errors whereas in absence of vaccination during the period of time covered by this study these are not influenced by causes other than that intrinsic to the virus spreading and, (v) similar countermeasures were applied such as confinement, lockdown, quarantine and travel restrictions.
The phenomenological model developed in the present work incorporates all these features in contrast with current epidemic modeling. Thereby the otherwise difficult task of comparing the evolution of the epidemic in different countries becomes possible.
In the following, the model and the associated methodological and computational details are first presented. Then we report the results of a model-guided statistical analysis, the conclusions reached thereby and shortly comment on the limitations of the adopted method. Finally main conclusions are listed together with directions for future work.
2. Model, Data, Methods and Computations
2.1 The Gaussian model
The present work relies on the already published phenomenological observation that the numbers of daily new cases, n(t), infections or deaths, evolve as Gaussian functions of the time, t, elapsed since the occurrence of the first case [18] (common features i and ii above):
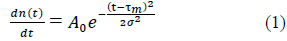
where, τm locates in time the epidemic peak, σ is the standard deviation and A0 corresponds to the maximum of daily cases at t= τm. Integration of eq. (1) over the elapsed time interval [0, τ] yields the total number of cases expected at elapsed time τ:
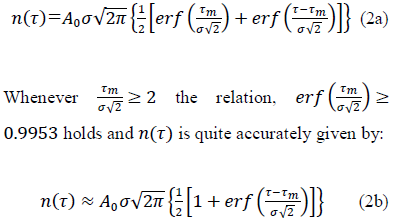
With 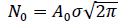 the total number of cases reached upon vanishing of the epidemic at elapsed time, . It is worth noting that the above inequality is always verified, which is further commented on in section 2.3 (Methods and Computations). Eqs. (1, 2a-2b) are referred hereafter to as the Gaussian model.
the total number of cases reached upon vanishing of the epidemic at elapsed time, . It is worth noting that the above inequality is always verified, which is further commented on in section 2.3 (Methods and Computations). Eqs. (1, 2a-2b) are referred hereafter to as the Gaussian model.
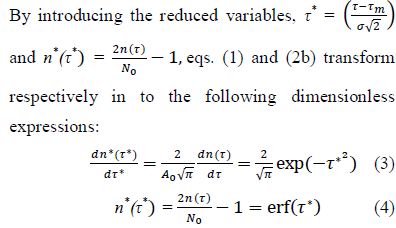
Eqs. (3, 4) are referred hereafter to as the Master representation of the epidemic evolution. Relying on these parameter-free equations, the comparison of the epidemic evolution in countries with different populations, public health systems, epidemic reproduction factors, daily rates of cases and adopted countermeasures, becomes feasible. These aspects are accounted for by the parameters defining the reduced variables,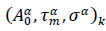 where indices,
where indices, 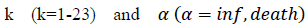 represent respectively the country datasets and their kinds, infections or deaths. Least-squares fits of eq. (4) to the data provides optimal values of the parameters for any considered country (section Methods and Computations).
represent respectively the country datasets and their kinds, infections or deaths. Least-squares fits of eq. (4) to the data provides optimal values of the parameters for any considered country (section Methods and Computations).
Unlike this separate processing of individual datasets yielding country-specific information (epidemic, lower scale), merging the reduced country datasets produces four dimensionless, graphical representations (eqs. (3-4), infections/deaths). These Master representations allow for comparing the epidemic evolution in different countries (pandemic, upper scale), whereas eqs. (3-4) describe the average pandemic behavior. In the context of mobility restrictions, reduced new daily cases, 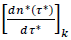 and cumulants of cases,
and cumulants of cases, 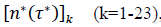 can be viewed as the realizations of independent random variables relating to the same stochastic process operating in any country and lying beneath the epidemic spreading (common feature v). Describing the distribution of infections via the Gaussian model deserves particular attention because the evolutive and differentiated between countries testing policies strongly influence the numbers of observed cases (common feature (iii)). Conversely, the model is applicable to the distribution of death cases with more confidence (common feature iv).
can be viewed as the realizations of independent random variables relating to the same stochastic process operating in any country and lying beneath the epidemic spreading (common feature v). Describing the distribution of infections via the Gaussian model deserves particular attention because the evolutive and differentiated between countries testing policies strongly influence the numbers of observed cases (common feature (iii)). Conversely, the model is applicable to the distribution of death cases with more confidence (common feature iv).
Cardinal numbers of the reduced datasets produced by merging country-specific information increase linearly with the number of considered countries. Thereby, the statistical treatment of data dispersion around the Master representations becomes possible and confidence intervals for the mean can be computed at any reduced time instance, , by assuming that deviations around the mean are normally distributed.
It is worth underlining that merging together reduced data from different countries makes sense whenever the respective epidemic rates are uncorrelated, which sounds reasonable because countries with travel and low mobility restrictions holding assimilate to closed and non-interacting systems (common feature v).
2.2 Data
Raw data in the form of time series of cumulated numbers of infections/deaths, updated on a daily basis, have been collected from official sources for 23 selected countries experiencing the endemic since January 22, 2020 [23-25].
These time series of cumulated events display fluctuations of uncertain origin, in violation of the expected monotonic increase of total cases as functions of elapsed time. Although smoothing through sliding averages over a few days interval greatly reduces such fluctuations, raw unbiased data have been used throughout this study.
Epidemic data for Australia and China from Ref. 23 are split in several regional files. These were merged here in to a single file with the numbers of infections and deaths obtained as cumulants of the corresponding regional data.
It should be noted that before the chosen starting date, no epidemic events were announced in the countries entering the present study but China, which epidemic starting date is still ambiguously known. For each country data were considered over a time period ΔT long enough to ensure that the first epidemic peak has been crossed unambiguously. This condition fixes the parameters of the homothetic transformations yielding the Master representations (section 2.1).
This information is displayed in Table 1, whereas the columns labeled and  list per country the number of days elapsed since the time origin (January 22, 2020) till the occurrence of the first cases, infections and deaths respectively.
list per country the number of days elapsed since the time origin (January 22, 2020) till the occurrence of the first cases, infections and deaths respectively.
Table 1: Model and data related parameters per country are identified via the ISO 3166-2, alpha-2 country codes. In column are reported the intervals of time elapsed since January 22, 2020 covered by this study, chosen to include within this time period the first epidemic peak in each country; 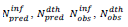 are predicted resp. observed [23-25] cumulated numbers of infections/deaths at τendupon vanishing of the first wave (see text) whereas values between parentheses represent signed relative deviations between predicted and observed values;
are predicted resp. observed [23-25] cumulated numbers of infections/deaths at τendupon vanishing of the first wave (see text) whereas values between parentheses represent signed relative deviations between predicted and observed values;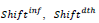 , designate time intervals separating the chosen time origin (January 22, 2020) from dates of first infection resp. death cases and,
, designate time intervals separating the chosen time origin (January 22, 2020) from dates of first infection resp. death cases and, 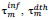 ;are predicted time instances of maximal daily rates. Time distributions of daily rates of infections and deaths hold common the standard deviation, σ (see text) and thus the conventional duration of the first wave, (rounded to the nearest integer).
;are predicted time instances of maximal daily rates. Time distributions of daily rates of infections and deaths hold common the standard deviation, σ (see text) and thus the conventional duration of the first wave, (rounded to the nearest integer).
2.3 Methods and computations
First derivatives of cumulated numbers of events were determined numerically via the central difference scheme working at order O(h3). The sets of parameters, 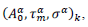 have been numerically calculated for each country, k (k=1-23,&alpha = inf, death) by a least-squares fit of eq. (4) on the numbers of cases. Within any country k common values were assigned to
have been numerically calculated for each country, k (k=1-23,&alpha = inf, death) by a least-squares fit of eq. (4) on the numbers of cases. Within any country k common values were assigned to 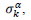 , a decision based on the empirical observation that separate fits yield almost similar values
, a decision based on the empirical observation that separate fits yield almost similar values 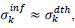 , that reduces the free parameters of the model to five per country. The minimization scheme consisted in defining the following objective function, which closest to zero value corresponds to the optimal model parameters:
, that reduces the free parameters of the model to five per country. The minimization scheme consisted in defining the following objective function, which closest to zero value corresponds to the optimal model parameters:
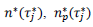
where, the index, j runs over the events of a given country dataset, wj are dimensionless weights with values, wj =10 if |τ∗ j|>1 and wj =1 otherwise, 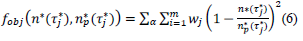 are respectively the observed and predicted numbers of events expressed in reduced units (Eq. (4), section 2.1). The minimization procedure relied on a home-made program interfacing MERLIN [29], a public domain multi-dimensional minimization package. Upon convergence, the procedure yields optimal values of the model parameters for each country (Table 1). With the values of and
are respectively the observed and predicted numbers of events expressed in reduced units (Eq. (4), section 2.1). The minimization procedure relied on a home-made program interfacing MERLIN [29], a public domain multi-dimensional minimization package. Upon convergence, the procedure yields optimal values of the model parameters for each country (Table 1). With the values of and 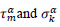 displayed in this table, the condition of validity of eq. (4),
displayed in this table, the condition of validity of eq. (4), 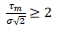 is systematically verified.
is systematically verified.
The Master representations permit a statistical approach of the pandemic to be made, which is not feasible by only considering individually country-specific data. Indeed, contributing countries generate per day equal in number reduced data, which deviations from the daily average behavior (eqs. 3-4) can be treated statistically. This can be accepted by assuming that the endemic evolves in different countries similarly whenever restrictions hold. In this context, the dispersion of the reduced data expresses local specificities including counting errors. The accuracy of the statistical analysis can be further increased via a coarse graining of the reduced time transforming daily data in to a histogram as follows: (1) the reduced time interval over which significant numbers of cases are observed is divided in i=50 contiguous bins of equal length, dτ*≈0.12 for deaths and, dτ*≈0.18 for infections, each containing respectively 42 and 53 elements, (2) to the time instances of the bin centers, 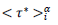 are attributed daily rates,
are attributed daily rates, 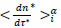 and cumulated numbers,
and cumulated numbers, 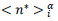 obtained as averages of the data contained in each bin, (3) confidence intervals for the mean are computed from data in the bins at a 99% confidence level with the usual assumption that errors are normally distributed and that Student’s
obtained as averages of the data contained in each bin, (3) confidence intervals for the mean are computed from data in the bins at a 99% confidence level with the usual assumption that errors are normally distributed and that Student’s
t-distribution accounts for the small size of the daily datasets [30-31].
Finally, the phenomenological model yields a conventional estimate of the mean duration of the pandemic, 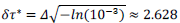 defined as the difference between final and starting time instances when reduced daily rates amount 1‰ of the peak value. Country-specific values are given by,
defined as the difference between final and starting time instances when reduced daily rates amount 1‰ of the peak value. Country-specific values are given by, 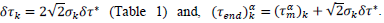
3. Results
3.1 Model validation and country specificities
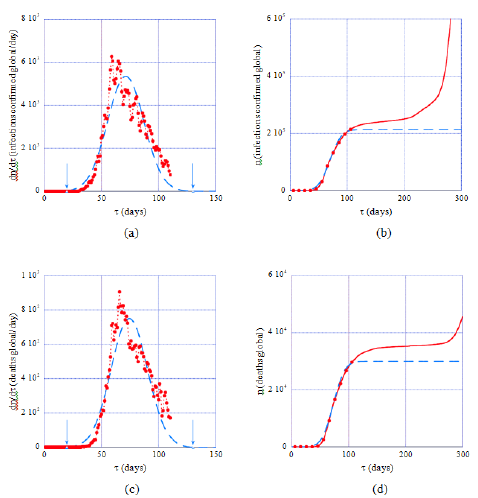
Application of the model to datasets from Italy, taken as a working example of a country that has passed the epidemic peak 110 days after January 20, 2020 shows that predicted daily rates and cumulated numbers of infections fit the data satisfactorily within this time interval (Figure 1, dashed lines). Well after the peak the prediction increasingly underestimates the observed data, which is expected because of the emergence of COVID-19 variants, the generalization of testing and the weakening of mobility restrictions. Similar results are obtained with this modeling of the epidemic for all the countries considered in this work, suggesting thereby that Gaussian and error function forms designate consistently its evolution. The arrows in Figures 1a and 1c mark time instances with daily rates at 1‰ of the maxima of the theoretical graph (full line) and define conventional start and end dates of the first epidemic wave and its effective duration, δt. In Italy δt =118 days whereas values for other countries are reported in Table 1 (last column). These figures show also that on approaching the epidemic peak daily rates are increasingly scattered around the theoretical Gaussian graph, a finding common to all the datasets forming the country database used in the present work. The origin of the observed fluctuations and of their amplification near the epidemic peak are not clear though it is reasonable to admit that counting errors are superimposed to other causes, possibly intrinsic to the epidemic. Conversely, cumulated numbers of cases (Figures 1b, 1d) are less affected by fluctuations, which justifies choosing equations (2b) or (4) for determining optimal, country-specific model parameters.
Table 1 is divided in two parts on the basis of country-specific standard deviation values, s defining two groups with averages, <σ>=14±0.6 and <σ>=40.9±5.2, where uncertainties represent standard errors. In direct relation with s, the first wave of the epidemic in countries of the second group lasted on average three times longer than in these of the first group. This has motivated collecting data over about 110 days for countries in the first group and a ≈2-3 time’s longer interval for these belonging to the second group (column DT in this table). Reasons behind this finding are unclear in absence of an investigation of possible trends existing in the matters of social countermeasures and systems of public health that may differentiate the two groups of countries.
Figure 1: Model predictions (dashed lines) of daily rates of cases (a, c) and of cumulated global numbers (full lines, b, d) in Italy during the first epidemic wave. Full dots and lines represent data collected within the time interval covered by the present study (Table 1, 2nd column). The data scatter in (a, c) shows that locating the epidemic peak is difficult, whereas the model predicts its occurrence at about 71 days (resp. 75 days for deaths) after the chosen time origin (January 22, 2020). Conversely cumulated global numbers of infections are less affected by fluctuations (b, d). Arrows in (a) and (c) mark conventional start/end dates of the epidemic (see text, section 3.2).
3.2 Master representations
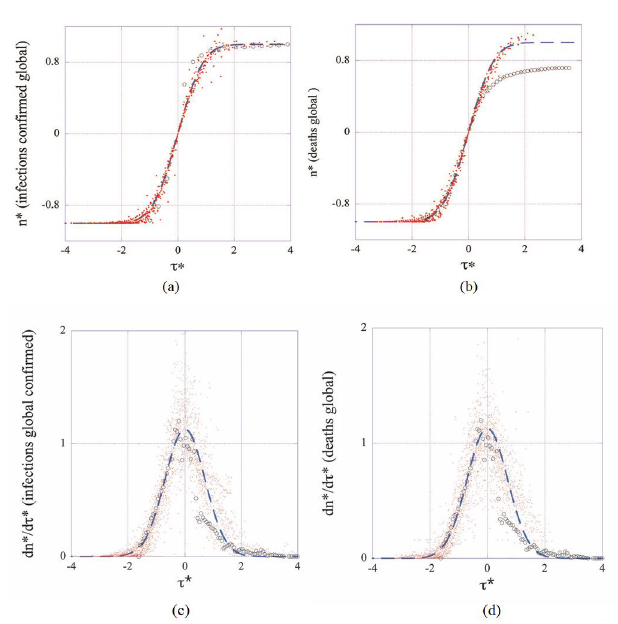
Having determined the parameters of the model 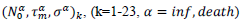 raw datasets have been converted in reduced coordinates and are displayed in Figures 2 (a-d) together with the theoretical predictions (Master representations, eqs. (3, 4)). It can be seen that reduced country-datasets of cumulated cases condense on the displayed graphs with little dispersion, confirming thereby the existence of the above foreseen intrinsic to the epidemic average behavior (Figures 2a, 2b). This suggests that strong similarities underly the evolution of the epidemic in different countries under the contextual conditions listed in the introduction (features iii and v).
raw datasets have been converted in reduced coordinates and are displayed in Figures 2 (a-d) together with the theoretical predictions (Master representations, eqs. (3, 4)). It can be seen that reduced country-datasets of cumulated cases condense on the displayed graphs with little dispersion, confirming thereby the existence of the above foreseen intrinsic to the epidemic average behavior (Figures 2a, 2b). This suggests that strong similarities underly the evolution of the epidemic in different countries under the contextual conditions listed in the introduction (features iii and v).
Figure 2: Master representations of cumulated numbers of infections (a), deaths (b) and of the corresponding reduced daily rates (c, d). For the sake of readability only one every five datapoints are displayed in (a) and (b) whereas all datapoints (N=3210) are present in (c) and (d). Dashed lines represent the master curves (eqs. 3, 4). Datasets from China (open circles) deviate significantly from the average behavior (master curves dashed lines).
Unexpectedly the figures put in evidence that data from China deviate markedly from the average epidemic behavior as is defined by the remaining 22 countries. This is particularly visible in Figures 2 (b-d). The origin of this finding is not yet clear and deserves further investigation well beyond the scope of the present work. Pragmatism has led to discard datasets for China from the statistical analysis. However, this singular case illustrates the discriminating power of the present phenomenological analysis, which constitutes a main, significant result of this work: master representations enable for detecting countries
where the virus spreading differs from the observed average behavior. This also constitutes a starting point for a comparative assessment of public health policies in different countries to be made. Finally, the master representations of daily rates show that transforming real in to dimensionless data does not damp fluctuations (Figures 2 c-d), which motivates for studying this noise statistically as is done below.
3.2). Dashed lines correspond to the master representations (eqs.1, 2) and far outside the error bars characteristic of the average epidemic behavior to data from China (open circles in (d)). Aiming to minimize interference with the second pandemic wave data of the present analysis correspond to t*<3.
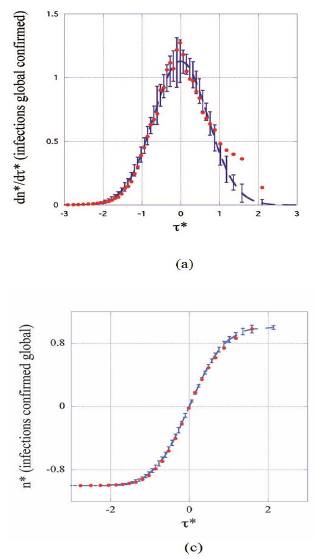
Figure 3: Master plots with error bars: daily rates (a, b) and cumulated numbers (c, d) of infections and deaths as functions of the elapsed time (reduced units). Full dots represent coarse-grained data from all the countries considered in this work (see text, section 3.2). Dashed lines correspond to the master representations (eqs.1, 2) and far outside the error bars characteristic of the average epidemic behavior to data from China (open circles in (d)). Aiming to minimize interference with the second pandemic wave data of the present analysis correspond to t*<3.
3.3 Noise appraisal
Figures 3 (a-d) display the theoretical master curves (dashed lines, eqs. 3-4) drawn together with coarse-grained values (§2.3) of daily rates and of cumulated numbers of cases (full circles) plotted as a function of the reduced time 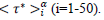 . It can be seen that these fit pretty well the master graphs and that the error bars reproduce faithfully the data scatter for τ*<0.8. Real time widths of the bins used for the coarse graining transformation amount, Δτ≈2-3 days, a period being large enough for drastically damping fluctuations. Since this delay is much shorter than any characteristic time of the epidemic (Table 1) the hypothesis is favored that counting modes of cases are principally responsible of the observed data scatter. However, the theoretical predictions appear systematically underestimating daily rates above τ*>0.8 (Figures 3 a-b, full lines). This trend may originate from both the following reasons namely that the Gaussian description of daily rates is not fully adapted to the evolution of the pandemic and that emerging COVID-19 variants interfere with the first epidemic wave, which is not accounted for by the phenomenological model.
. It can be seen that these fit pretty well the master graphs and that the error bars reproduce faithfully the data scatter for τ*<0.8. Real time widths of the bins used for the coarse graining transformation amount, Δτ≈2-3 days, a period being large enough for drastically damping fluctuations. Since this delay is much shorter than any characteristic time of the epidemic (Table 1) the hypothesis is favored that counting modes of cases are principally responsible of the observed data scatter. However, the theoretical predictions appear systematically underestimating daily rates above τ*>0.8 (Figures 3 a-b, full lines). This trend may originate from both the following reasons namely that the Gaussian description of daily rates is not fully adapted to the evolution of the pandemic and that emerging COVID-19 variants interfere with the first epidemic wave, which is not accounted for by the phenomenological model.
4. Discussion and Conclusive remarks
The present work relies on statistical datasets from twenty-three countries [23-25] and postulates that in all of them the number of daily new cases can be approximated by a Gaussian function of the elapsed time. This modeling is shown to faithfully estimating the time evolution of daily cases during the first manifestation of the epidemic (1st wave). Adopted country-mobility restrictions guarantee that countries are isolated and thus the model can be strictly applied over the corresponding duration. Moreover, observations are not affected in this case by causes external to the endemic such as massive testing and vaccination, which defines a strict context for the present discussion.
Approximating daily cases via Gaussian functions is a central to the present work phenomenological assumption whereas any other bell-shaped functional form could have been employed as well. However, the shape, symmetry and sigmoidal forms of the time integrals of Gaussians are useful properties that have motivated their use for representing the dynamic evolution of the epidemic. These help in localizing the epidemic peak, despite the considerable fluctuations affecting daily data and yield the relaxation time intrinsic to the epidemic (standard deviation of the Gaussians).
The choice has been made in the present work to take identical the standard deviations of the Gaussians modeling daily cases of infections and deaths. Besides reducing the number of independent model parameters, this helps in circumventing uncertainties of infection counts tightly depending on country-specific testing policies. Indeed, these last do not influence the numbers of death cases and the corresponding standard deviation. Thereby, the aforementioned uncertainties are explicitly transferred in the daily rate amplitudes of infections cases, 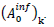 . The predicted numbers of cases,
. The predicted numbers of cases, 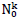 underestimate almost systematically the values
underestimate almost systematically the values 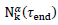 observed at the conventional end of the epidemic.
observed at the conventional end of the epidemic.
The imperfection of the Gaussian model, emerging COVID-19 variants and the evolution in time of the countermeasures are among possible causes of this behavior. It is generally accepted that phenomenology serves in classifying and testing data for internal consistency rather than constituting a predictive tool. However, since country parameters become stationary once the epidemic peak is crossed the conventional dates can be defined,  and the associated duration of the epidemic δτk as well, thus granting the present model with a valuable, predicting power. Finally, error bars from the Master representations (Figure 3) can be converted for any given country in real units thereby offering estimation of the expected maximum daily rates and of cumulated numbers of cases at any time beyond the epidemic peak.
and the associated duration of the epidemic δτk as well, thus granting the present model with a valuable, predicting power. Finally, error bars from the Master representations (Figure 3) can be converted for any given country in real units thereby offering estimation of the expected maximum daily rates and of cumulated numbers of cases at any time beyond the epidemic peak.
The capability of the developed methodology to differentiate countries departing from the average behavior described by the Master representations is a significant result of the present work. However, the explanation of such singularities is not possible without additional investigations.
Acknowledgements
Lina Prakoura, Renée Quillivic and Ioannis Emmanouil are gracefully acknowledged for stimulating discussions, constant support and encouragements.
Competing Interests
The authors have no competing interests or other interests that might be perceived to influence the results and/or the discussion reported in this paper.
References
- OECD report, COVID-19: Protecting people and societies. https://www.oecd.org/inclusive growth/resources/COVID-19-Protecting-people-and-societies.pdf
- Eibensteiner F, Ritschl V, Stamm T, Cetin A, Schmitt CP, et al. Countermeasures against COVID-19: how to navigate medical practice through a nascent, evolving evidence base-a European multicentre mixed methods study. BMJ Open 11 (2021): e043015.
- Zhou Y, Li J, Chen Z, Luo Q, Wu X, et al. The global COVID-19 pandemic at a crossroads: relevant countermeasures and ways ahead, J. of Thoracic Disease 12 (2020).
- Principles of Epidemiology in Public Health Practice: An Introduction to Applied Epidemiology and Biostatistics, third edition, U.S. Department of Health and Human Services, Centers for Disease Control and Prevention (CDC) Office of Workforce and Career Development, Atlanta, GA 30333, October 2006, ( 2012).
- Lemey Ph, Ruktanonchai N, Hong SL, Colizza V, Poletto C, et al. Untangling introductions and persistence in COVID-19 resurgence in Europe, Nature 595 (2021): 713.
- Siettos CI, Russo Mathematical modelling of infectious disease dynamics. Virulence 4 (2013): 295-306.
- Adam Modelling the pandemic. Nature 580 (2020) : 316-318.
- Heesterbeek H, et Modeling infectious disease dynamics in the complex landscape of global health. Science 347 (2015): 6227.
- Cobey Modeling infectious disease dynamics. Science (2020): eabb5659.
- Anastassopoulou C, Russo L, Tsakris A, Siettos Data-based analysis, modelling and forecasting of the covid-19 outbreak. PLoS ONE 15 (2020): e0230405.
- Zhu Y, Chen Y On a statistical transmission model in analysis of the early phase of covid-19 outbreak. Stat Biosci (2020).
- Shaikh AS, Shaikh IN, Nisar A mathematical model of covid-19 using fractional derivative: Outbreak in India with dynamics of transmission and control. Preprints (2020).
- Lee MJ, Lee Understanding the temporal pattern of spreading in heterogeneous networks: Theory of the mean infection time. Phys. Rev. E 99 (2019): 032309-1-9.
- Fang Y, et Transmission dynamics of the covid-19 outbreak and effectiveness of government interventions: A data-driven analysis. J. Med. Virol 92 (2019): 645-659.
- Giordano G, Blanchini F, Bruno R, ColaneriP, Di Filippo A, et al. Modelling the covid-19 epidemic and implementation of population-wide interventions in Nat. Med 580 (2020): 317-318.
- Russo Tracing day-zero and forecasting the fade out of the covid-19 outbreak in Lombardy, Italy: A compartmental modelling and numerical optimization approach. medRxiv preprint (2020).
- Khrapov PV, Loginova Comparative analysis of the mathematical models of the dynamics of the coronavirus covid-19 epidemic development in the different countries. Int. j. open inf. technol 8, 5 (2020): 17-22.
- Ciufolini I, Paolozzi Mathematical prediction of the time evolution of the covid-19 pandemic in Italy by a Gauss error function and Monte Carlo simulations. Eur. Phys. J. Plus 135 (2020): 1-8.
- Zou Y, Pan S, Zhao P, Han L, Wang X, et al. Outbreak analysis with a logistic growth model shows COVID-19 suppression dynamics in China. PLoS ONE 15 (2020): e0235247.
- So MKP, Chu AMY, Tiwari A, Chan JNL. Source code for: On topological properties of covid-19: predicting and assessing pandemic risk with network statistics (version v1.0), zenodo (2021).
- Ardabili SF, et Outbreak prediction with machine learning. Preprint (2020).
- Nemati M, Ansary J, Nemati Covid-19 machine learning based survival analysis and discharge time likelihood prediction using clinical data. Preprint (2020).
- Global-projections (2020).
https://covid19-projections.com/#global-projections, https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv, https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv
[Online; last accessed July 2, 2021]. - Today’s data: geographic-distribution-covid-19-cases-worldwide (2021). https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide
- Covid deaths (2020).https://ourworldindata.org/covidcases and https://ourworldindata.org/covid-deaths
- Barmparis GD, Tsironis G Estimating the infection of covid-19 in eight countries with a data-driven approach, Chaos, Solitons Fractals 138 (2020): 109842.
- Attanayake AMCH, Perera SSN, Jayasingh S. Phenomenological Modelling of COVID-19 Epidemics in Sri Lanka, Italy, the United States and Hebei Province of China, Computational and Mathematical Methods in Medicine Volume (2020).
- Sergio A Hojman, Felipe A Asenjo. Phenomenological dynamics of COVID-19 pandemic: Meta-analysis for adjustment parameters, Chaos 30 (2020): 103120.
- Papageorgiou DG, Demetropoulos IN, Lagaris Merlin-3.1.1. A new version of the merlin optimization environment. Comput. Phys. Commun 159 (2004): 70-71.
- Kreyszig Statistische Methoden und ihre Anwendungen (Vandenhoeck and Ruprecht, Göttingen (1973).
- Bonamente, Statistics and Analysis of Scientific Data (Springer, Graduate Texts in Physics (2013).


 Impact Factor: * 5.8
Impact Factor: * 5.8 Acceptance Rate: 71.20%
Acceptance Rate: 71.20%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 