Logarithmic Quadratic Regression Model for Early Periods of COVID-19 Epidemic Count Data
Daisuke Tominaga*
Cellular and Molecular Biotechnology Research Institute, National Institute of Advanced Industrial Science and Technology, Ibaraki, Japan
*Corresponding author: Daisuke Tominaga, Cellular and Molecular Biotechnology Research Institute, National Institute of Advanced Industrial Science and Technology, AIST Tsukuba Central 5, 1-1-1 Higashi, Tsukuba, Ibaraki 305-8565, Japan
Received: 18 August 2021; Accepted: 25 August 2021; Published: 24 September 2021
Article Information
Citation: Daisuke Tominaga. Logarithmic Quadratic Regression Model for Early Periods of COVID-19 Epidemic Count Data. Archives of Clinical and Biomedical Research 5 (2021): 763-793.
View / Download Pdf Share at FacebookAbstract
Background: While COVID-19 epidemic has been spreading worldwide, its characteristics are still unclear. The development of good mathematical models for predicting its prevalence and subsiding is strongly expected. The epidemic curve shows how the epidemic increases and subsides. This is the number of persons found infected daily. To express this with a mathematical model, the compartment model such as the SIR model is used generally. However, model parameter values of these ordinary differential equation based models are very sensitive for errors of observed data, and it is often difficult to find a reliable model especially when the amount of data is not sufficient. On the other hand, a regression model with a small number of parameters is more robust against data errors than a highly sensitive nonlinear differential equation model, though, it is not clear what a good regression model is for epidemic data.
Methods: We modeled the initial emerging period of the epidemic curve of COVID-19 in Tokyo with a model that introduces a quadratic polynomial function to the logarithms of the numbers of infected cases, and modeled it with other regression models including the generalized linear model to compare.
Results: It was shown that the statistical properties of the logarithmic quadratic function model were good even in the early stages of the epidemic, which is generally said to increase exponentially and monotonically. By applying the logarithmic quadratic function model to the data of the number of cases in each country of the world, the starting and the subsiding dates of the epidemic and the total number of cases in each country were estimated.
Conclusions: Although an epidemic curve in an early period said generally to be exponential, namely linear in the logarithmic space, a quadratic curve regression fits better than the linear and the generalized linear model. These es
Keywords
<p>Regression analysis, Logarithmic count data, Quadratic exponential function, Bell curve, Linear regression, Generalized linear model</p>
Article Details
1. Introduction
While COVID-19 epidemic has been spreading worldwide, its characteristics are still unclear. The development of good mathematical models for predicting prevalence and subsiding is strongly expected. The epidemic curve shows how the scale of the infection increases. For example, this is a time series of the number of infected persons confirmed in a day, or daily epidemic count data. When this is expressed by a mathematical model, compartmental models such as the SIR model [1-3], and regression with an exponential function [4] are used generally. The number of infected persons per day is the difference in the cumulative number of infected persons, and ordinary differential equations (ODEs) or difference equations are often used in these models. The exponential regression model is used when the difference and accumulation are increasing rapidly in the early period of epidemic. The exponential regression is equivalent mathematically to the linear regression of logarithms of count data.
In the compartment model with simultaneous differential equation systems, the values of parameters such as basic production number R0, incubation period, and period with infectious ability must be determined [1, 2]. However, it is rare that they can be determined by experimental observation for new infectious diseases, especially in the early period of the epidemic, so they are determined by searching for parameter values that best fit the model to the time series of the epidemic counts. Parameter estimation uses a nonlinear numerical optimization method in general, but the optimum parameter values fluctuate greatly due to slight errors in the observed data. It is often difficult to obtain a reliable model when the amount and accuracy of data are not sufficient [4, 5]. Models with a small number of parameters may be more robust to data errors than nonlinear and sensitive ODE models. Regression of the epidemic count data by the exponential function and regression of the logarithm of the epidemic count by a linear or a quadratic function can be easy at model parameter estimation. These regressions may robust for data with large errors or small sample sizes.
Since the epidemic count is a non-negative integer, and it seems to increase exponentially in the early period of the epidemic, the generalized linear model (GLM) that uses the logarithmic transformation for the link function and Poisson distribution for the error distribution can be expected as a good model [6]. In this model, it is expected that the logarithms of the epidemic counts will be linear with time, but it has not been proven. GLM, and the exponential function, are monotonically increasing, though the epidemic count increases and then decreases generally [4]. A time series of the epidemic count, or an epidemic curve is often depicted as a bell shape curve [5]. A typical mathematical model of a bell curve is the exponential quadratic function, that is used for the probability density function of the normal distribution. This is represented as a simple quadratic polynomial function by logarithmic transformation, and has two zeros. These two zero points can be considered the epidemic's starting and subsiding points, and this starting point can be an approximate value of the transition point from the endemic to the epidemic. Also, if the epidemic curve is divided into two periods, namely steady fluctuation and bell shape curve periods, each may correspond to an endemic and an epidemic. We applied a model that introduces a quadratic polynomial function to the logarithms of the epidemic count data, that is, the logarithmic quadratic function model, to model the transition of the epidemic counts in the early period of the epidemic of COVID-19 in Tokyo. The accuracy and statistical properties were compared with other regression models, the exponential regression and GLM. We searched for the data range where the model fits best for each model.
As a result, it is shown that the logarithmic quadratic function model has better statistical properties even in the early period of the epidemic, which is said to increase exponentially and monotonically. We estimated the starting and the subsiding dates of the epidemic and the total number of cases in each country by applying the logarithmic quadratic function model to the epidemic count data in 114 countries in the world. These estimates can be informative to reveal the transition mechanism from endemic to epidemic, and epidemic to pandemic.
2. Method
2.1 Data
We used two datasets on the number of persons found infected per day, Tokyo and International datasets. These are published by Tokyo metropolitan government and European Centre for Diseases prevention and Control (ECDC). Modeling was performed by removing days with a count of 0 in the Tokyo data and days with a count of 2 or less from the international data.
2.2 Formulae
2.2.1 Logarithmic quadratic model: The logarithmic quadratic function is fitted to logarithm of epidemic count data y(x) as follows;
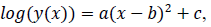
where x is a number of days from the beginning of the data, y(x) is a number of persons found infected in the day x, a, b and c are model parameters. x and y are natural numbers and a, b and c are real numbers. Two zero points of the logarithmic quadratic function that fit to the daily epidemic count data are represented by model parameters a, b and c as follows:
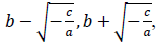
where -c/a is positive when the fitted function is convex upward, or a < 0 and c > 0, and logarithm of a typical epidemic curves are convex upward. Therefore, the estimated epidemic period is represented as 2{(-c/a)^0.5}, and the estimated maximum daily epidemic count is exp(c). When log(y(x)) is represented by a quadratic polynomial function as shown above, y(x) is represented by an exponential quadratic function as follows:
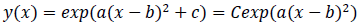
where C is exp(c). Here let the N(x) is the probability density function of the standard normal distribution of which the mean is 0 and the variance is 1. N(x) is defined as follows:
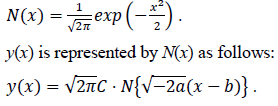
Estimated total number of infected persons are represented by two zero point of the logarithmic quadratic function above and Q(x), the cumulative distribution function of the normal distribution, as follows:
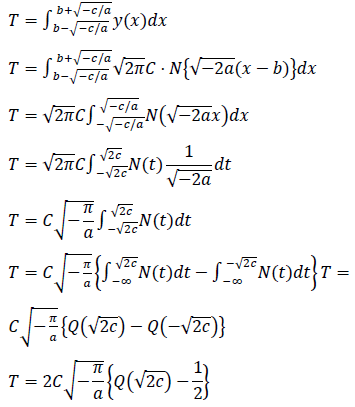
2.2.2 GLM and exponential model: The generalized linear model (GLM) for the epidemic count data introduces logarithmic transform as the link function and Poisson distribution for the residual distribution.
As the exponential regression, the function
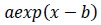
is fitted to the epidemic count data and logarithms of count data. The constant term is not introduced to let the tail of the model converge to zero. Parameter values of the logarithmic quadratic function and exponential regression can be found by iterative nonlinear optimization algorithms, such as Levenberg-Marquardt method or modified Powell method, however, it is necessary to give the algorithms initial parameter values that is close enough to optimal values to be found. Handiwork is often needed for good initial values. Numerical optimization of the logarithmic quadratic function generally goes smoothly comparing with models that contain the exponential function.
3. Result
3.1 Tokyo
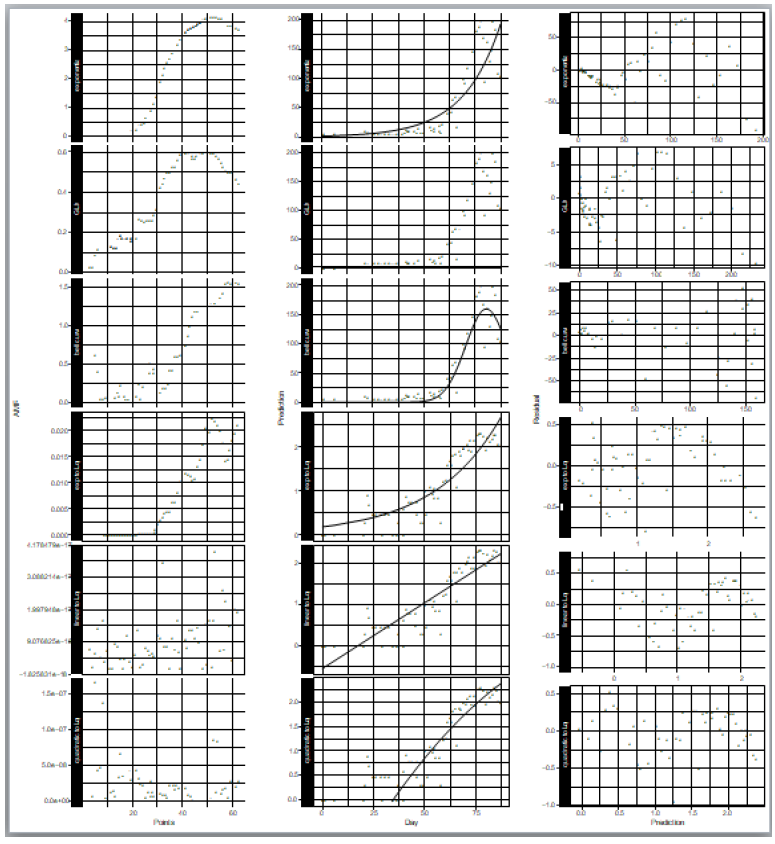
We applied the logarithmic quadratic function model to the daily epidemic count data of Tokyo, and compared statistical properties of the model with those of the exponential regression and GLM. The data published by Tokyo metropolitan government [7] were used for model comparison. This is the daily numbers of persons found infected in Tokyo from January 24, 2020, when the first infected person was confirmed in Tokyo, to April 20, 2020. The day on which the count is zero was excluded from the data. The analyzed data consist of 62 days. The epidemic count hardly increases in the former period of the Tokyo data, and it increases in the latter period (Figure 1, middle). The exponential regression, GLM, and the bell curve regression were applied to this count data, and the exponential regression, linear regression, and the quadratic polynomial function regression were applied to the logarithms of the count data. We introduced the Poisson distribution for the error distribution model and the logarithmic transformation for the link function of GLM.
We searched for the data range that gave the best fit for each model by reducing the samples (days) one by one from the beginning of the data. The model fitness was evaluated by the absolute value of the mean of the residuals of the data, AMR, defined as follows:
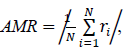
where N is the number of samples in the count data, ri is the residual of the sample i and the expected value for the sample i that is predicted by the fitted model. In the AMR plot (Figure 1, left) of the logarithmic quadratic model, N for which the fit is optimal can be roughly seen, the minimum is at N = 49. In the linear model, AMR has little correlation with N. Other models have the lowest AMR when the data size is reduced to approximately 10 points or less. Therefore, except for the logarithmic quadratic model, the entire original data consist of 62 samples was used for model fitting, namely we chose N = 49 for the logarithmic quadratic function model and 62 for all other models.
In the distribution of residuals to the expected value predicted by the model (Figure 1, right), it is most vertically symmetrical when the bell curve is applied to the count data. Also in the logarithmic quadratic function model, which is a logarithmic version of the bell curve model for count data, the residual distribution is approximately vertically symmetrical. In other models, the residual is biased both upward and downward depending on the model prediction values.
Especially the going down profile in the right most part of the plots shows that the model prediction is too large for large count data. The fewer the outlier, the better generally in the distribution of leverages (Figure S1). It is customary for outliers to be at least 2.5 times the average value. In the modeling of the epidemic counts, the outliers are the most in the case of the exponential regression to the count data, and are the same as or larger than those of the models for logarithms of counts. In the modeling of the logarithms of counts, the number of outliers is the same in linear regression and the quadratic function regression, however, outliers and other samples are separated clearly in the plot of the linear regression. This separation is unnatural statistically.
3.2 Worldwide estimation
When the logarithmic quadratic function model is applied and the model curve is convex upward, the two points where the model curve intersects the horizontal axis (zero point) are found. These can be estimates of the starting and subsiding dates of an epidemic. The total number of infected persons can also be estimated by integrating the model function from the estimated starting date to the subsiding date. We applied the quadratic function to the logarithms of the epidemic counts in each country, observed in the period from the end of 2019 to April 17, 2020. The dataset is published by European Centre for Disease prevention and Control (ECDC) [8]. The number of countries or regions included is 204. For the fitting range, we searched for the range where the AMR was the smallest for each country. The number of countries and regions where the model was convex upward was 114. The estimations of starting and subsiding dates and the total number of infected persons were calculated for these. The numbers of days from the estimated starting date to the subsiding date, or estimated period of epidemic, of the top 30 countries are shown in Table 1. The estimated total numbers of infected persons of top 30 countries are shown in Table 2. Plots of logarithms of count data and model predictions for each country are shown in the supplementary.
When the size of data is small or epidemic counts are small for a country, the influence of data errors to model parameters is large, so parameter estimations are not reliable for such countries. Although the logarithmic quadratic function model was convex upward in 114 countries, 14 of them had a large relative AMR, and the fittings did not seem successful. The logarithmic quadratic function model of 33 countries became convex downward, and numerical calculation failed in 53 countries. Four countries (Anguilla, Bhutan, South Sudan and Yemen) were excluded from modeling because the daily epidemic counts are only 0 or 1.
Figure 1: Statistical properties of models that fitted to epidemic count data and logarithms of epidemic counts. Left) Model fitness vs data size, Middle) count data and model prediction, and Right) residuals vs model prediction values. Upper three rows are of models for count data and lower three are for logarithm of count data.
|
Estimated Days of Epidemic |
County |
|
278.3 |
Senegal |
|
258.5 |
San_Marino |
|
243.1 |
Peru |
|
210.0 |
Slovakia |
|
198.7 |
Russia |
|
175.7 |
Bahamas |
|
173.6 |
China |
|
159.3 |
Uzbekistan |
|
156.5 |
Saudi_Arabia |
|
132.2 |
Paraguay |
|
130.4 |
India |
|
117.1 |
Democratic_Republic |
|
114.4 |
Mexico |
|
112.9 |
Indonesia |
|
109.0 |
Sweden |
|
104.4 |
Uruguay |
|
104.1 |
Kazakhstan |
|
102.4 |
Italy |
|
101.4 |
Iran |
|
99.8 |
Serbia |
|
99.5 |
Morocco |
|
98.5 |
Ireland |
|
98.4 |
South_Korea |
|
97.3 |
Palestine |
|
97.2 |
Bulgaria |
|
96.1 |
Pakistan |
|
95.7 |
Brazil |
|
95.2 |
Algeria |
|
92.3 |
Cote_dIvoire |
|
91.9 |
Finland |
Table 1: Estimated period lengths in days of epidemic of top 30 counties those relative AMR is less than 0.03.
|
Estimated Number of Total Cases |
Country |
|
5636461.7 |
Russia |
|
4350695.2 |
Peru |
|
213335.6 |
Spain |
|
194503.7 |
Italy |
|
143654.2 |
Germany |
|
109365.7 |
India |
|
108111.5 |
Turkey |
|
92216.3 |
Iran |
|
75154.5 |
Saudi_Arabia |
|
64596.7 |
Brazil |
|
45299.1 |
Canada |
|
44709.0 |
Belgium |
|
37631.5 |
Netherlands |
|
29618.6 |
China |
|
28518.7 |
Switzerland |
|
25445.0 |
Mexico |
|
22857.1 |
Ireland |
|
21888.4 |
Uzbekistan |
|
21469.5 |
Portugal |
|
20065.4 |
Sweden |
|
14232.1 |
Pakistan |
|
14206.0 |
Serbia |
|
13816.9 |
Austria |
|
13653.6 |
Ukraine |
|
12723.2 |
Israel |
|
12722.4 |
Indonesia |
|
12121.0 |
Chile |
|
11503.3 |
Poland |
|
10784.4 |
Romania |
|
10297.4 |
Ecuador |
Table 2: Estimated final numbers of cases, or infected person counts of top 30 countries those relative AMR is less than 0.03.
4. Discussion
By searching the range of data for which the model is optimal, the logarithmic quadratic function with statistically better properties than the exponential function and GLM can be obtained. Optimal data ranges cannot be found for other models. It is commonly said that observations increase exponentially in an early period of an epidemic, that is, their logarithms look linear with time, but a regression model to capture the profiles of logarithms of epidemic count should be the quadratic polynomial function, rather than the linear. The bell curve model for the epidemic counts is mathematically equivalent to the quadratic polynomial model for the logarithms of the counts, but in the former, the predicted value decreases at the end of the data range, whereas it does not in the logarithmic quadratic model (Figure 1, middle). In the fitting results of the bell curve model, the error of the count data is large when the predicted value is large. It is considered that the sensitivity of the parameter value to the error is high due to the exponential function in the model, and this sensitivity caused overfitting. The logarithmic quadratic function is more suitable for parameter estimation because the numerical calculation for parameter estimation is stable generally and the run-time error is less likely to occur.
In general count data, such as the epidemic count data, the distribution of the counts and the residuals of the data may seem to be larger as the model prediction values are larger. However, GLM of the logarithmic link function and Poisson distribution, which have these characteristics, do not show that it has good properties in this study; the residual distribution do not seem uniform for model prediction values. The residual distribution of the logarithmic quadratic function model looks more uniform. This suggests that the logarithms of the epidemic counts are not linear with time. Although the linear model for logarithms has very small AMR, this is a good result, but the distribution is heavily biased by the model values. The logarithmic quadratic function model can be used to estimate the starting and the subsiding dates, and the total number of infected cases. This is not possible with the exponential regression and GLM, which are monotonically increasing models. Therefore, the logarithmic quadratic function model may be useful for predicting the kinetics of epidemic in its early period. These estimations may be informative for exploring the transition mechanism from epidemic to pandemic. The logarithmic quadratic function is a very simple model. When this fits well the epidemic data, it is likely that the kinetics or the mechanism of the epidemic is simple. In other words, there is no or unchanging effect of artificial control of the epidemic. In the case of COVID-19, the epidemic went very fast, so it is considered that there are not a few cases where the epidemics began to subside before the governmental response was effective. The logarithmic quadratic function does not fit well to American data (Figure S2). This is considered to be due to the national measures taken.
It is sometimes difficult to fit the exponential quadratic function as a bell curve model directly to the epidemic count data. In order to do this, the initial values of the parameter values given to the fitting algorithm must be close enough to the optimum values, and it is often necessary to manually find good initial values. Therefore, the exponential quadratic function is not suitable for systematically fitting models of many countries as in this study. There are errors in the count data and the model parameters are highly dependent on the errors. Therefore, the estimated starting and subsiding dates and the estimated total number of infected persons are highly affected by the errors, and reliability of the estimations cannot be guaranteed for any data. Also, the data may deviate from the "natural" quadratic curve if a national response is taken. We think it is needed to find a model that is more robust than the logarithmic quadratic function for such data.
5. Conclusions
We performed a regression analysis of the early period of the epidemic curve in Tokyo. Regressions for the daily number of infected persons with a linear model, a generalized linear model, and a regression with a quadratic exponential function (bell curve), and regressions with a linear model, a quadratic function, and a regression with a bell curve for the logarithm of the daily infected number were compared. As the result, the statistic properties of the quadratic function regression for logarithms (logarithmic quadratic function regression) was the best. We applied the logarithmic quadratic regression to country-specific data on the number of infected persons to estimate the length of epidemic period and the total number of infected persons. As a result, it was suggested that the logarithm of the epidemic curve deviates from the quadratic function due to governmental control.
Declarations
Ethics approval and consent to participate
'Ethics approval and consent to participate' are not applicable to this study because only data that are anonymized and published by governments were used.
Consent for publication
'Consent for publication' is not applicable to this study because only data that are anonymized and published by governments were used.
Availability of data and materials
All data analyzed during this study are published online by the Tokyo metropolitan government, Japan [7] and the European Centre for Disease prevention and Control (ECDC) [8]. These are included in supplementary information files of this published article. All data generated during this study are included in supplementary information files of this published article. All codes that were written for analyses in this study are included in supplementary information files of this published article.
Competing interests
The authors declare that they have no competing interests.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Authors' contributions
'Authors' contributions' is not applicable to this study because it is done solely by DT.
Acknowledgements
'Acknowledgements' is not applicable to this study.
References
- Kermack WO, McKendrick AG. A Contribution to the Mathematical Theory of Epidemics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 115 (1927): 700-721.
- Grassly NC, Fraser C. Mathematical models of infectious disease transmission. Nat. Rev. Microbiol (2008).
- Chowell G, Sattenspiel L, Bansal S, Viboud S. Mathematical models to characterize early epidemic growth: A Review. Phys Life Rev (2016).
- Vynnycky E, White RG. An Introduction to Infectious Disease Modelling. An introductory book on infectious disease modelling and its applications. U.S.A.: Oxford University Press (2010).
- Anderson RM, Heesterbeek H, Klinkenberg D, Hollingsworth TD. How will country-based mitigation measures influence the course of the COVID-19 epidemic?. The Lancet 395 (2020): 931-934.
- Beckerman AP, Childs DZ, Petchey OL. Getting Started with Generalized Linear Models. In: Beckerman AP, Childs DZ, Petchey OL, Getting Started with R An Introduction for Biologists, 2nd ed. U.S.A.: Oxford University Press (2017): 167-202.
- Latest updates on COVID-19 in Tokyo (2020).
- Download today’s data on the geographic distribution of COVID-19 cases worldwide (2020).
- Ma J. Estimating epidemic exponential growth rate and basic reproduction number. Infectious Disease Modelling 5 (2020): 129e141.
- Riazoshams AH, Habshah BM Jr, Mohamad Bakri Adam C. On the outlier Detection in Nonlinear Regression. International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering (2009).
- Marquardt DW. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. Journal of the Society for Industrial and Applied Mathematics 11 (1963): 431-441.
Supplementary
Figures
Codes
Code 1: GNU R script for Tokyo data analysis
#
# the URL of the epidemic count data of Tokyo to be analyzed #
# https://stopcovid19.metro.tokyo.lg.jp/data/130001_tokyo_covid19_patients.csv
library(tidyverse); library(ggfortify); library(gridExtra); rm(list=ls());
std <- function(x0) { y <- x0;
x <- x0[!is.na(x0)];
y[which(!is.na(x0))] <- x - mean(x)/sd(x); y;
}

N <- length(DAYS);
cases <- data.frame(rep(NA, N), rep(NA, N), rep(NA, N));
colnames(cases) <- c("day", "cases", "log"); i <- 1;
for (day in DAYS) {

if (x > 0) { cases[i, ] <- c(d, x, log10(x)) } i <- i + 1;
}
cases <- cases[!is.na(cases$day), ]; N <- dim(cases)[1];
thm <- theme_linedraw(); #theme_bw(); plot(cases[, 1], cases[, 2]);
# fit exponential curve
coef0 <- list(a = 0.0746120, b = 0.1002581);
aic <- data.frame(matrix(rep(NA, (N-2)*2), ncol = 2)); colnames(aic) <- c("Points", "AIC");
for (i in 1:(N-2)) {
dat <- cases[i:N, ]; aic[i, 1] <- dim(dat)[1];
model <- try(nls(cases ~ a*exp(b * day), data = dat, start = coef0)); if (class(model) == "nls") { aic[i, 2] <- abs(mean(residuals(model))) }
}
amrs_ex <- aic; colnames(amrs_ex) <- c("days", "AIC_ex") dat <- cases[which.min(aic[,2]):N, ];
dat <- cases;
model <- try(nls(cases ~ a*exp(b * day), data = dat, start = coef0)); pred_ex <- predict(model);
resd_ex <- residuals(model); V <- model$m$gradient();
leve_ex <- diag(V %*% solve(t(V) %*% V) %*% t(V)); pdat_ex <- data.frame(dat, pred_ex, resd_ex, leve_ex);
# fit bell curve
coef0 <- list(a = 200, b = 100, c = 400);
aic <- data.frame(matrix(rep(NA, (N-2)*2), ncol = 2)); colnames(aic) <- c("Points", "AIC");
for (i in 1:(N-2)) {
dat <- cases[i:N, ]; aic[i, 1] <- dim(dat)[1];
model <- try(nls(cases ~ a*exp(-((day - b)^2)/c), data = dat, start = coef0)); if (class(model) == "nls") { aic[i, 2] <- abs(mean(residuals(model))) }
}
amrs_be <- aic; colnames(amrs_be) <- c("days", "AIC_be") dat <- cases[which.min(aic[,2]):N, ];
dat <- cases;
model <- try(nls(cases ~ a*exp(-((day - b)^2)/c), data = dat, start = coef0)); pred_be <- predict(model);
resd_be <- residuals(model); V <- model$m$gradient();
leve_be <- diag(V %*% solve(t(V) %*% V) %*% t(V)); pdat_be <- data.frame(dat, pred_be, resd_be, leve_be);
# fit Generalized Linear Model (log and poisson) coef0 <- list(a = -10, b = 30, c = 10);
aic <- data.frame(matrix(rep(NA, (N-2)*2), ncol = 2)); colnames(aic) <- c("Points", "AIC");
for (i in 1:(N-2)) {
dat <- cases[i:N, ]; aic[i, 1] <- dim(dat)[1];
model <- glm(cases ~ day, data = dat, family = poisson);
if (class(model) == "glm") { aic[i, 2] <- abs(mean(residuals(model))) }
}
amrs_gl <- aic; colnames(amrs_gl) <- c("days", "AIC_gl") dat <- cases[which.min(aic[,2]):N, ];
dat <- cases;
model <- glm(cases ~ day, data = dat, family = poisson); cat("2.5 x mean(leverage) =", 2.5*2/length(cases$cases), "\n") pred_gl <- predict(model);
resd_gl <- residuals(model); leve_gl <- hatvalues(model);
pdat_gl <- data.frame(dat, pred_gl, resd_gl, leve_gl);
# fit to log of epidemic count data
# fit exponential curve to log of epidemic counts coef0 <- list(a = 0.1, b = 0.1);
aic <- data.frame(matrix(rep(NA, (N-2)*2), ncol = 2)); colnames(aic) <- c("Points", "AIC");
for (i in 1:(N-2)) {
dat <- cases[i:N, ]; aic[i, 1] <- dim(dat)[1];
model <- try(nls(log ~ a*exp(b * day), data = dat, start = coef0));
if (class(model) == "nls") { aic[i, 2] <- abs(mean(residuals(model))) }
}
amrs_exL <- aic; colnames(amrs_exL) <- c("days", "AIC_exL") dat <- cases[which.min(aic[,2]):N, ];
dat <- cases;
model <- try(nls(log ~ a*exp(b * day), data = dat, start = coef0)); pred_exL <- predict(model);
resd_exL <- residuals(model); V <- model$m$gradient();
leve_exL <- diag(V %*% solve(t(V) %*% V) %*% t(V)); pdat_exL <- data.frame(dat, pred_exL, resd_exL, leve_exL);
# Linear model to log of epidemic counts coef0 <- list(a = 6, b = 138, c = 3856);
aic <- data.frame(matrix(rep(NA, (N-2)*2), ncol = 2)); colnames(aic) <- c("Points", "AIC");
for (i in 1:(N-2)) {
dat <- cases[i:N, ]; aic[i, 1] <- dim(dat)[1];
model <- lm(log ~ day, data = dat);
if (class(model) == "lm") { aic[i, 2] <- abs(mean(residuals(model))) }
}
amrs_glL <- aic;
dat <- cases[which.min(aic[,2]):N, ]; dat <- cases;
model <- lm(log ~ day, data = dat); pred_glL <- predict(model); resd_glL <- residuals(model); leve_glL <- hatvalues(model);
pdat_glL <- data.frame(dat, pred_glL, resd_glL, leve_glL);
# fit quadratic curve to log of epidemic counts coef0 <- list(a = 6, b = 138, c = 3856);
aic <- data.frame(matrix(rep(NA, (N-2)*2), ncol = 2)); colnames(aic) <- c("Points", "AIC");
for (i in 1:(N-2)) {
dat <- cases[i:N, ]; aic[i, 1] <- dim(dat)[1];
model <- nls(log ~ a*(day - b)^2 + c, data = dat, start = coef0); if (class(model) == "nls") {
#aic[i, 2] <- AIC(model) ;
#aic[i, 2] <- mean(log(dnorm(residuals(model)))); # RMSE aic[i, 2] <- abs(mean(residuals(model)));
#aic[i, 2] <- mean(abs(residuals(model))); # mean absolute error
}
}
amrs_quL <- aic;
NN <- which.min(aic[,2]) - 1;
dat <- cases[which.min(aic[,2]):N, ]; #dat <- cases;
model <- nls(log ~ a*(day - b)^2 + c, data = dat, start = coef0); pred_quL <- c(rep(NA, NN), predict(model));
resd_quL <- c(rep(NA, NN), residuals(model)); V <- model$m$gradient();
leve_quL <- c(rep(NA, NN), diag(V %*% solve(t(V) %*% V) %*% t(V))); pdat_quL <- data.frame(cases, pred_quL, resd_quL, leve_quL);
# make plots # AMR
damrs_ex <- cbind(amrs_ex, rep("exponential" )); colnames(damrs_ex) <- c("Points", "AMR", "Model");
damrs_gl <- cbind(amrs_gl, rep("GLM" )); colnames(damrs_gl) <- c("Points", "AMR", "Model");
damrs_be <- cbind(amrs_be, rep("bell curve" )); colnames(damrs_be) <- c("Points", "AMR", "Model");
damrs_exL <- cbind(amrs_exL, rep("exp to Log" )); colnames(damrs_exL) <- c("Points", "AMR", "Model");
damrs_glL <- cbind(amrs_glL, rep("linear to Log" )); colnames(damrs_glL) <- c("Points", "AMR", "Model");
damrs_quL <- cbind(amrs_quL, rep("quadratic to Log")); colnames(damrs_quL) <- c("Points", "AMR", "Model");
d_amr <- rbind(damrs_ex, damrs_gl, damrs_be, damrs_exL, damrs_glL, damrs_quL);
p_AMR <- ggplot(d_amr, aes(x = Points, y = AMR)) + thm + geom_point() + facet_grid(Model ~ ., scales = "free", switch = "y");
# plots of data and model curves
ddata_ex <- cbind(cases[,c(1,2)], pred_ex, rep("exponential" )); colnames(ddata_ex) <- c("Day", "Count", "Prediction", "Model"); ddata_gl <- cbind(cases[,c(1,2)], pred_gl, rep("GLM" )); colnames(ddata_gl) <- c("Day", "Count", "Prediction", "Model"); ddata_be <- cbind(cases[,c(1,2)], pred_be, rep("bell curve" )); colnames(ddata_be) <- c("Day", "Count", "Prediction", "Model"); ddata_exL <- cbind(cases[,c(1,3)], pred_exL, rep("exp to Log" )); colnames(ddata_exL) <- c("Day", "Count", "Prediction", "Model"); ddata_glL <- cbind(cases[,c(1,3)], pred_glL, rep("linear to Log" )); colnames(ddata_glL) <- c("Day", "Count", "Prediction", "Model"); ddata_quL <- cbind(cases[,c(1,3)], pred_quL, rep("quadratic to Log")); colnames(ddata_quL) <- c("Day", "Count", "Prediction", "Model");
d_mdl <- rbind(ddata_ex, ddata_gl, ddata_be, ddata_exL, ddata_glL, ddata_quL); p_MDL <- ggplot(d_mdl) + thm +
geom_line(aes(x = Day, y = Prediction)) + geom_point(aes(x = Day, y = Count)) + facet_grid(Model ~ ., scales = "free", switch = "y");
# plots of models and residuals
dresd_ex <- data.frame(pred_ex, resd_ex, rep("exponential" ));
colnames(dresd_ex) <- c("Prediction", "Residual", "Model");
dresd_gl <- data.frame(exp(pred_gl), resd_gl, rep("GLM" ));
colnames(dresd_gl) <- c("Prediction", "Residual", "Model");
dresd_be <- data.frame(pred_be, resd_be, rep("bell curve" ));
colnames(dresd_be) <- c("Prediction", "Residual", "Model");
dresd_exL <- data.frame(pred_exL, resd_exL, rep("exp to Log" ));
colnames(dresd_exL) <- c("Prediction", "Residual", "Model");
dresd_glL <- data.frame(pred_glL, resd_glL, rep("linear to Log" ));
colnames(dresd_glL) <- c("Prediction", "Residual", "Model");
dresd_quL <- data.frame(pred_quL, resd_quL, rep("quadratic to Log")); colnames(dresd_quL) <- c("Prediction", "Residual", "Model");
d_resd <- rbind(dresd_ex, dresd_gl, dresd_be, dresd_exL, dresd_glL, dresd_quL); p_RSD <- ggplot(d_resd, aes(x = Prediction, y = Residual)) + thm +
scale_y_continuous(limits = NULL) +
geom_point() + facet_wrap(Model ~ ., scales = "free", strip.position = "left", ncol = 1);
# leverage
dleve_ex <- data.frame(std(resd_ex) , leve_ex , rep("exponential" )); colnames(dleve_ex) <- c("StdResidual", "Leverage", "Model");
dleve_gl <- data.frame(std(resd_gl) , leve_gl , rep("GLM" )); colnames(dleve_gl) <- c("StdResidual", "Leverage", "Model");
dleve_be <- data.frame(std(resd_be) , leve_be , rep("bell curve" )); colnames(dleve_be) <- c("StdResidual", "Leverage", "Model");
dleve_exL <- data.frame(std(resd_exL), leve_exL, rep("exp to Log" )); colnames(dleve_exL) <- c("StdResidual", "Leverage", "Model");
dleve_glL <- data.frame(std(resd_glL), leve_glL, rep("linear to Log" )); colnames(dleve_glL) <- c("StdResidual", "Leverage", "Model");
dleve_quL <- data.frame(std(resd_quL), leve_quL, rep("quadratic to Log")); colnames(dleve_quL) <- c("StdResidual", "Leverage", "Model");
d_leve <- rbind(dleve_ex, dleve_gl, dleve_be, dleve_exL, dleve_glL, dleve_quL); p_LEV <- ggplot(d_leve, aes(x = Leverage, y = StdResidual)) + thm +
scale_y_continuous(limits = NULL) + ylab("Standardized Residual") + geom_point() + facet_wrap(Model ~ ., scales = "free", strip.position = "left",
ncol = 1);
Code 2: GNU R script for world wide data # The URL of the data to be analyzed
#
# https://www.ecdc.europa.eu/en/publications-data/download-todays-data- geographic-distribution-covid-19-cases-worldwide
rm(list = ls()); library(tidyverse); library(ggfortify);
thm <- theme_linedraw();
pdf(file = "covid19_ts_quad_opt_plots.pdf", width = 5, height = 5); erf <- function(x) 2 * pnorm(x * sqrt(2)) - 1;
data <- read.csv("csv/csvR020421.csv"); # the file of the downloaded data data <- mutate(data, dateRep = as.Date(dateRep, "%d/%m/%Y"));
data <- mutate(data, code = as.factor(countryterritoryCode)); country <- data.frame(data[, c(7, 9)]);
country <- distinct(country, countryterritoryCode, .keep_all = TRUE); country <- country[!is.na(country[2]), ];
rownames(country) <- country[, 2];
# extract national codes
N <- length(levels(data$code)) * 14;

colnames(pred) <- c("Points", "a", "b", "c", "AMR", "RAMR", "iter", "start", "peak day", "peak cases", "total cases", "end", "period", "plot"); rownames(pred) <- levels(data$code);
th <- 2; # days of count less than or equal to 2 are deleted for (ctry in levels(data$code)) {
if (ctry == "") { next } cat(ctry);
jpn <- data[data$countryterritoryCode == ctry, ]; jpn <- jpn[!is.na(jpn$dateRep), ];
dat <- jpn;
N <- length(dat$dateRep);
if (N < 9) { next } # data ignored if the number of days is less than 9
if (max(dat$cases) < th) { next } # yd <- dat$cases;
td <- dat$dateRep - as.Date("2019-12-01"); p0 <- 1;
rmse0 <- 1e308; rel0 <- 1e308; min_i <- 0; plotted <- FALSE; for (i in 1:(N-7)) {
y0 <- dat$cases;
t0 <- dat$dateRep - as.Date("2019-12-01"); y <- log10(y0[(y0 - th) > 0]);
t <- as.numeric(t0[(y0 - th) > 0]); if (length(y) < 9) { next }
a0 = -10; b0 = t[length(t)]; c0 = max(y);
Mdl <- try(nls(y ~ a*(t-b)^2+c, start = c(a = a0, b = b0, c = c0))); if (class(Mdl) == "nls") {
#rmse <- sqrt(mean(residuals(Mdl)^2)); rmse <- abs(mean(residuals(Mdl)));
#rmse <- abs(mean(residuals(Mdl)/predict(Mdl))); rel <- abs(mean(residuals(Mdl)/predict(Mdl))); if ((coef(Mdl)[1] > 0) && (coef(Mdl)[3] > 0)) {
pred[ctry, ] <- c(length(y), coef(Mdl)[1], coef(Mdl)[2], coef(Mdl)[3], rmse, rel, i, NA, NA, NA, NA, NA, NA, NA);
next;
}
if ((rmse >= rmse0) || (i == (N-7))) {
dat <- jpn[1:(length(jpn[, 1]) - min_i + 1), ]; y0 <- dat$cases;
t0 <- dat$dateRep - as.Date("2019-12-01"); y <- log10(y0[(y0 - th) > 0]);
t <- as.numeric(t0[(y0 - th) > 0]);
a0 = -10; b0 = t[length(t)]; c0 = max(y);
Mdl <- try(nls(y ~ a*(t-b)^2+c, start = c(a = a0, b = b0, c = c0)));
c("t");
rel <- abs(mean(residuals(Mdl)/predict(Mdl)));
a <- coef(Mdl)[1]; b <- coef(Mdl)[2]; c <- coef(Mdl)[3]; srt <- NA; end <- NA; per <- NA; tot <- NA;
if (a < 0) {
srt <- b - sqrt(-c/a); end <- b + sqrt(-c/a); per <- end - srt;
#new_t <- data.frame(round(srt):round(end)); colnames(new_t) <-
#tot <- sum(10^predict(Mdl, new_t));
tot <- 10^c * sqrt(-pi/(a*log(10))) * 2 * (pnorm(sqrt(2*c)) - 0.5);
} else {
if (c < 0) { srt <- b + sqrt(-c/a) }
}
pred[ctry, ] <- c(length(y), a, b, c, rmse0, rel0, i, srt, b, 10^c, tot, end, per, "fitted");
if (a > 0) break; td <- td[yd >= th];
yd <- log10(yd[yd >= th]);# yd[!is.finite(yd)] <- -0.5;
plot(td, yd, type = "p", xlab = "days", ylab = "log10 of cases", main = country[country$countryterritoryCode == ctry, 1]);
points(t, y, pch = 20); lines(t, y);
#legend("topleft", legend = country[country$countryterritoryCode == ctry, 1]);
mtext(sprintf("relarive AMR = %8.6g", rel0), side = 3, line = -1, adj =
0.05);
}
plotted <- TRUE; cat(": fitted.\n");
p_t <- seq(from = max(t), to = srt, by = -1); f <- predict(Mdl, list(t = p_t));
lines(p_t, f, col = "gray", lwd = 3);
#if (rel > 0.03) { lines(p_t, f, col = "red", lwd = 3) } #else { lines(p_t, f, col = "gray", lwd = 3) }
break;
else { rmse0 <- rmse; rel0 <- rel; min_i <- i }
}
if ((length(jpn[, 1]) - i) < 1) { break }
dat <- jpn[1:(length(jpn[, 1]) - i), ];
}
if (!plotted) {
yd <- dat$cases;
td <- dat$dateRep - as.Date("2019-12-01"); td <- td[yd >= th];
yd <- log10(yd[yd >= th]);# yd[!is.finite(yd)] <- -0.5;
plot(td, yd, type = "p", xlab = "days", ylab = "log10 of cases", main = country[country$countryterritoryCode == ctry, 1]);
points(t, y, pch = 20); cat(": failed to fit\n");
pred[ctry, "plot"] <- "plotted";
}
}
dpred <- data.frame(pred, country$countriesAndTerritories); colnames(dpred)[dim(dpred)[2]] <- "nation";
for (i in 1:length(dpred[, 1])) { code <- rownames(dpred)[i]; nation <- NA;
for (j in 1:length(country[, 1])) { if (country[j, 2] == code) nation <- country[j, 1] }
dpred[i, "nation"] <- nation;
}
write.csv(dpred, file = "covid19_ts_quad_opt.csv");
dev.off();
Data
https://www.fortunejournals.com/supply/acbr_4104/data/file1.xlsx
https://www.fortunejournals.com/supply/acbr_4104/data/file2.xlsx







 Impact Factor: * 5.8
Impact Factor: * 5.8 Acceptance Rate: 71.20%
Acceptance Rate: 71.20%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 