Predictive Model of COVID-19 Incidence and Socioeconomic Description of Municipalities in Brazil
Isadora CR Carneiro1,¶, Eloiza KGD Ferreira1,¶, Janaina C da Silva2,¶, Guilherme Soares1,3, Daisy M. Strottmann4, Guilherme F. Silveira*,1
1Carlos Chagas Institute - Fiocruz/PR, Curitiba, PR, Brazil
2Tumor Biology Laboratory, State University of Western Paraná, UNIOESTE, Francisco Beltrão-PR, Brazil
3Reference Laboratories in Emerging and Reemerging Viruses, Instituto Carlos Chagas - Fiocruz/PR, Curitiba, PR, Brazil
4Molecular Virology Laboratory, Instituto Carlos Chagas - Fiocruz/PR, Curitiba, PR, Brazil
¶These authors contributed equally to this study
*Corresponding author: Guilherme F. Silveira, Carlos Chagas Institute - Fiocruz/PR, Curitiba, PR, Brazil
Received: 25 February 2022; Accepted: 04 March 2022; Published: 10 March 2022
Article Information
Citation:
Isadora CR Carneiro, Eloiza KGD Ferreira, Janaina C da Silva, Guilherme Soares, Daisy M. Strottmann, Guilherme F. Silveira. Predictive Model of COVID-19 Incidence and Socioeconomic Description of Municipalities in Brazil. Fortune Journal of Health Sciences 5 (2022): 110-125.
View / Download Pdf Share at FacebookAbstract
Introduction
A new highly contagious coronavirus termed severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) emerged in China, in December 2019. The virus has spread rapidly, reaching all continents around the world, causing a potentially lethal human respiratory infection, COVID-19. Despite being the best alternative in the current pandemic context, social distancing measures alone may not be sufficient to prevent SARS-CoV-2 spread, and the overall impact of the virus is of great concern.
Objectives
Herein, we describe the demographic and socioe-conomic characteristics of 672 cities with at least 1 reported case of COVID-19 until June 26, 2020, and thus, determine a predictive model for the number of cases using data from patients tested for SARS-CoV-2 and the autoregressive integrated moving average (ARIMA) approach.
Methods
Predict model and epidemiological study based on aggregated data from the recent COVID-19. The SARS-CoV-2 has spread around the world wider than any previous human viral disease over a century and to predict the dynamic risk of the disease into subnational regions we used a thorough exploratory data analysis of COVID-19 cases according to the sociodemographic Brazilian municipalities indicators and an autoregressive integrated moving average (ARIMA) model.
Results
Following the first case of COVID-19 in the country to the reporting period confirmed cases of the disease were present in cities of all Brazilian states, affecting 36.5% of the municipalities in Rio de Janeiro State. The inhabitants in cities with reported cases of COVID-19 represent more than 73.1% of the Brazilian population. Stratifying by age or gender groups of the inhabitants does not affect COVID-19 incidence (confirmed cases/100,000 inhabitants). The demographic density, the Municipal Human Development Index (MHDI) and the per
Keywords
<p>COVID-19; COVID-19 in Brazil; Exploratory data analysis; ARIMA; computational model</p>
Article Details
1. Introduction
A pandemic is defined as any epidemic disease widely distributed geographically that affects different regions simultaneously. Over the years, humanity has faced many instances when health and science are put to the test and need to present answers. The Spanish flu ravaged the whole world and was often confused with several other diseases, such as cholera, dengue, and typhus [1].
At the end of the pandemic, approximately 50 million people had died. In 2009, a novel influenza A (H1N1) virus emerged in Mexico, where the transmission remained geographically contained for at least one month. Migratory events and population movement caused the virus to spread to other countries, leading the World Health Organization (WHO) to declare H1N1 a global pandemic [2].
In official WHO records, the H1N1 pandemic resulted in the deaths of 18,500 people around the world. On March 11, 2020, after a declaration by the WHO, the world population again lived under a shadow of fear of a new pandemic, this time caused by a coronavirus (CoV). CoV are enveloped viruses that are part of a large family of single-stranded RNA viruses with a positive-sense genome and can cause respiratory, gastrointestinal, hepatic, and neurological diseases. CoV can infect many animal species, including birds, cows, pigs, and humans, causing acute and chronic diseases [3, 4]. Most infections caused by viruses from the family Coronaviridae induce a mild form of the disease in humans, usually causing flu- like symptoms. However, after the discovery of severe acute respiratory syndrome (SARS), a greater contagion capacity and lethality potential of this viral family was evidenced [4]. The etiological agent of SARS, SARS-CoV, was identified in mid-2003 after an outbreak of the disease in November 2002 in Guangdong Province, China, where 8,700 cases and 774 deaths were confirmed [5].
The so-called novel CoV, initially referred to as 2019-nCoV, was first described when a group of patients reported symptoms of pneumonia of unknown cause in Wuhan City, Hubei Province, China, in December 2019 [6]. On February 11, 2020, after phylogenetic and pathophysiological analyses, 2019- nCoV was officially named SARS-CoV-2 due to its similarity to SARS-CoV, as announced by the CoV Study Group (CSG) of the International Committee on Taxonomy of Viruses (ICTV), according to the 2015 WHO nomenclature guidelines [7].
The pathology caused by SARS-CoV-2 infection was termed COVID-19, characterized by a flu-like condition associated with fever and cough that can progress to pneumonia and dyspnea in more severe cases [8]. The incubation period of the disease varies from 2 to 14 days, and in approximately 80% of cases, infected individuals remain asymptomatic. However, unlike patients with influenza, viral transmission from asymptomatic individuals is possible [5].
In addition, according to Contini (2020) [5], the mechanism of contagion is direct, that is, through contact with respiratory fomites of infected people. Other studies show that SARS-CoV-2 can survive in the air for more than 3 hours and on surfaces such as plastics and metals for up to 3 days [9]. Currently, there are no vaccines to prevent the disease, reinforcing the need for prophylactic measures, namely, correct hand, environment and surface hygiene and social distancing. A previous study has shown that social distancing and other preventive measures alone may not be sufficient to prevent the spread of COVID-19, and the overall impact of the virus is of great concern [10]. It is also noteworthy that additional research is needed to help define the exact rates and mechanisms of person-to-person transmission, as well as to determine additional factors that can guide containment actions.
The internal and external logistic and transitory movements, as well as several other socioeconomic factors, can not only contribute to the understanding of viral spread but also assist in surveillance mea-sures and competent decision-making for regional health systems, where such analysis can (and should) be implemented to reduce the exponential growth rate of positive cases. Mathematical models using epidemiological surveillance data have been used to predict the early dynamics of transmission and spread of several infectious diseases [11,12].
Different approaches are being used to better understand the transmission dynamics of SARS-CoV-2 to inform pandemic prevention and control measures. Nonetheless, computerized mathematical modeling for forecasting the spread of COVID-19 cases remains a challenge [13]. In this context, the present study aims to analyze the demographic and socioeconomic characteristics of cities with COVID-19 cases, as well as to adjust a predictive model based on the incidence of the cumulative disease cases thus expanding the possibilities of minimizing the impact of the current outbreak at the micro- and macro regional levels.
2. Material and Methods
In the present work, an ecological study design was used; this method of epidemiological study helped us to generate hypotheses about possible asso-ciations between socioeconomic characteristics of the Brazilian municipalities and the COVID-19 incidence and fatality rate. For the exploratory data analysis (EDA) and the predictive model adjustment, Python programming language was used with several libraries specifically for this purpose. Along with Python, it was necessary to import different packages and libraries, the most used ones being pandas, NumPy and SciPy, with the function of organizing and structuring the data.
For statistical calculations, the stats models package was imported to analyze the time series and the autoregressive integrated moving average (ARIMA) model for the forecasts. The purpose of these methods is to fit the model to the data as well as possible. Matplotlib and Sea born were used to generate two-dimensional (2D) graphics. The project can be accessed through the GitHub page, https://github.com/gfsilveira/covid. The analyzed database contains data from 672 municipalities (12, 1% of the cities in Brazil) in the 26 states of the federation plus the Federal District.
The records of COVID-19 cases at the municipal level were obtained through daily updates from the Health Departments of the Federative Units com-piled by Álvaro Justen and his collaborators until June 26, 2020, available at https://brasil.io/dataset/covid19/caso.
Demographic and socioeconomic characteristics publicly available at the municipal level, such as population density, Municipal Human Development Index (MHDI), total area in km² and per capita income, were obtained from the Brazilian Institute of Geography and Statistics (IBGE) from the demographic census conducted in 2010. Data on the age range and sex distribution of the population were obtained from the 2015 census.
A data structure containing different age groups between 0 and 80+ years old from the IBGE 2015 census database was used. The age of residents in Brazilian municipalities was separated into groups of young (0 to 29 years), adults (30 to 64 years) and seniors (65+ years). This distribution grouped ages according to low risk (young), comorbidities risk (adults) and complications risk (seniors) from SARS-CoV-2.
The percentage of declared sex data (female/male) was also analyzed in cities with cases of COVID-19. In addition to data from the population, the number of cities with COVID-19 cases within each state was analyzed by the percentage of Brazilian municipalities/states with confirmed cases until June 26, 2020. Incidence (cases per 100,000 inhabitants) was analyzed according to demographic density (inhabitants/km²), Municipal Human Deve-lopment Index (MHDI), socioeconomic data (per capita income), age groups and sex ratios.
For the development of the predictive model, we used the ARIMA model proposed by Box & Jen-kins (1970) [22], which consists of developing and adjusting stationary or non-stationary linear models relative to an observed time series. The autoregressive (AR) component indicates that the variable of the time series is regressed on its own lagged values. The I (for "integrated") indicates that the data values have been replaced with the diff-erence between n+1 and n values, performed more than once.
The moving average (MA) is a calculation of data points by creating a series of averages of different subsets of full data. In the moving average, the regression error is a linear combination of various times in the past and error terms whose values occurred contemporaneously. The construction of the model was based on daily COVID-19 cases. To analyze the stationary condition of the time series in different orders, the augmented Dickey-Fuller (ADF) test was used. The null hypothesis of the ADF test is that the time series is non-stationary.
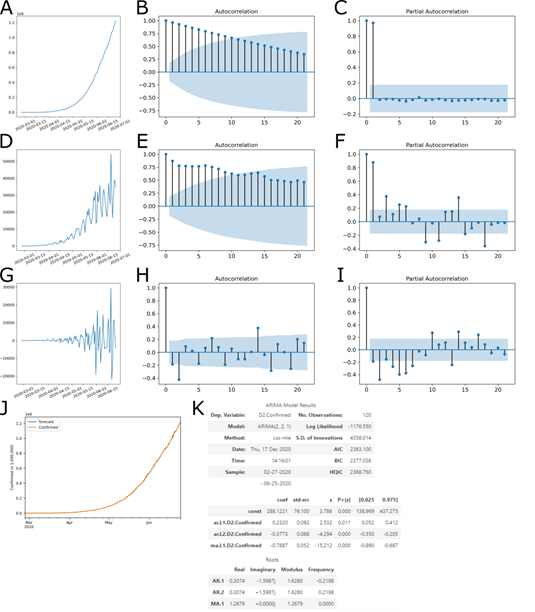
The p-value of the test was 0.000234, on the order of differentiation 2, less than the significance level (0.05), rejecting the null hypothesis and indicating that the time series is indeed stationary (Fig 1G). To determine which predictive model to use, the autocorrelation function (ACF) (Fig 1B, E, H) and partial autocorrelation function (PACF) (Fig 1C, F, I) were analyzed to determine the ARIMA p, d, and q parameters. The ACF is the correlation of a variable with itself at differing time lags, and the PACF partial autocorrelation at lag 1 is very high (it equals the ACF at lag 1), but the other values are correlated when lag > 1.
The PACF does not include any value for lag 0 because it is impossible to remove any intermediate autoco-rrelation between t and t−k when k=0, and therefore the PACF does not exist at lag 0. The ACF for an AR(p) process approaches zero very slowly, but the PACF goes to zero for values of lag > p. The ACF for an MA(q) process goes to zero for values of lag > q, but the PACF approaches zero very slowly. As defined by the ADF test, d = 2 was a second order of differentiation, making the series stationary (Fig 1G compared to Fig 1A and 1D).
In the second order of differentiation, the PACF with lag 2 is already below significance (Fig 1I), p = 1. The same occurs in the ACF in the second order, where lag 2 is below significance (Fig 1H). Then, the parameters were tested by the minor Akaike Information Criteria (AIC), four ARIMA models, (1,2,0), (1,2,1), (2,2,0), (2,2,1) and (2,2,2). With these data, the ARIMA 215 parameters (2,2,1) showed the best adjustment (Fig 1J).
Figure 1: ACF and PACF Plots for Determination of Model Parameters. (A-C) Original series, (D-E) 1st-order differencing and (G-I) 2nd-order differencing. (A, D and G) Time series, with number of cases by date; (B, E and H) autocorrelation function; and (C, F and I) partial autocorrelation function. With this data, a model ARIMA (p=2, d=2, q=1) was determined. (J) Adjustment of forecast data with observed outcome data. (K) Summary of coefficients of the ARIMA model.
3. Result
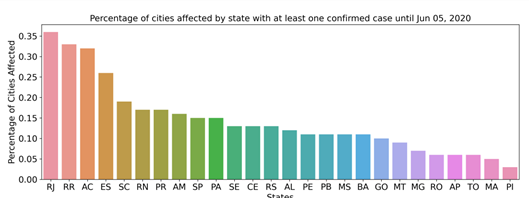
A total of 73.1% of the Brazilian population lives in cities with confirmed cases of COVID-19. Since COVID-19 is a pathology caused by SARS-CoV-2 that is transmitted directly from person to person we seek to observe the characteristics of the affected cities. The analyzed database contains data from 672 municipalities (12.1% of the 5,570 cities in Brazil) from the 26 states of the federation, plus the Federal District (Fig 2), which had at least 1 confirmed infection as of June 26, 2020, totaling 1,225,993 (0.58% of the Brazilian population) cases of COVID-19, which resulted in 54,918 deaths. The most affected state was Rio de Janeiro, reaching 36.5% of the municipalities reported cases of COVID-19. Until the last analyzed date, we observed an incidence rate of 63.31/100,000 inhabitants and a mortality rate of 2575 (per 100,000 inhabitants). The data analyzed in this work have been updated daily since February 25, 2020. The first 100 cases had been confirmed by March 14, and after one week, on March 21, there were already 1,000 confirmed cases. Brazil reached 10,000 and 100,000 confirmed cases on April 4 and May 3, respectively. As of Jun 19, the number of confirmed cases reached 1,039,339.
Distribution of confirmed cases of COVID-19 by state. Percentage of cities with at least 1 case of positive infection.
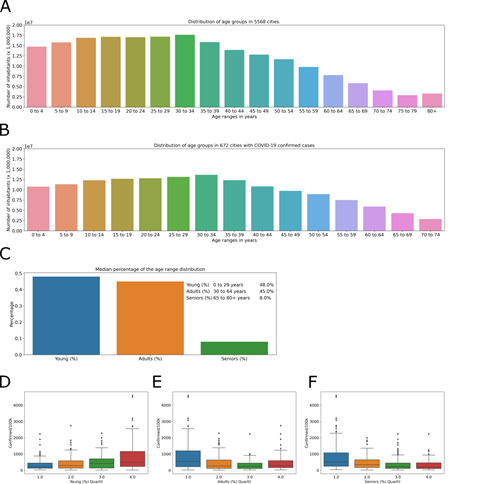
The population of Brazil in 2018 (last available data) was 210,147,125inhabitants, with the largest number of inhabitants between 10 and 34 years old (Fig 3A). The cities where cases of COVID-19 were observed have 153,528,953 inhabitants, representing 73.1% of the Brazilian population, and as expected, the distribution of age groups is the same as the general distribution in Brazil (Fig 3B). The direct comparison of the age group data (every 5 years) with the incidence of COVID-19 does not return positive correspondence (data not shown), thus, age groups were determined for a better comparison. The age ranges of the population in the affected cities were grouped into seniors over age 65, with a higher risk; adults between 30 and 64 with a greater likelihood of comorbidity; and the young, aged 0 to 29, with lower risk.
The percentage of inhabitants in each age group (Fig 3C) was be used for the analysis in relation to COVID-19 incidence. The city with the greatest incidence, Santo Antônio do Içá (Amazonas) (4592.17 cases/100,000 inhabitants), has 70% of inhabitants in the young group (0-29 years old), 27% in the adult group (30-64 years old) and 3% in the seniors group (65+ years old). In contrast, the city of Utinga (Bahia), with a lower COVID-19 incidence in the database (15, 64 cases/100,000 inhabitants), has 55% of inhabitants in the young group (0-29 years old), 38% in the adult group (30-64 years old) and 7% in the seniors group (65+ years old). The quartiles of the percentage of inhabitants in each age group were analyzed to determine if cities with a large percentage of senior, adult or young people have a greater incidence. For the young group, the percentage of inhabitants was divided into 34 – 44% (Fig 3D, blue), 45 – 48% (Fig 3D, orange), 49 – 51% (Fig 3D, green), and 52 – 71% (Fig 3D, red) of the total population. The adult group composed 26 – 41% (Fig 3E, blue), 42 – 45% (Fig 3E, orange), 46% (Fig 3E, green), and 47 – 52% (Fig 3E, red) of the total population. The senior group included 2 – 6% (Fig 3F, blue), 7 – 8% (Fig 3F, orange), 9 – 10% (Fig 3F, green), and 11 – 16% (Fig 3F, red) of the total population.
These groups were analyzed against the incidence of COVID-19 (Fig 2D-f). In young group, Tukey’s test shows no difference between quartile 1 and 2 (adjusted p = 0.496), 2 and 3 (adjusted p = 0.347) or 3 and 4 (adjusted p = 0.072). In adults group, Tukey’s test shows no difference between quartile 1 and 2 (adjusted p = 0.094), 2 and 3 (adjusted p = 0.4) or 3 and 4 (adjusted p = 0.51). And, in seniors group, Tukey’s test shows no difference between quartile 1 and 2 (adjusted p = 0.069), 2 and 3 (adjusted p = 0.421) or 3 and 4 (adjusted p = 0.9). In conclusion, in the affected cities, the age groups do not show a relationship with the incidence of the disease. Municipalities with a greater or lesser percentage of inhabitants in the young, adult, or senior age groups do not have a greater or lesser incidence of COVID-19.
Number of inhabitants by age group (increments of 5 years) in Brazil. Number of inhabitants by age group in cities with cases of COVID-19. Stratification of age groups by age in the municipalities studied, represented by the percentage of the number of inhabitants for each city (C). Distribution of quartiles of the number of inhabitants per age groups of (D) young, (E) adults, (F) seniors, in relation to the COVID-19 incidence, in the affected cities.
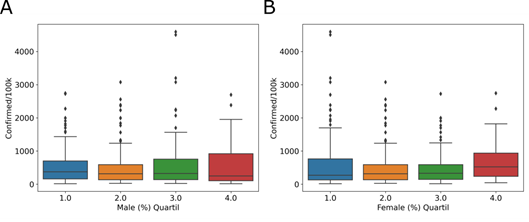
Another demographic factor analyzed was the declared sex of the inhabitants. In Brazil, the population distribution percentage is 51.7% for women and 48.3% for men. We observed a similar distribution, with 50.11% (2,979,950) women and 49.89% (2,965,800) men, in cities with COVID-19 cases. The quartiles of the number of women and men inhabitants in the affected cities do not show a relationship with the incidence of the disease. For the male group, 46 – 49% (Fig 4A, blue), 50% (Fig 4A, orange), 51% (Fig 4A, green), and 52 – 69% (Fig 4A, red) of the total population were included. For the female group, the percentage of inhabitants was divided into 31 – 49% (Fig 4B, blue), 50% (Fig 4B, orange), 51% (Fig 4B, green), and 52 – 54% (Fig 4B, red) of the total population. In male group, Tukey’s test shows no difference between quartile 1 and 2 (adjusted p = 0.9), 2 and 3 (adjusted p = 0.334) or 3 and 4 (adjusted p = 0.9). And, in female group, Tukey’s test shows no difference between quartile 1 and 2 (adjusted p = 0.313), 2 and 3 (adjusted p = 0.9) or 3 and 4 (adjusted p = 0.144). Municipalities with a greater or lesser number of men (Fig 4A) or women (Fig 4B) inhabitants do not have a greater or lesser incidence.
Distribution of quartiles of the percentage of (A) male and (B) female inhabitants, in relation to the COVID-19 incidence, in the affected cities.
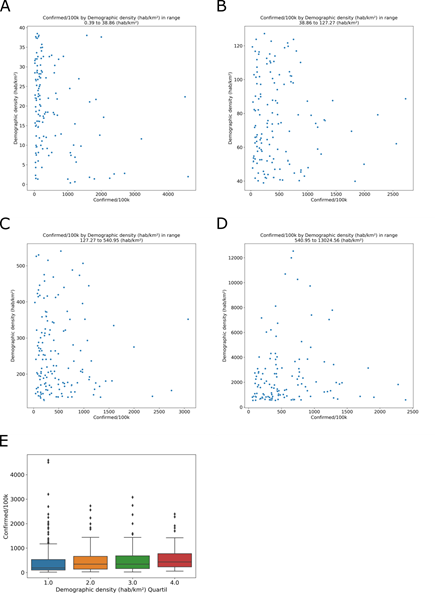
Since SARS-CoV-2 transmission can occur through close contact with infected people, we describe characteristics, of the dispersion and agglomeration of people in the municipalities, such as demographic density (inhabitants/km²). of the cities analyzed, 577 (86%) are more densely populated than the national average density, 23.9 hab/km². In the database, the mean population density was.76 hab/km² in all cities with COVID-19 cases. The city with the lowest demographic density was Novo Airão (Amazonas), with 0.39 hab/km² and 1074.33 cases/100,000 inhabitants. The highest demographic density was in São João de Meriti (Rio de Janeiro), with 13024.6 hab/km² and 334.881 cases/100,000 inhabitants. These apparent differences have no significance in the grouped data. The COVID-19 incidence was observed for the demographic density (hab/km²) quantiles, (Fig 5A) 0.39 to 38.86; (Fig 5B) 38.86 to 127.27; (Fig 311 5C) 127.27 to 540.95; and (Fig 5D) 540.95 to 13024.56. The analyses of the quartiles of demographic density show no relation with COVID-19 incidence (Fig 5E). In demographic density group, Tukey’s test shows no difference between quartile 1 and 2 (adjusted p = 0.9), 2 and 3 (adjusted p = 0.9) or 3 and 4 (adjusted p = 0.72). Municipalities with a greater or lesser demographic density do not have a greater or lesser incidence of COVID-19.
Number of inhabitants (population) by area (km²) resulting in demographic density (hab/km²) in four quantiles, (A) 0.39 to 38.86; (B) 38.86 to 127.27; (C) 127.27 to 540.95; and (D) 540.95 to 13024.56. (E) The relationship between the demographic density quartiles and COVID-19 incidence.
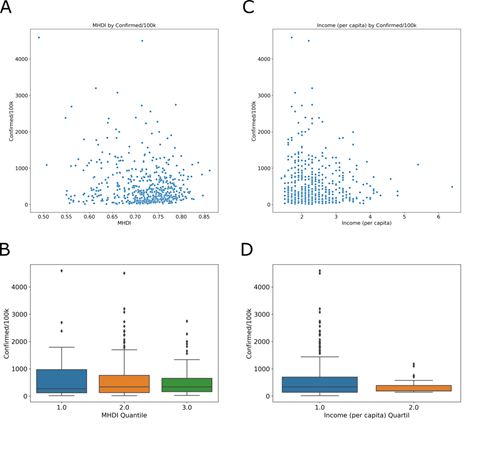
The Municipal Human Development Index (MHDI) is related to life expectancy, educational level and income distribution. The global Brazilian HDI for 2013 was 0.744, the 79th position in the world, ranking among the 187 countries and territories recognized by the United Nations. In the Global HDI for HDR 2014, the three dimensions have the same weight, and the human development ranges are fixed as follows: low human development, less than 0.550; average, between 0.550 and 0.699; high, between 0.700 and 0.799; and very high, above 0.800. In Brazil, the per capita income was 1.48 (R$ 1,443.10) for 2017 (last year with available data). In MHDI group, Tukey’s test shows no difference between quartile 1 and 2 (adjusted p = 0.648), 2 and 3 (adjusted p = 0.178). And, in income group, Tukey’s test shows no difference between quartile 1 and 2 (adjusted p = 0.066). In this context, the MHDI (Fig 6A) and per capita income (Fig 6C) were compared with COVID-19 incidence.
MHDI and (C) income (number of times the minimum wage [R$ 975.00] is earned per month for formal workers) in cities with cases of COVID-19. The relationship between the MHDI-low 0.49 to 0.613 (blue), MHDI- mean 0.614 to 0.737 (orange) and MHDI-high 0.738 to 0.862 (green) groups. (D) The income was divided into low 1.4 to 3.8 (blue) and high 3.9 to 6.4 (orange).
The results show that most cities with positive cases for COVID-19 are above the national average for both MHDI and per capita income. With the goal to observe the relationships in the data sets in greater detail, we analyzed the MHDI divided into low 0.49 to 0.613 (Fig 6B, blue), mean 0.614 to 0.737 (Fig 6B orange) and high 0.738 to 0.862 (Fig 6B, green) groups. The income was divided into low 1.4 to 3.8 (Fig 6D, blue) and high 3.9 to 6.4 (Fig 6D, orange). The socioeconomic index does not show a relationship with the incidence of the disease.
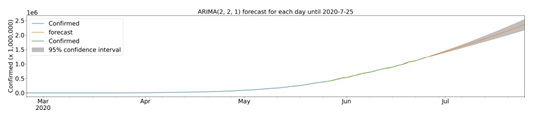
Once some of the characteristics of the cities with cases of COVID-19 were described, we sought to determine a model for predicting confirmed infection cases using the time series of officially reported infections. For July 25, 2020, the evolution model predicts 2,358,703 (2,172,930 to 2,544,477) confirmed cases. Due to the current level of infection in the cities analyzed, the scarcity of data does not allow the development of a robust predictive model for cases confirmed at the municipal level. To understand the condition of the infection at the national level, we analyzed the time series of accumulated data for confirmed cases. There was a clear upward trend in the number of cases (data not shown). To suggest a prediction for the evolution of COVID-19 cases in Brazil, we use computational modeling in the time series. The best adjusted model for the forecast was ARIMA (2,2,1) using data from the last 30 days, which forecasts 2,358,703 cumulative cases on July 25, 2020, with a 95% confidence interval of 2,544,477 to 2,172,930 (Fig 7). Analyzing the 30 days of predicted data compared to those obtained, we can obtain 19574.64 in Mean Absolute Error, 699036780.94 in Mean Squared Error, 0.000171 in Mean Squared Log Error, 15695.079 in Median Absolute Error and 0.99306 for R² (coefficient of determination).
ARIMA model of the forecast of confirmed cases until July 25, 2020. Confirmed cases (blue), forecast (orange), model fit analysis (green) and forecast with 95% confidence interval (gray). Up to the end date, between 2,544,477 and 2,172,930 cases are expected.
The work was deposited at medRxiv (doi https://doi.org/10.1101/2020.06.28.20141952), on June 29, 2020, which characterizes the present work as prospective. On July 25, 2020, the official case data was 2,394,513 [14], and in the database used as the source, Brasil.io was 2,337,647, so the proposed model was accurate above 98, 5% correct.
4. Discussion
In this work, we studied the recent occurrence of COVID-19, a respiratory disease caused by the coronavirus, SARS-CoV-2, which originated in the city of Wuhan, China, and analyzed the correlation of transmission and death rates, through confirmed cases using Brazilian demographic and socioeconomic data. Knowledge of the demographic distribution and socioeconomic situation of he population becomes significant when comparing transmission and death rates across the country.
Altogether, our data indicate that 672 cities, accounting for 73.1% of the Brazilian population, had at least 1 case of COVID-19 by June 26, 2020. The age distribution of the inhabitants in those cities, which include the most populous cities of Brazil, remains the same as the average age distribution of the Brazilian population. The average distribution of women and men in the cities studied also corresponds to the national average. The demographic density, the MHDI and the per capita income of the municipalities with cases of COVID-19 are above the national average. However, there seems to be no relationship between the indexes analyzed and the incidence of COVID-19 in these cities, suggesting that other factors (virulence, immune background) may influence the spread of the disease. Brazil currently has 5,570 municipalities in 26 states distributed disproportionately over a total area of 8,511,000 km² [15]. As described in the results section, municipalities with a population larger than 295,955 inhabitants showed a positive correlation between the size of the population and the number of confirmed cases of the disease. However, of all the municipalities, only 95 have a population of over 295,955 inhabitants, including all state capitals and the Federal District. The 95 municipalities most populous represent 1.71% of the country's total cities, with the majority, 94.22% (5,245 municipalities), of Brazilian cities having a population less than or equal to 100,000 inhabitants [15]. Therefore, based on our results, it is possible to assert that the transmission of the disease is more likely to impact less than 2% of Brazilian municipalities. However, it is essential to reinforce that the 95 most populous cities in the country, together, are home to 83,951,535 inhabitants, which represents 40% of the total population of Brazil, with a current demographic density of 205.5 million people [15]. Thus, neglecting the recommendations of the WHO about isolation and social conduct, in a time of a pandemic, is an attack on public health in Brazil.
When analyzing the data in relation to the states of the federation, we noted similar observations as those obtained in relation to the municipalities. The state of São Paulo is the most populous in the country and in turn is the state with the highest number of confirmed cases and death of COVID-19, acc-ording to the Ministry of Health (2020) [16]. It is important to note that the actual numbers of cases and deaths from the disease may be different from the official data, taking into account the impact that the delay in reporting has on the estimates and that reported cases depend on hospitalization [17]. One of the limitations in population-based epidem-iological studies is related to obtaining updated data, since many cases have been reported after the testing period. According to Martins (2020) Brazil faces problems with the supply of kits for the detection of COVID-19, in addition to few human resources trained to carry out tests, with delays in the release of results produced locally, causing delays in notification, and overload in reference laboratories and underreporting [18].
The novel coronavirus (SARS-CoV-2) emergency and the role of timely and effective national health surveillance. Cad Saúde Pública 2020; 36(3): e00019620 [10 p]. When we take into account the data obtained, it is possible to show that social isolation is a valid measure to be applied in munic-ipalities that have a resident population larger than 295,000 inhabitants. For these municipalities, the more intense the measures, the flatter the transmission curve becomes; thus, hospitals and health units can have greater control of the situation under the demand of patients who require specialized care.
However, it is important to mention that it is not possible to conclude the real importance of social isolation in municipalities with a population below the aforementioned number. Although, according to the results, there is a negative correlation between demographic density and the number of cases in these cities, which, in theory, would indicate a lack of connection between these aspects. According to Hellewell et al. (2012) [18], in a study to evaluate measures to contain the transmission of the disease, social isolation is insufficient to control the outbreak, requiring new interventions to achieve control of the transmission of the disease.
Time predictive models based on the incidence data collected represent important tools to analyze and predict the transmission process of infectious diseases. Indeed, our ARIMA model proved to be effective for predicting the evolution of the number of confirmed COVID-19 cases at national levels. Our model predicts 2,358,703 cumulative cases (2,172, 930 to 2,544,477) on July 25, 2020. Nevertheless, isolation can contribute to spreading the overall size of an outbreak over a longer period of time [18].
Taking this into account, it becomes possible to assess the importance of measures of social isolation, even for municipalities with a small population, demonstrating the great importance of such measures that should be intensified in the most populous cities and not neglected in cities with fewer than 295,000 inhabitants. Therefore, it is interesting to evaluate the average traffic of the Brazilian population mainly in the forms of essential workers, e.g., truck drivers, who supply basic necessities. This supply is primarily carried out in Brazil through land transportation, often long distance, between the capitals and other municipalities of the federation. During the month of March, an average of 1000 trucks arrived at the Supply Center of the Federal District every Monday and Thursday [19].
It would be interesting, as a future perspective, to further these studies in order to develop a system of equations that could indicate a proportional factor of the relationship between population and lethality rate to compare the fold-change in the lethality in a more populous city to that of a less populous city. Perhaps, as the number of inhabitants in a city doubles or triples, lethality does not necessarily double or triple, indicating that there is no linearity in the cases.
Therefore, the information reported in this study allows us to highlight that cities with a higher number of inhabitants who choose not to comply with social isolation have a higher risk and probability of infection. Besides, it is essential to show that infection with SARS-CoV-2 is not due to the simple fact of living in a more or less populous city and that there are different regional characteristics, both geographic and socioeconomic, that can influence dispersion, not only for SARS-CoV-2 but also for many other pathogens [20, 21]. Thus, it is worth emphasizing once again that in the current pandemic context, without effective prophylactic and therapeutic treatments, social isolation has proven to be an efficient measure to control outbreaks in the most populous cities.
Therefore, our findings suggest that this approach should indeed not just be simulated but also applied to reduce transmission and avoid hospital demands above service capacity, to provide care for all patients at the micro- and macro regional levels [17].
5. Conclusions
The data in the present work allow us to observe that until July 2020, it was not possible to observe correlations with some of the tested demographic data and the cases of COVID-19 in the Brazilian municipalities analyzed. The ARIMA model, used to determine the number of cases, was sufficient for a significant determination of cases in 30 days, showing that the present model can be used as a predictive tool in the present epidemiological conditions
Acknowledgments
We would like to thank Hellen Geremias dos Santos, PhD, for the critical reading of the work. We would like to thank the Creative Commons Attribution ShareAlike and Álvaro Justen and collaborators from Brazil. We thank IO for the confirmed case database. We would like to thank the scholarship funding agencies CAPES and Fiocruz.
References
- Goulart A da C. Revisitando a espanhola: a gripe pandêmica de 1918 no Rio de Janeiro. História, Ciências, Saúde-Manguinhos 12 (2005): 101–142.
- Lipsitch M, Finelli L, Heffernan RT, Leung GM, Redd SC. Improving the evidence base for decision making during a pandemic: the example of 2009 influenza A/H1N1. Biosecur Bioterror 9 (2011): 89–115.
- Chang H-W, Egberink HF, Halpin R, Spiro DJ, Rottier PJM. Spike Protein Fusion Peptide and Feline Coronavirus Virulence. Emerg Infect Dis 18 (2012): 1089–1095.
- Weiss SR, Leibowitz JL. Coronavirus pathogenesis. 1st ed. Advances in Virus Research 81 (2011): 85–164.
- Contini C, Nuzzo M Di, Barp N, Bonazza A, de Giorgio R, Tognon M, et al. The novel zoonotic COVID-19 pandemic: An expected global health concern. J Infect Dev Ctries 14 (2020): 254–264.
- Zhu N, Zhang D, Wang W, Li X, Yang B, Song J, et al. A novel coronavirus from patients with pneumonia in China, 2019. N Engl J Med 382 (2020): 727–733.
- Gorbalenya AE, Baker SC, Baric RS, de Groot RJ, Drosten C, Gulyaeva AA, et al. The species Severe acute respiratory syndrome-related coronavirus: classifying 2019-nCoV and naming it SARS-CoV-2. Nat Microbiol 5 (2020): 536–544.
- Chang T, Wu J, Chang L. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet 395 (2020): 514–523.
- Taylor D, Lindsay AC, Halcox JP. Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. N Engl J Med 382 (2020): 1564-1567.
- Sohrabi C, Alsafi Z, Neill NO, Khan M, Kerwan A. World Health Organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19). Int J Surg 76 (2020): 71-76.
- Valeri L, Patterson-Lomba O, Gurmu Y, Ablorh A, Bobb J, Townes FW, et al. Predicting subnational Ebola virus disease epidemic dynamics from sociodemographic indicators. PLoS One 11 (2016): 1–9.
- Kane MJ, Price N, Scotch M, Rabinowitz P. Comparison of ARIMA and Random Forest time series models for prediction of avian influenza H5N1 541 BMC Bioinformatics 15 (2014): 276.
- Anirudh A. Mathematical modeling and the transmission dynamics in predicting the Covid-19 - What next in combating the pandemic. Infect Dis Model 5 (2020): 366–374.
- Ministério da Saúde. Coronavírus COVID-19 2020 [cited 2020 July 25].
- Estimativas da população residente no brasil e unidades da federação com data de referência em 1o de julho de (2019). [cited 2020 July 24].
- Ministério da Saúde. Covid-19 no Brasil. (2020) [cited 2020 July 24].
- Dias J. InfoGripe destaca aceleração de internações por Síndrome Respiratória Aguda Grave (2020). [cited 2020 July 25].
- Hellewell J, Abbott S, Gimma A, Bosse NI, Jarvis CI, Russell TW, et Feasibility of controlling COVID-19 outbreaks by isolation of cases and 567 contacts. Lancet Glob Heal 8 (2020): e488–e496.
- Ceasa orienta caminhoneiros sobre a COVID-19 (2020) [cited 2020 July 25].
- Mogi R, Spijker J. The influence of social and economic ties to the spread of COVID-19 in Europe. SocArXiv [preprint] (2020) [cited 2020 July 24].
- Dowd JB, Andriano L, Brazel DM, Rotondi V, Block P, Ding X, et Demographic science aids in understanding the spread and fatality rates of COVID-19. Proc Natl Acad Sci U S A 117 (2020): 9696–9698.
- George Edward Pelham Box, Gwilym M. Jenkins GCR. Time Series Analysis Forecasting and Control. 5th ed. John Wiley & Sons (2015).


 Impact Factor: * 6.2
Impact Factor: * 6.2 Acceptance Rate: 76.33%
Acceptance Rate: 76.33%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 