The Use of Co-evolution to Model the Effects of Global Warming
C E Neal-Sturgess*
Emeritus Professor University of Birmingham UK
*Corresponding Author: CE Neal-Sturgess, Emeritus Professor University of Birmingham UK.
Received: 25 July 2023; Accepted: 03 August 2023; Published: 28 September 2023
Article Information
Citation: C E Neal-Sturgess. The Use of Coevolution to Model the Effects of Global Warming. Journal of Environmental Science and Public Health. 7 (2023): 160-163.
View / Download Pdf Share at FacebookAbstract
In their paper Natural selection for least action [1] depict evolution as a Path Integral process conforming to the Principle of Least Action (PLA). From this concept, an equation of motion for environmental coevolution was derived. Co-evolution [2] is a widespread phenomenon, as any system of coupled differential equations will conform to Co-evolution. Following this idea and the link to Path Integrals and PLA it is possible to generalise Co-evolution to any system of coupled differential equations such as Global Warming; that is what is done here. Taking an approximate approach to the Lagrangians involved gives a new simple metric defined as a “Coefficient of Impact” which reflects the importance of global warming on the particular effect, empirical evidence is used to calibrate the model; the results give similar levels of importance to other published values with the exception of the duration of heat waves.
Keywords
Coevolution, Natural selection, Climate
Article Details
Background
In their paper Natural selection for least action [1] depict evolution as a Path Integral process conforming to the Principle of Least Action (PLA), which is the one of the most fundamental physical principles in the Universe [3]. From this concept, together with the Coevolution model of Lewontin, [2] an equation of motion for environmental coevolution was derived [4] which shows that it is the time rate of change (frequency) of evolutionary change of the organism (mutations) that responds to changes in the environment. Co-evolution is a widespread phenomenon, and not just restricted to mutation rates in viruses, any system of coupled differential equations will conform to co-evolution. Following this idea and the link to Path Integrals and PLA it is possible to generalise co-evolution to any system of coupled differential equations such as Global Warming; that is what is done here. There have been earlier publications on the application of the path. integral method to climate change including: The Path Integral Formulation of Climate Dynamics by Antonio Navarra, J Tribbia, and Giovanni Conti [5]. This paper introduces the path integral formulation of climate dynamics and applies it to a simple model of the El Niño-Southern Oscillation (ENSO), and concentrates on the probability distributions of the variables; Path Integral Methods in Climate Dynamics by Mark Newman and Eric Vanden-Eijnden [6]. This book provides a mathematical overview of the path integral approach to climate dynamics, including applications to more complex models; Path Integrals in Climate Science by David J Wilson and Michael E. Fisher [7]. This book provides a m mathematical treatment of the path integral approach to climate dynamics, with a focus on the use of path integrals to study the chaotic behaviour of climate systems; Path Integrals for Climate Modelling by Daniel J Scheffler and Andreas W. Peters [8]. This book provides a practical guide to using the path integral approach to develop climate models, this concentrates on elastic-band models of solving path integral models. Starting with The Principle of Least Action and applying Noether’s Theorems [9] the conservation theorems can be derived, then depicting the evolution of the variable in Space-Time and applying Euler-Lagrange the unique trajectory in Space-Time can be derived. Applying this to Co-evolution gives;

defining the Lagrangians as

and applying Euler-Lagrange gives:
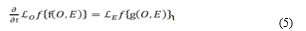
This is the fundamental equation defining co-evolution.
Then to generalise this principle to global warming gives:
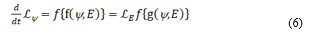
where the function depicts the impact on the effects of Global Warming
Although more work is required to define the Lagrangians at the highest level it is the sign of the right-hand side of the equation (6) that determines the sign of the derivative (frequency) on the left-hand side, and so if the sign of the right-hand side is positive then the frequency of the effects will increase.
It can be inferred that:

where GT is the Global Warming parameter with regional variations. Hence:
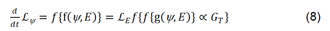
Hence the frequency of the effects of Global Warming are dependent on the gradient of the Global Warming parameter GT and as that parameter increases so does the frequency of the effects of Global Warming; this is the controlling equation of motion for the effects of climate change of global warming. The Lagrangians need defining, which is not an easy task [10,11] and often involves guesswork [10]. Lagrangians are essentially energy transfer functions and traditional Lagrangians in Classical Mechanics have involved the Potential and Kinetic energies of the system which, in conjunction with Euler-Lagrange defines the Least Action trajectory in Space-Time. Following the method used by [10] using the traditional approach it is necessary to define the Potential and Kinetic functions for the Lagrangians. The Potential function is difficult to define, but the kinetic function of the environmental Lagrangian can safely be assumed to be related to global warming (equation 8). The potential term is a function of the gravitational constant and can be assumed to be small and almost constant, which to a first approximation can be ignored. Hence the Lagrangians will be largely a function of the kinetic component only, so equation 8 can be rewritten as:

Hence,

If GT is defined as the change of Global warming over a specified period, and CI is defined as a Coefficient of Impact which represents the relative importance of global warming on the particular effect.
Results
In 2022 Neal-Sturgess showed that if the Classical Mechanics approach using the Principle of Least Action, expressing the system trajectory in Space-Time, and applying Euler-Lagrange using the Path Integral approach gives equation 4 which is the fundamental equation of species coevolution. In deriving this equation it became obvious that a similar derivation, but generalised, could apply to any system comprised of two sub-systems of two coupled differential equations; that is what is done here and applied to the effects of Global Warming. From the structure of Equation 8 it is obvious that if the slope (gradient) of the right-hand side of equation 8 is positive (increasing) with respect to time, then the left-hand side (frequency) of the observed effects will increase; this is the predominant effect of this analysis.
There is near Universal agreement that global warming is increasing [12], which means from equation 8 that the frequency of the effects is also increasing.
A detailed paper [13] considers 30 different effects of climate change. This shows that at the top level:
- Average annual temperature is increasing.
- Heat wave frequency is increasing, including:
- Major heat wave frequency
- Heat wave duration
- Hot-humid days
- River flood frequency is increasing.
All these factors and the rest of the 30 factors considered all increase in accordance with equation 8 and become worse as global temperature increases. To calibrate the model empirical evidence is used, the year 2000 is used as a baseline for convenience, and considering the top level for Europe gives: Global warming GT: The increase in global warming since 2000 has been significant. According to the National Oceanic and Atmospheric Administration (NOAA), the average global surface temperature has increased by 0.18°C (0.32°F) per decade since 2000; hence GT = 0.18. Mean increase in frequency of heat waves in Europe since 2000: According to a study published in the journal Nature Climate and Atmospheric Science, the mean increase in the frequency of heat waves in Europe since 2000 is 1.2 events per decade.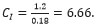
Duration of heat waves in Europe since 2000: According to a study published in the journal Nature Climate Change in 2020, the duration of heat waves in Europe has increased by an average of 10 days since 2000 (4 per decade) : hence 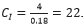
Increase in intensity of heat waves since 2000: According to the EPA's [14-16] Climate Change Indicators: Heat Waves report, the mean increase in the intensity of heat waves since 2000 is 0.3°F (0.17°C); hence 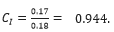 Increase in river flooding in Europe: A study by the European Environment Agency (EEA) found that the number of large river floods in Europe has increased by 150% since 1980. Normalising on the year 2000 to be comparable to the other metrics quoted, hence for large floods
Increase in river flooding in Europe: A study by the European Environment Agency (EEA) found that the number of large river floods in Europe has increased by 150% since 1980. Normalising on the year 2000 to be comparable to the other metrics quoted, hence for large floods 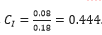
These results are broadly in the same order as identified by [13] with the exception of the duration of heat waves (CI = 22). There are an enormous number of references to the effects of Global Warming on the Web, to bring this up to date at the time of writing the last IPCC report was the 6th Report, now updated by the IPCC Synthesis Report March 2023. The recent IPCC Synthesis Report [IPCC sixth assessment report (ar6)] contains the results of 8 years of scientific research. Omitting the details, which are readily available in the report, the main points are below.
Observed Warming and its Causes
Observed Changes and Impacts
Current Progress in Adaptation and Gaps and Challenges
Current Mitigation Progress, Gaps and Challenges
None of the main and detailed findings of the IPCC Synthesis Report are in contradiction to the principal finding of this study that from the structure of Equation 8 it is obvious that if the slope (gradient) of the right-hand side of equation 8 is positive (increasing) with respect to time, then the left-hand side (frequency) of the observed effects will increase; this is the predominant effect of this analysis.
Conclusions
It has been shown that by using a Path Integral approach based on Least Action and using Euler-Lagrange a unique trajectory in Space-Time gives a controlling equation for Co-evolution which shows that if the gradient of global warming is positive then the frequency of the effects increases with time. A set of effects of climate change, concentrating on the major effects, all show that the controlling equation is validated. Taking an approximate approach to the Lagrangians involved gives a new simple metric defined as a “Coefficient of Impact” which reflects the importance of global warming on the particular effect; using empirical evidence the results give similar levels of importance to other published values, with the exception of the duration of heat waves (CI = 22).
References
- Kaila VRI, Annila A. Natural selection for least action. Proc R Soc A 464 (2008): 3055-3070.
- Levin R, Lewontin R. The dialectical Biologist. University of Harvard (1985).
- Nahin, PJ. When Least is Best, Princeton UP (2004).
- Neal-Sturgess. A Differential Equation for Mutation Rates in Environmental Coevolution. J Environ Sci Public Health (2022): 1-10.
- Navarra A, Tribbia J, Conti G. The Path Integral Formulation of Climate Dynamics. Plos one 8 (2013): e67022.
- Mark N, Eric Vanden-Eijnden. Path Integral Methods in Climate Dynamics Plos one (2015): e67030
- David JW, Michael EF. Path Integrals in Climate Science. Plos one (2016).
- Daniel JS, Andreas WP. Path Integrals for Climate Modelling. Plos one (2019).
- Read J, Teh N. The Philosophy and Physics of Noether's Theorems: A Centenary Volume. Cambridge: Cambridge University Press (2022).
- Pham DT, Musielak ZE. Lagrangian Formalism in Biology: Standard Lagrangians and their role in Population Dynamics (2022)
- Nucci MC, Tamizhmani KM. Lagrangians for biological models (2011).
- IPCC 6th Report 2018 www.ipcc.ch/sr15
- Global Warming of 1.5 ºC- IPCC National Oceanic and Atmospheric Administration (NOAA), US Department of Commerce. Climate and Atmospheric Science's, online journal. Synthesis report of the IPCC sixth assessment report (ar6).
- Arnell NW, Lowe JA, Challinor AJ, et al. Global and regional impacts of climate change at different levels of global temperature increase climatic change 155 (2019): 377-391.
- EPA's Climate Change Indicators: Heat Waves report. The European Environment Agency (EEA)
- Thompson JN. Four central points about coevolution. Evo Edu Outreach 3 (2010): 7-13.


 Impact Factor: * 3.6
Impact Factor: * 3.6 Acceptance Rate: 76.49%
Acceptance Rate: 76.49%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 