Antibiotic Treatment, Duration of Infectiousness, and Disease Transmission
Thomas Caraco*
Department of Biological Sciences, University at Albany, Albany, NY, 12222, USA
*Corresponding Author: Thomas Caraco, Department of Biological Sciences, University at Albany, Albany, NY, 12222, USA
Received: 12 March 2021; Accepted: 22 March 2021; Published: 08 April 2021
Article Information
Citation: Thomas Caraco. Antibiotic Treatment, Duration of Infectiousness, and Disease Transmission. Journal of Environmental Science and Public Health 5 (2021): 251-272.
View / Download Pdf Share at FacebookAbstract
By curing infectious individuals, antibiotic therapy must sometimes limit the spread of contagious disease among hosts. But suppose that a diseased host stops transmitting infection due either to antibiotic cure or to non-therapeutic removal (e.g., isolation or mortality). An antibiotic`s suppression of within-host pathogen growth increases the likelihood of curing a single infection and may also reduce the probability of non-therapeutic removal. If antibiotic treatment relaxes the total rate of infection removal sufficiently to extend the average duration of infectiousness, between-host transmission can increase. That is, under some conditions, curing individuals with antibiotics can impact public health negatively (more new infections). To explore this counter-intuitive, but plausible effect, this paper assumes that a deterministic within-host dynamics drives the infectious host's time-dependent probability of pathogen transmission, as well as the probabilistic duration of the infectious period. At the within-host scale, the model varies (1) inoculum size, (2) bacterial self-regulation, (3) the time between infection and initiation of therapy, and (4) antibiotic efficacy. At the between-host scale the model varies (5) the size of groups randomly encountered in the infectious host’s environment. Results identify conditions where an antibiotic can increase duration of a host`s infectiousness, and consequently increase the expected number of new infections. At lower antibiotic efficacy, therapy might convert a rare, serious bacterial disease into a common, but treatable infection.
Keywords
Group size; Infectious contacts; Inoculum; Isolation; Pathogen extinction; Within-host dynamics
Group size articles; Infectious contacts articles; Inoculum articles; Isolation articles; Pathogen extinction articles; Within-host dynamicsarticles
Group size articles Group size Research articles Group size review articles Group size PubMed articles Group size PubMed Central articles Group size 2023 articles Group size 2024 articles Group size Scopus articles Group size impact factor journals Group size Scopus journals Group size PubMed journals Group size medical journals Group size free journals Group size best journals Group size top journals Group size free medical journals Group size famous journals Group size Google Scholar indexed journals Infectious contacts articles Infectious contacts Research articles Infectious contacts review articles Infectious contacts PubMed articles Infectious contacts PubMed Central articles Infectious contacts 2023 articles Infectious contacts 2024 articles Infectious contacts Scopus articles Infectious contacts impact factor journals Infectious contacts Scopus journals Infectious contacts PubMed journals Infectious contacts medical journals Infectious contacts free journals Infectious contacts best journals Infectious contacts top journals Infectious contacts free medical journals Infectious contacts famous journals Infectious contacts Google Scholar indexed journals Inoculum articles Inoculum Research articles Inoculum review articles Inoculum PubMed articles Inoculum PubMed Central articles Inoculum 2023 articles Inoculum 2024 articles Inoculum Scopus articles Inoculum impact factor journals Inoculum Scopus journals Inoculum PubMed journals Inoculum medical journals Inoculum free journals Inoculum best journals Inoculum top journals Inoculum free medical journals Inoculum famous journals Inoculum Google Scholar indexed journals Isolation articles Isolation Research articles Isolation review articles Isolation PubMed articles Isolation PubMed Central articles Isolation 2023 articles Isolation 2024 articles Isolation Scopus articles Isolation impact factor journals Isolation Scopus journals Isolation PubMed journals Isolation medical journals Isolation free journals Isolation best journals Isolation top journals Isolation free medical journals Isolation famous journals Isolation Google Scholar indexed journals Pathogen extinction articles Pathogen extinction Research articles Pathogen extinction review articles Pathogen extinction PubMed articles Pathogen extinction PubMed Central articles Pathogen extinction 2023 articles Pathogen extinction 2024 articles Pathogen extinction Scopus articles Pathogen extinction impact factor journals Pathogen extinction Scopus journals Pathogen extinction PubMed journals Pathogen extinction medical journals Pathogen extinction free journals Pathogen extinction best journals Pathogen extinction top journals Pathogen extinction free medical journals Pathogen extinction famous journals Pathogen extinction Google Scholar indexed journals Within-host dynamics articles Within-host dynamics Research articles Within-host dynamics review articles Within-host dynamics PubMed articles Within-host dynamics PubMed Central articles Within-host dynamics 2023 articles Within-host dynamics 2024 articles Within-host dynamics Scopus articles Within-host dynamics impact factor journals Within-host dynamics Scopus journals Within-host dynamics PubMed journals Within-host dynamics medical journals Within-host dynamics free journals Within-host dynamics best journals Within-host dynamics top journals Within-host dynamics free medical journals Within-host dynamics famous journals Within-host dynamics Google Scholar indexed journals Antibiotics articles Antibiotics Research articles Antibiotics review articles Antibiotics PubMed articles Antibiotics PubMed Central articles Antibiotics 2023 articles Antibiotics 2024 articles Antibiotics Scopus articles Antibiotics impact factor journals Antibiotics Scopus journals Antibiotics PubMed journals Antibiotics medical journals Antibiotics free journals Antibiotics best journals Antibiotics top journals Antibiotics free medical journals Antibiotics famous journals Antibiotics Google Scholar indexed journals toxicity articles toxicity Research articles toxicity review articles toxicity PubMed articles toxicity PubMed Central articles toxicity 2023 articles toxicity 2024 articles toxicity Scopus articles toxicity impact factor journals toxicity Scopus journals toxicity PubMed journals toxicity medical journals toxicity free journals toxicity best journals toxicity top journals toxicity free medical journals toxicity famous journals toxicity Google Scholar indexed journals agricultural articles agricultural Research articles agricultural review articles agricultural PubMed articles agricultural PubMed Central articles agricultural 2023 articles agricultural 2024 articles agricultural Scopus articles agricultural impact factor journals agricultural Scopus journals agricultural PubMed journals agricultural medical journals agricultural free journals agricultural best journals agricultural top journals agricultural free medical journals agricultural famous journals agricultural Google Scholar indexed journals bacteria articles bacteria Research articles bacteria review articles bacteria PubMed articles bacteria PubMed Central articles bacteria 2023 articles bacteria 2024 articles bacteria Scopus articles bacteria impact factor journals bacteria Scopus journals bacteria PubMed journals bacteria medical journals bacteria free journals bacteria best journals bacteria top journals bacteria free medical journals bacteria famous journals bacteria Google Scholar indexed journals
Article Details
1. Introduction
Antibiotics are administered routinely to humans, agricultural/pet animals, and certain plants [1-3]. Most commonly, antibiotic treatment is intended to control an individual`s bacterial infection [4]. Beyond concerns about the evolution of resistance [5, 6], use of antibiotics to treat infection presents challenging questions, including optimizing trade-offs between antibacterial efficacy and toxicity to the treated host [7]. This study asks if antibiotic treatment of an infection can have untoward consequences at the population scale; the paper models an antibiotic's direct impact on within-host pathogen dynamics and resulting, indirect effects on between-host transmission [8, 9].
The model assumes that the antibiotic`s suppression of within-host bacterial density extends the average waiting time for the host`s removal from infectiousness via other processes (e.g., physical isolation or disease mortality). The paper`s focal question asks how varying the age of infection when antibiotic treatment begins impacts both the duration of disease and the intensity of transmission during the host`s infectious period. When removal equates with disease mortality, the results identify conditions under which an antibiotic may simultaneously increase both survival of an infected individual and the expected number of secondary infections.
1.1 The infectious period
Efficacious antibiotics, by definition, reduce within-host pathogen density [10]; for some infections, antibiotics increase host survival. Therapeutic recovery of a treated individual may imply a public-health benefit. If antibiotics shorten the infectious period, the count of infections per infection could decline [4]. This interpretation follows from SIR compartment models, where neither the host-removal rate nor the antibiotically-induced recovery rate depends explicitly on within-host pathogen density. That is, antibiotics are assumed to reduce duration of the infectious period and to exert no effect on per-individual transmission intensity. By extension, antibiotics may then reduce pathogen transmission.
However, antibiotic therapy might, in other cases, increase the expected length of the infectious period. Transitions in host status must often depend on a within-host dynamics [8, 11]. As infection progresses, the pathogen density's trajectory should drive change in the rate of host removal while ill (e.g., isolation), the rate of recovery from disease, as well as the rate at which infection is transmitted [12, 13]. For many human bacterial infections, an individual can still transmit the pathogen after beginning antibiotic therapy [14]. Common infections remain transmissible for a few days to two weeks [15]. Although not addressed here, sexually transmitted disease may persist within a host for months after antibiotic therapy has begun [16]. Therapeutic reduction in pathogen density might eventually cure the host, while allowing the host to avoid isolation, etc. during treatment [17]. The result might be a longer period of infectious contacts and, consequently, increased secondary infections.
This paper assumes that with or without antibiotic treatment, a diseased host`s infectious period may be ended by a removal process that depends on within-host pathogen density. As a convenience, removal includes any event terminating infectious contacts with susceptible hosts, prior to the antibiotic curing the disease. Social/physical isolation [18] and host mortality are dynamically equivalent removals in that they end the infectious period. The model assumes that an antibiotic, by deterring within-host pathogen growth, increases the expected waiting time for removal, but an increase in antibiotic efficacy reduces the time elapsing until the host is cured. This interaction affects the count of secondary infections; disease reproduction numbers (before and after therapy begins) identify conditions where an antibiotic increases the spread of disease.
1.2 Random encounters: susceptible groups
When infection is rare, random variation in the number of contacts between diseased and susceptible hosts influences whether the pathogen does or does not spread at the population scale [19, 20]. Therefore, this paper treats reproduction numbers, i.e., infections per infection, as random variables [21]. The environment governs social group size, which can affect contacts between infectious and susceptible hosts, and so impact infection transmission [22-24]. The model asks how the number of hosts per encounter with an infectious individual (with the product of encounter rate and group size fixed) impacts the variance in the count of secondary infections; specifically, the paper asks how group size impacts the probability that a rare infection fails to invade a host population [25, 26].
1.3 Organization
The model treats within-host pathogen dynamics deterministically [2]. Removal from the infectious state and between-host transmission are modeled probabilistically [27-29]. At the within-host scale, the model considers both density-independent and self-regulated pathogen growth. The host`s removal rate and the infection-transmission intensity will depend directly on the time-dependent bacterial density. Pathogen density increases monotonically from time of infection until antibiotic treatment begins, given persistence of the host`s infectious state. The antibiotic then reduces pathogen density until the host is cured or removed prior to completing therapy (whichever occurs first).
Counts of secondary infections will require the temporal distribution of infectious contacts, since the transmission probability depends on the time-dependent pathogen density [13, 30]. The results explore effects of antibiotics and inoculum size [31] on length of the infectious period, disease reproduction numbers, and pathogen extinction. The last two results connect logically; the first addresses mean infections per infection, and the second concerns the variance in the count of new infections.
2. Within-Host Dynamics: Timing of Antibiotic Treatment
For many bacterial infections of vertebrates, little is known about within-host pathogen growth [32]. In the laboratory, Pseudomonas aeruginosa readily infects Drosophila melanogaster [33]; the pathogen increases exponentially until the host dies or antibacterial treatment begins [29, 34, 35]. In more complex host-pathogen systems, resource limitation or physical crowding must often decelerate pathogen growth within the host, implying self-regulation [36-39]. Numerical results below compare ways in which the strength of self-regulation interacts with an antibiotic to influence duration of infectiousness, and intensity of pathogen transmission.
Btrepresents the within-host bacterial density at time t; Bois the inoculum size. Antibiotic treatment begins at time tA>0. Table 1 defines symbols used in this paper.
If the pathogen grows exponentially prior to treatment, Bt= Boertfor ≤tA. The intrinsic growth rate is the difference between bacterial replication and mortality rates per unit density. The latter rate may reflect a nonspecific host immune response [40]; the model does not include explicit immune dynamics, to focus on effects of antibiotic timing and efficacy. Under logistic self-regulation, the per-unit growth rate becomes (r-cBt)where c represents intra-specific competition. For this case, the within-host density prior to treatment becomes:
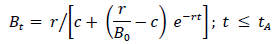
Table 1: Definitions of model symbols, organized by scale.
where Bo < r/c; the inoculum should be smaller than the ``carrying capacity.'' For the same (Bor), the self-regulated density, of course, never exceeds the exponentially growing density between time of infection and initiation of antibiotic therapy. For both growth assumptions, BtArepresents the within-host density at initiation of therapy.
Most antibiotics increase bacterial mortality [10, 41], though some impede replication [37]. When a bacterial population is treated with an efficacious antibiotic, bacterial density (at least initially) declines exponentially [42-44]. Hence, I assume that a bactericidal antibiotic induces exponential decay of Bt.
2.1 Host states
The host becomes infectious at time t=0 and remains infectious until either removed or cured by the antibiotic (see Section 2.3). No secondary infections occur after removal or therapeutic cure, whichever occurs first. Hence, transmission can occur during antibiotic therapy, prior to cure. If the host remains infectious at time t, both the probability of disease transmission (given encounter with a susceptible) and the removal rate depend explicitly on within-host density Bt.
2.2 Antibiotic concentration and efficacy
Assumptions concerning antibiotic efficacy follow Austin et al. [37]. Given that the host remains infectious at t > tA the total loss rate per unit bacterial density is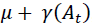 , where At is plasma concentration of antibiotic, and γ maps At to bacterial mortality per unit density.
, where At is plasma concentration of antibiotic, and γ maps At to bacterial mortality per unit density.
Assume that the antibiotic is `dripped' at rate DA. Plasma antibiotic concentration decays through both metabolism and excretion; let KA represent the total decay rate. Then,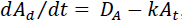 , so that ,
, so that , 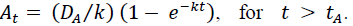 Antibiotic concentration generally approaches equilibrium faster than the dynamics of bacterial growth or decline [37]. Then a quasi-steady state assumption implies the equilibrium plasma concentration of the antibiotic is
Antibiotic concentration generally approaches equilibrium faster than the dynamics of bacterial growth or decline [37]. Then a quasi-steady state assumption implies the equilibrium plasma concentration of the antibiotic is 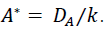 .
.
Bacterial mortality increases in a decelerating manner as antibiotic concentration increases [41, 45]. Using a standard formulation [7]:
 .
.
2.3 Antibiotic treatment duration
Antibiotic therapy begins at time . During treatment, within-host pathogen density declines as 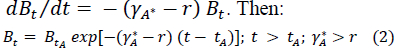
 occurs at a within-host density less than (no greater than) the density where the host may first transmit the pathogen. For exponential pathogen growth, we have:
occurs at a within-host density less than (no greater than) the density where the host may first transmit the pathogen. For exponential pathogen growth, we have:
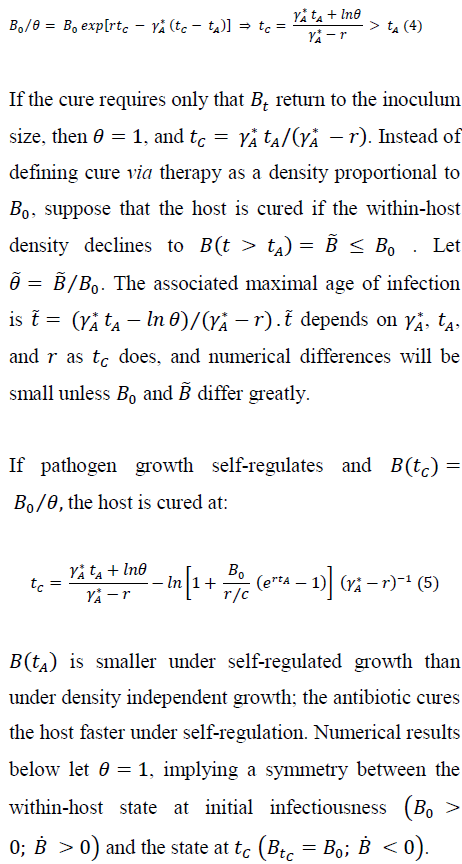
3. Duration of Infectious State
Removal includes any event, other than antibiotic cure, that ends the host's infectious period. Removal occurs probabilistically and the rate of removal depends on pathogen density. Noting that removal by mortality becomes more likely with the severity of ``pathogen burden'' [46], the model assumes that the removal rate at any time t strictly increases with pathogen density Bt.

L(t = 0)and persistence of infection declines as t increases. For logistic pathogen growth prior to treatment, we have:

3.1 Antibiotic therapy: removal vs cure
During antibiotic treatment, a host has instantaneous removal rate:

Using Eq (2), we have the probability that infectiousness persists to time during therapy, for either presence or absence of self-regulation prior to therapy:

The model's simple within-host dynamics allows the rate of removal and (its complement) persistence of the infectious state to depend clearly and explicitly on within-host pathogen density. The dynamics of infection transmission, and so any public-health implications, will also depend on within-host pathogen density [49].
4. Transmission

4.1 New-infection probabilities: before and during treatment




5. Numerical Results


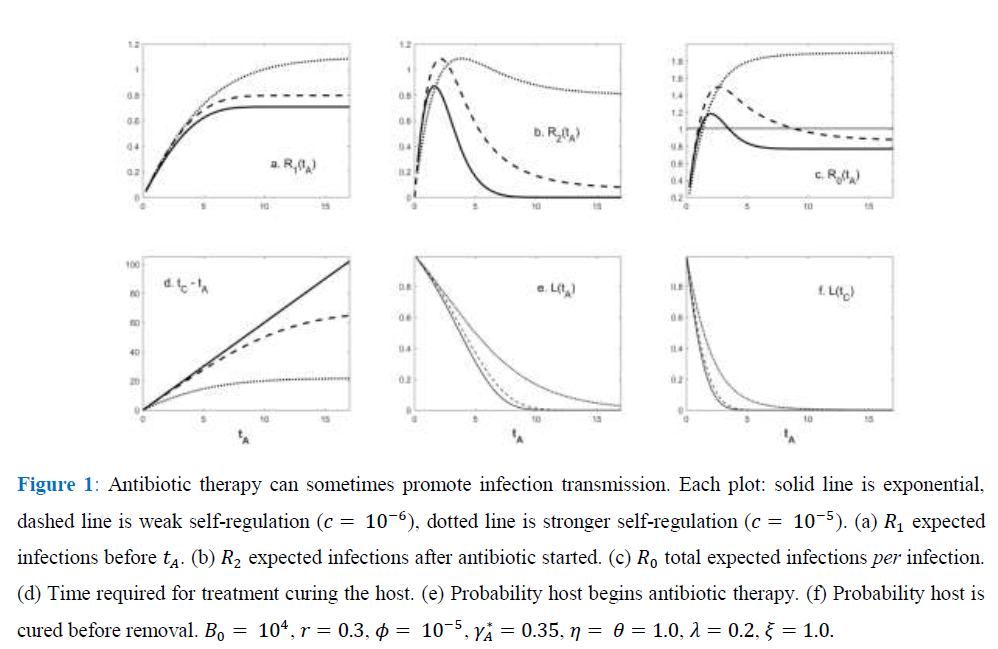

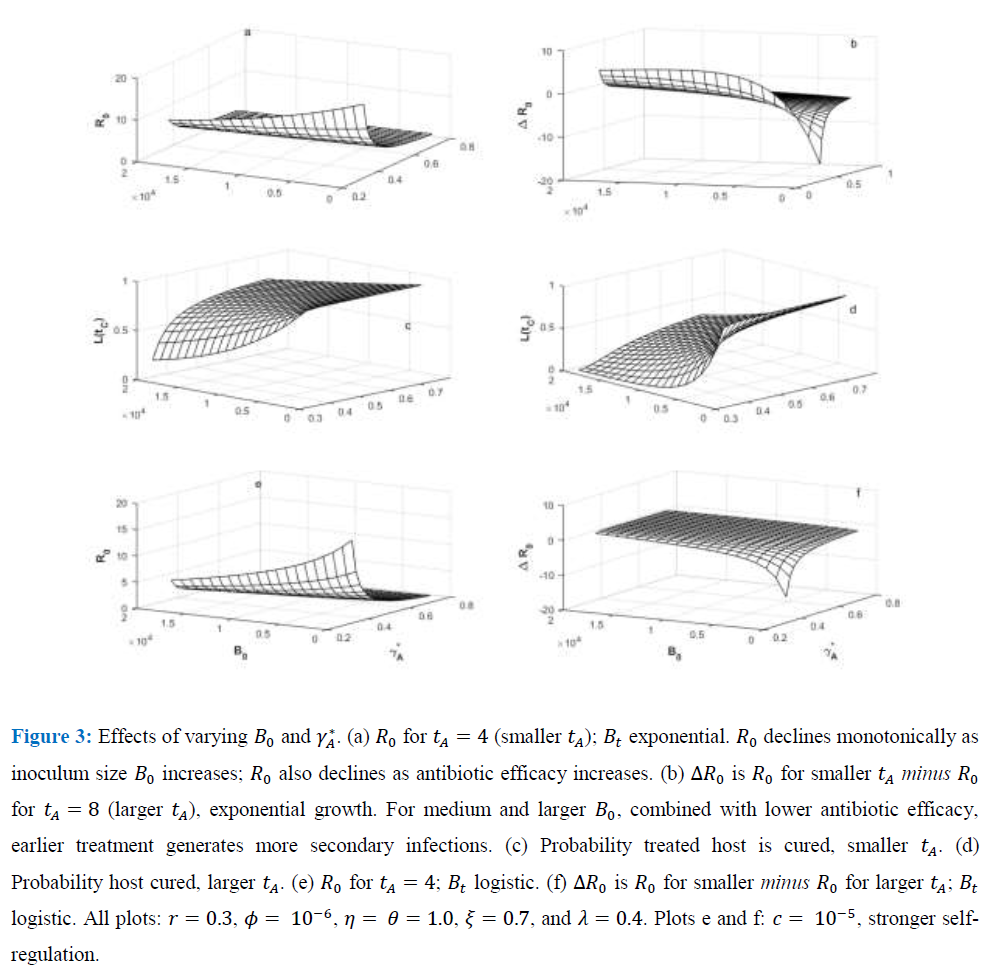
Consider the exponential case and suppose that avoiding removal through the antibiotic treatment implies surviving disease; the host is either removed by mortality or cured by the antibiotic. Then, the infected host obviously benefits from therapy. But there can be a cost at the among-host scale as the infection spreads. A rare (Ro < 1), but virulent infection in the absence of antibiotics can become a common (Ro > 1), through treatable disease when antibiotic therapy begins soon after initial infection.
Figure 2 verifies how increasing susceptible-host group size increases the probability of no secondary infections, despite independence of Ro and group size. Larger groups increase the variance in the total count of infections per infection.
As a result, the probability of no new infections (pathogen ``extinction'') increases strongly with G. Even for the tA levels maximizing Ro in Figure 1, sufficiently large group size (under both exponential and weakly self-regulated growth) assures that pathogen extinction is more likely than is spread of infection.
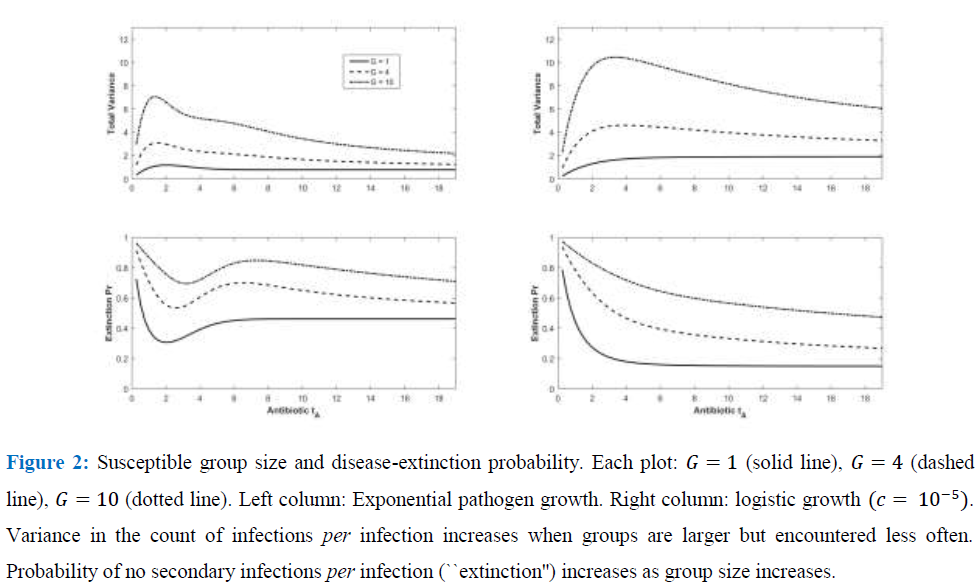
5.1 Inoculum size, antibiotic efficacy, and


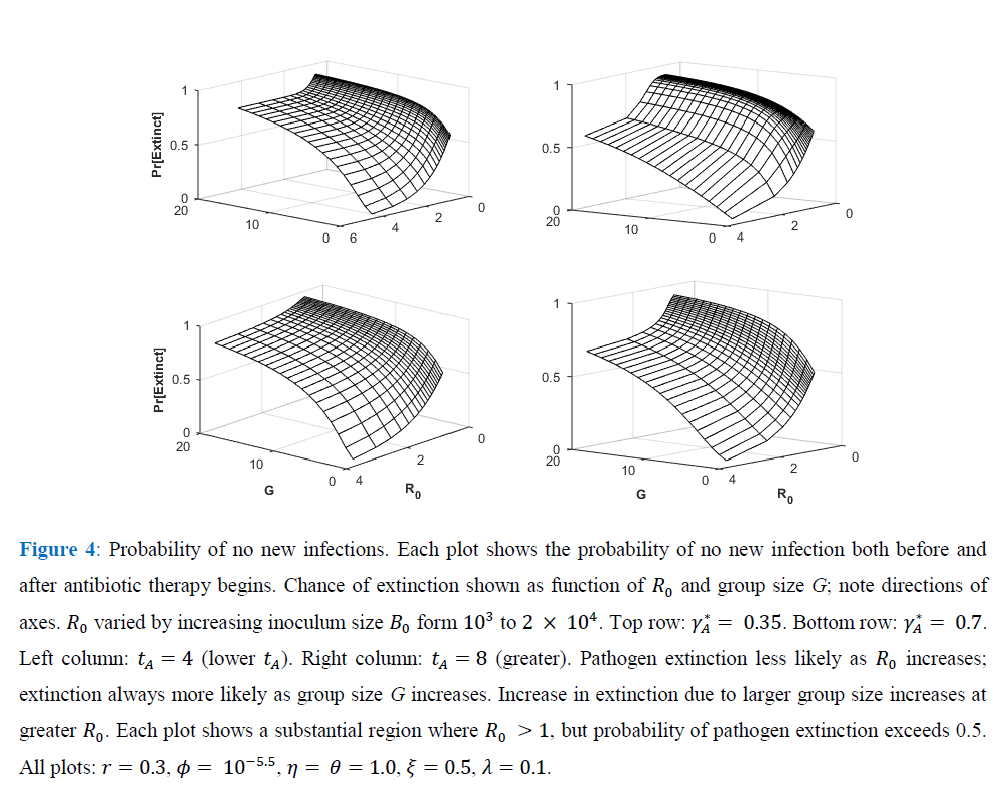
5.2 Group size, and pathogen `extinction'
Figure 4 shows, for exponential pathogen growth, how varying Ro and susceptible-group size G affects the probability that the focal host transmits no secondary infections. Ro was varied by varying Bo. Given G, pathogen-extinction probability never increases, and sometimes declines, as Ro increases. The decline is greatest when susceptible hosts are encountered as solitaries, i.e., when the infection-number variance is minimal. Given Ro, the chance of pathogen extinction increases strictly monotonically as G increases. Each plot in Figure 4 includes regions where, for sufficiently large group size, Ro > 1 but pathogen extinction is more likely than not.
6. Discussion
This paper assumes that any increase in within-host pathogen density makes removal/mortality due to infection more probable. Antibiotic therapy reduces pathogen density and so lowers the instantaneous removal rate. Removal and therapeutic recovery via antibiotics interact through their separate functional relationships with pathogen density, and this interaction governs both duration of infectiousness and disease-transmission probabilities during the infectious period. Model results show that antibiotic therapy may sometimes benefit the individual treated while imposing costs (additional disease) at the public-health scale [60].
The model was motivated by two observations. First, adults and children routinely take antibiotics (often accompanied by fever-reducing medicine) for upper respiratory infections, and then return to work or school as soon as symptoms begin to subside. Sometimes these presentees [61] remain infectious after beginning antibiotic treatment, and they transmit the associated pathogen [15]. Removal (remaining home while infectious) would diminish transmission, though at some inconvenience to the focal infective. A survey conducted within the last decade suggests that each week nearly  employees in the U.S. go to work sick [62], fearing lost wages or loss of employment [17]. Tension between pursuit of income and measures intended to curb the spread of infectious disease has become common during pandemic [63].
employees in the U.S. go to work sick [62], fearing lost wages or loss of employment [17]. Tension between pursuit of income and measures intended to curb the spread of infectious disease has become common during pandemic [63].
The second observation concerns self-medication in chimpanzees (Pan troglodytes). Chimpanzees consume a diverse plant diet, and at times select plants with antiparasitic properties [64]. When infested by intestinal nematodes, a chimpanzee will withdraw from its social group, and while isolated will eat plants with chemical and/or physical characteristics that usually reduce its parasite load [18, 65]. As symptoms moderate, the still-parasitized individual can return to the group [66] where its presence may promote transmission of the parasite. Plausibly, self-medication increases survival of the first chimpanzee, and indirectly increases the parasitism within the group. The next several subsections suggest a few questions about the way antibiotics may impact linkage between within-host pathogen growth and among-host transmission.
6.1 Bacteria
Genetic resistance to antibiotics, whether arising de novo or acquired via plasmids, challenges control of bacterial disease [4, 6, 67, 68]. Phenotypic tolerance presents related, intriguing questions [44]. Some genetically homogeneous bacterial populations consist of two phenotypes; one grows faster and exhibits antibiotic sensitivity, while the other grows more slowly and can persist after exposure to an antibiotic [43]. Phenotypes are not fixed; individual lineages may transition between the two forms [39]. An antibiotic's effect on densities of the two forms might easily extend the duration of infectiousness, but the probability of transmission, given contact, might decline as the frequency of the persistent type increases.
6.2 Antibiotic administration
If an antibiotic is delivered periodically as a pulse, rather than dripped, the therapeutically induced mortality of the pathogen can depend on time since the previous administration [44]. Complexity of the impact on the within-host dynamics could then depend on the difference between the antibiotic's decay rate and the pathogen's rate of decline. Some authors refer to an ``inoculum effect,'' suggesting that antibiotic efficacy can vary inversely with bacterial density. That is, the per unit density bacterial mortality effected by a given antibiotic concentration declines as bacterial density increases [10].
This paper asks if variation in the time elapsing between initial infectiousness and the start of antibiotic therapy could affect outcomes at the individual and population scale. Hence, was treated as an independent variable [68]. Extending the model could treat the time therapy begins as a positive random variable. Since depends nonlinearly on , randomization of the delay to treatment should produce new qualitative predictions. In some applications might be a symptom-driven function of within-host density [7, 39]. Faster within-host growth, given inoculum size, would presumably induce earlier treatment. In this case, the presence/absence of pathogen self-regulation might prove important at both the within-host and between-host scales [60].
6.3 Infected host
This paper neglects immune responses so that the duration of treatment, given cure by the antibiotic, depends explicitly on the antibiotic's efficacy and the age of infection when treatment begins. Incorporating both a constitutive and inducible immune response should be straightforward. The constitutive response imposes a constant, density-independent mortality rate on the pathogen. This response (common to vertebrates and invertebrates) is innately fixed; its effect can be inferred by varying this paper's pathogen growth rate r. Induced immune responses impose density-dependent regulation of pathogen growth; pathogen and induced densities are sometimes coupled as a resource-consumer interaction [40].
The timing of antibiotic therapy might be modulated so that the current infection might be eliminated just slowly enough to prompt a lasting immunological memory, a ‘vaccination’ against future exposure to the same pathogen [69]. Antibiotic dosing might be optimized similarly [68].
6.4 Transmission
This paper assumes a constant (probabilistic) rate of infectious contact with susceptible hosts. The number of contacts available may be limited, so that each transmission event depletes the local-susceptible pool. Regular networks capture this effect for spatially detailed transmission [54], and networks with a random number of links per host do the same when social preferences drive transmission [20]. For these cases, contact structure of the susceptible population can affect both and the likelihood of pathogen extinction when rare [28].
Contact avoidance may sometimes be more important than contact depletion [12]. If susceptible hosts recognize correlates of infectiousness, they can avoid individuals or locations where transmission is likely [70]. If antibiotics extend the period of infectiousness and reduce symptom severity, correlates of infectiousness might be more difficult to detect.
7. Conclusion
The results indicate several interrelated predictions, summarized here.
- The expected count of secondary infections is often a single-peaked function of the time since infection when therapy begins. But sufficiently strong pathogen self-regulation can imply that increases montonically with time elapsing until therapy begins.
- Less efficacious antibiotics may increase the expected count of secondary infections beyond the level anticipated without antibiotic intervention.
- Strong pathogen self-regulation increases the probability that the host remains infectious until therapeutically cured, and decreases the time elapsing between initiation of treatment and cure.
- Treatment with a less efficacious antibiotic soon after infection can increase the probability of curing the disease, but also can increase the expected count of secondary infections. However, early treatment with a strong antibiotic can both increase the likelihood of curing the disease and reduce the count of secondary infections. Antibiotics may almost always benefit the individual treated, but the consequence for public health may not be so uniform.
- If hosts are moderately to highly susceptible to infection, duration of the infectious state and the expected count of secondary infections decline as inoculum size increases.
- When susceptible hosts are grouped, and larger groups are encountered less frequently, the social structuring increases the variance of the secondary infection count and, consequently, increases the probability of no new infection.
Note that the predictions do not depend on whether removal equates with isolation (usually faster) or host mortality (usually slower).
Acknowledgements
Thanks to I-N Wang for both discussing bacteria-antibiotic interactions. Several readers offered careful, insightful comments on the model’s assumptions.
References
- McManus PS, Stockwell VO, Sundin GW, et al. Antibiotic use in plant agriculture. Annual Review of Phytopathology 40 (2002): 443-465.
- D`Agata EMC, Dupont-Rouzeyrol M, Magal P, et al. The impact of different antibiotic regimens on the emergence of antimicrobial-resistant bacteria. PLoS ONE 3 (2008): e4036.
- Gualerzi CO, Brandt L, Fabbretti A, et al. Antibiotics: targets, mechanisms, and resistance. Weinhein, Germany: Wiley-VCH Verlag (2013).
- Levin BR, Baquero F, Johnsen PJ. A model-guided analysis and perspective on the evolution and epidemiology of antibiotic resistance and its future. Current Opinions in Microbiology 19 (2014): 83-89.
- Read AF, Day T, Huijben S. The evolution of drug resistance and the curious orthodoxy of aggressive chemotherapy. Proceedings National Academy of Science USA 108 (2011): 10871-10877.
- Lopatkin AJ, Meredith HR, Srimani JK, et al. Persistence and reversal of plasmid-mediated antibiotic resistance. Nature Communications 8 (2017): 1689-1699.
- Geli P, Laxminarayan R, Dunne M, et al. One-size-fits-all? optimizing treatment duration for bacterial infections. PLoS ONE 1 (2012): e29838.
- Mideo N, Alizon S, Day T. Linking within- and between-host dynamics in the evolutionary epidemiology of infectious diseases. Trends in Ecology and Evolution 23 (2008): 511-517.
- Childs LM, El Moustaid F, Gajewski Z, et al. Linked within-host and between-host models and data for infectious diseases: a systematic review. Peer Journal 7 (2019): e7057.
- Levin BR, Udekwu KI. Population dynamics of antibiotic treatment: a mathematical model and hypotheses for time-kill and continuous-culture experiments. Antimicrobial Agents and Chemotherapy 54 (2010) 3414-3426.
- Gilchrist MA, Sasaki A. Modeling host-parasite coevolution: a nested approach based on mechanistic models. J of Theoretical Biology 218 (2002): 289-308.
- Reluga TC. Game theory of social distancing in response to an epidemic. PLoS Computational Biology 6 (2010): e1000793.
- VanderWaal KL, Ezenwa VO. Heterogeneity in pathogen transmission: mechanisms and methodology. Functional Ecology 30 (2016): 1607-1622.
- Moon M-S. Essential basic bacteriology in managing musculoarticuloskeletal infection: Bacterial anatomy, their behavior, host phagocytic activity, immune system, nutrition, and antibiotics. Asian Spine Journal 13 (2019): 343-356.
- Siegel JD, Rhinehart E, Jackson M, et al. Guideline for isolation precautions: preventing transmission of infectious agents in healthcare settings (2007).
- Falk L, Enger M, Jense JS. Time to eradication of Mycoplasma genitalium after antibiotic treatment in men and women. J of Antimicrobials and Chemotherapy 70 (2015): 3134-3140.
- deRigne L, Stoddard P, Quinn L. Workers without paid sick leave less likely to take time off for illness or injury compared to those with sick leave. Health Affairs 35 (2016): 520-527.
- Huffman MA, Gotoh S, Turner LA, et al. Seasonal trends in intestinal nematode infection and medicinal plant use among chimpanzees in the Mahale Mountains, Tanzania. Primates 38 (1997):111-125.
- Bailey NTJ. The elements of stochastic processes. New York: John Wiley and Sons (1964).
- van Baalen, M. Contact networks and the evolution of virulence. In: Dieckmann U, Metz JAJ, Sabelis MW, et al. Adaptive dynamics of infectious diseases: in pursuit of virulence management. Cambridge, UK: Cambridge University Press (2002): 85-103.
- Antia R, Regoes RR, Koella JC, et al. The role of evolution in the emergence of infectious diseases. Nature 426 (2003): 658-661.
- Brown CR, Komar N, Quick SB, et al. Arbovirus infection increases with group size. Proceedings Royal Society of London, Series B 268 (2001): 1833-1849.
- Turner J, Bowers RG, Clancy O, et al. A network model of coli O157 transmission within a typical UK dairy herd: the effect of heterogeneity and clustering on the prevalence of infection. J of Theoretical Biology 254 (2008): 45-54.
- Caraco T, Cizauskas CA, Wang I-N. Environmentally transmitted parasites: Host-jumping in a heterogeneous environment. J of Theoretical Biology 42 (2016): 33-42.
- Caraco T, Yousefi A, Wang I-N. Host-jumping, demographic stochasticity and extinction: lytic viruses. Evolutionary Ecology Research 16 (2014): 551-568.
- Lahodny G, Gautam R, Ivanek R. Estimating the probability of an extinction event or major outbreak for an environmentally transmitted infectious disease. J of Biological Dynamics (S1) 9 (2015): 128-155.
- Whittle P. The outcome of a stochastic epidemic: a note on Bailey`s paper. Biometrika 42 (1955): 116-122.
- Caillaud D, Craft ME, Meyers LA. Epidemiological effects of group size variation in social species. J of the Royal Society Interface 10 (2013): 20130206.
- Lindberg HM, McKean KA, Caraco T, et al. Within-host dynamics and random duration of pathogen infection: implications for between-host transmission. J of Theoretical Biology 446 (2018): 137-148.
- Strachan NJC, Doyle MP, Kasuga F, et al. Dose response modelling of Escherichia coli O157 incorporating data from foodborne and environmental outbreaks. International Journal of Food Microbiology 103 (2005): 35-47.
- Steinmeyer SH, Wilke CO, Pepin KM. Methods of modelling viral disease dynamics across the within- and between-host scales: the impact of viral dose on host population immunity. Philosophical Transactions Royal Society Series B 65 (2010): 1931-1941.
- Haugen MS, Hertz FB, Charbon G, et al. Growth rate of Escherichia coli during human urinary tract infection: implications for antibiotic effect. Antibiotics 8 (2019): 92.
- Mulcahy H, Sibley CD, Surette MG, et al. Drosophila melanogaster as an animal model for the study of Pseudomonas aeruginosa biofilm infections in vivo. PLoS Pathogens 7 (2011): e1002299.
- D`Argenio DA, Gallagher LS, Berg CA, et al. Drosophila as a model host for Pseudomonas aeruginosa J of Bacteriology 183 (2001): 1466-1471.
- Heo Y-J, Lee Y-R, Jung H-H, et al. Antibacterial efficacy of phages against Pseudomonas aeruginosa infections in mice and Drosophila melanogaster. Antimicrobial Agents and Chemotherapy 53 (2009): 2469-2474.
- Ebert D, Weiser WW. Optimal killing for obligate killers: the evolution of life histories and virulence of semelparous parasites. Proceedings Royal Society Series B 264 (1997): 985-991.
- Austin DJ, White NJ, Anderson RM. The dynamics of drug action on the within-host population growth of infectious agents: melding pharmacokinetics with pathogen population dynamics. J of Theoretical Biology 194 (1998): 313-339.
- O`Loughlin CT, Miller LC, Siryaporn A, et al. A quorum-sensing blocks Pseudomonas aeruginosa virulence and biofilm formation. Proceedings National Academy of Science USA 110 (2013): 17981-17986.
- Ankomah P, Levin BR. Exploring the collaboration: antibiotics and the immune response in the treatment of acute, self-limiting infections. Proceedings National Academy of Science USA 111 (2014): 8331-8338.
- Pilyugin SS, Antia R. Modeling immune responses with handling time. Bulletin of Mathematical Biology 62 (2000): 869-890.
- Regoes RR, Wiuff C, Zappala RM, et al. Pharmacodynamic functions: a multiparameter approach to the design of antibiotic treatment regimens. Antimicrobial Agents and Chemotherapy 48 (2004): 3670-3676.
- Tuomanen E, Cozens R, Tosch W, et al. The rate of killing of Escherichia coli by b-lactam antibiotics is strictly proportional to the rate of bacterial growth. J of General Microbiology 132 (1986): 1297-1304.
- Balaban NQ, Marrin J, Chalt R, et al. Bacterial persistence as a phenotypic switch. Science 305 (2004): 1622-1625.
- Wiuff C, Zappala RM, Regoes RR, et al. Phenotypic tolerance: antibiotic enrichment of noninherited resistance in bacterial populations. Antimicrobial Agents and Chemotherapy 49 (2005): 1483-1494.
- Mueller M, de la Peña A, Derendorf H. Issues in pharmacokinetics and pharmacodynamics of anti-infective agents: kill curves versus MIC. Antimicrobial Agents and Chemotherapy 48 (2004): 369-377.
- Medzhitov R, Schneider DS, Soares MP. Disease tolerance as a defense strategy. Science 335 (2012): 936-941.
- Bury KV. Statistical models in applied science. New York: John Wiley and Sons (1975).
- Missov TI, Lenart A. Gompertz-Makeham life expectancies: expressions and applications. Theoretical Population Biology 90 (2013): 29-35.
- Ganusov VV, Antia R. Trade-offs and the evolution of virulence of microparasites: do details matter? Theoretical Population Biology 64 (2003): 211-220.
- Day T, Alizon S, Mideo N. Bridging scales in the evolution of infectious disease life histories: theory. Evolution 65 (2011): 3448-3461.
- Kaitala V, Roukolainen L, Holt RD, et al. Population dynamics, invasion, and biological control of environmentally growing opportunistic pathogens. In: Hurst CJ, editor. Modeling the transmission and prevention of infectious disease: advances in environmental microbiology 4. New York: Springer Intl Publications AG (2017): 213-244.
- Tenuis PFM, van der Heijden OG, van der Giessen JWB, et al. The dose-response relation in human volunteers for gastro-intestinal pathogens. Bilthoven, The Netherlands: National Institute of Public Health and the Environment (1996).
- Keeling MJ, Grenfell BT. Effect of variability in infection period on the persistence and spatial spread of infectious diseases. Mathematical Biosciences 147 (1998): 207-226.
- Caraco T, Glavanakov S, Li S, et al. Spatially structured superinfection and the evolution of disease virulence. Theoretical Population Biology 69 (2006): 367-384.
- Ross SM. Stochastic processes. New York: John Wiley and Sons (1983).
- Schmid-Hempel P, Frank SA. Pathogenesis, virulence, and infective dose. PLoS Pathogens 3 (2007): e147.
- White SM, Burden JP, Maini PK, et al. Modelling the within-host growth of viral infections in insects. J of Theoretical Biology 312 (2012): 34-43.
- Gama JA, Abby SS, Vieira-Silva S, et al. Immune subversion and quorum-sensing shape the variation in infectious dose among bacterial pathogens. PLoS Pathogens 8 (2012): e1002503.
- Chu C-M, Poon LLM, Cheng VCC, et al. Initial viral load and the outcomes of SARS. Canadian Medical Association Journal 171 (2004): 1349-1352.
- Scire J, Hozé N, Uecker H. Aggressive or moderate drug therapy for infectious diseases? Trade-offs between different treatment goals at the individual and population levels. PLoS Computational Biology 15 (2019): e1007223.
- Kivimaki M, Head J, Ferrie JE, et al. Working while ill as a risk factor for serious coronary events: the Whitehall II study. American Journal of Public Health 95 (2005): 98-102.
- Susser P, Ziebarth HR. Profiling the U.S. sick leave landscape: presenteeism among females. Health Services Res 51 (2016)0: 2305-2317.
- Maxouris C, Chavez N. Florida will be like a house on fire in weeks with loose coronavirus restrictions, infectious disease expert says. CNN Health (2020).
- Ahoua ARC, Konan AG, Bonfoh B, et al. Antimicrobial potential of 27 plants consumed by chimpanzees (Pan troglodytes verus Blumenbach) in Ivory Coast. BMC Complem Alternative Medicine 15 (2015): 383.
- Pebsworth P, Krief S, Huffman MA. The role of diet in self-medication among chimpanzees in the Sonso and Kanyawara comunities, Uganda. In: Newton-Fisher NE, Norman H, Reynolds W, Paterson JD, editors. Primates of western Uganda. New York: Springer (2006): 105-133.
- Huffman MA, Page JE, Sukhdeo MVK, et al. Leaf-swallowing by chimpanzees: a behavioral adaptation for the control of strongyle nematode infections. Inter Journal of Primatology 17 (1996): 475-503.
- Drlica K. The mutant selection window and antimicrobial resistance. J Antimicrobial Chemotherapy 52 (2003): 11-17.
- Gjini E, Brito PH. Integrating antimicrobial therapy with host immunity to fight drug-resistant infections: classical vs adaptive treatment. PLoS Computational Biology 12 (2016): e1004857.
- Stromberg SP, Antia R. Vaccination by delayed treatment of infection. Vaccine 29 (2011): 9624-9631.
- Caraco T, Turner WC. Pathogen transmission at stage-structured infectious patches: killers and vaccinators. J of Theoretical Biology 436 (2018): 51-63.


 Impact Factor: * 3.6
Impact Factor: * 3.6 Acceptance Rate: 76.49%
Acceptance Rate: 76.49%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 