Article Information

Onyenanu O. Adaobi¹, Iheanyi S. Iwueze², Emmanuel O. Biu¹, Christopher Onyema Arimie^3*

¹Department of Mathematics and Statistics, University of Port Harcourt, Rivers State

²Department of Mathematics and Statistics, Federal University of Technology Owerri, Imo State, Nigeria

³Department of Radiology, University of Port Harcourt Teaching Hospital, Rivers State, Nigeria

^*Corresponding Author: Christopher Onyema Arimie, Department of Radiology, University of Port Harcourt Teaching Hospital, Rivers State, Nigeria

Received: 09 December 2020; Accepted: 19 December 2020; Published: 16 February 2021

Citation: Onyenanu O. Adaobi, Iheanyi S. Iwueze, Emmanuel O. Biu, Christopher Onyema Arimie. On The Analysis of Blood Glucose Levels of Diabetic Patients. Fortune Journal of Health Sciences 4 (2021): 257-283.

Abstract

Keywords

Diabetic patients; Blood glucose level; Paired Observation tests; Normality test; Diabetes

Article Details

1. Introduction

Diabetes is a disease associated with high level of glucose (sugar) in the blood of the sufferer. It is very harmful to the body. Blood glucose testing involves measuring the levels of blood glucose after fasting and after glucose intake. Fasting blood sugar test is required to diagnose diabetes and Oral glucose tolerance test (OGTT), done after glucose intake, helps to monitor the glucose level in the blood of a patient. A hormone called insulin manages or regulates the glucose level in the body. When the body cannot produce enough insulin or when the insulin produced cannot work effectively owing to some other conditions, the blood sugar level rises causing diabetes. If it is too high or too low, medical attention will be needed.

Statistical tests such as Paired Observation tests (including parametric and Non-parametric tests) are useful for ascertaining if there is any significant mean difference between the two measurements (before and after administration of glucose). Also, two sample t-test is useful for checking whether the level of change in fasting blood sugar after two hours is the same with the level of change after administration of glucose. In paired observation, we have Univariate case and Multivariate cases. In Univariate case, two samples obtained are correlated and must be dependent. The two samples are reduced to one by working the differences between the paired observations. Here, the assumptions are: X and Y have a bivariate normal distribution and, X and Y are correlated [1].

The approach used in controlling diabetes is the blood glucose testing. This test measures the concentration of glucose in the blood. Blood glucose testing consist of fasting blood glucose and glucose intake measurements. The fasting blood sugar is used to diagnose diabetes while glucose intake is conducted to measure the blood glucose level. Oral glucose tolerance test (OGTT) measures first and second stage insulin response to glucose. It compares the level of glucose in the blood before and after administering glucose. After testing the blood glucose level in the patient fasting, 75grams of glucose dissolved in water is given to the patient and another test conducted at one hour and two hours’ interval. A glucometer (glucose meter) is used to measure blood glucose and the unit of measurement is mg/dl or mmol/l. Blood glucose level outside the normal range may be an indicator of a medical condition. If the blood sugar measured is greater than 140gm/dl two hours after, it means the person is pre-diabetic. If it is greater than 199mg/dl two hours after, it means the person has full blown diabetes. If the result is 139mg/dl, it is considered as normal. The purpose of testing blood glucose several times per day is to discover when the blood glucose level is going too low or too high. This will help the doctor to timely take steps to prevent the occurrence of low or high blood glucose levels. The test becomes a warning to those who fall into the category of pre-diabetic and full blown diabetes as it enables them to change their lifestyle and cut down the intake of foods that has the capacity to increase blood glucose level. It is also beneficial in the sense that it gives information on whether the body can tolerate glucose or not.

It is the practice in hospitals that when a patient arrives, the patient is kept two hours before administration of glucose thereafter, the patient is kept for another two hours to monitor glucose level [2]. The problem here is to ascertain whether the resting period of two hours is adequate or not and secondly, is the level of change after two hours for fasting glucose and the level of change two hours after glucose administration the same? The purpose of this study is to determine whether there is any significant difference between fasting blood sugar test and oral glucose tolerance test by performing a statistical analysis on blood glucose measurements obtained from the medical laboratory department of a University Teaching Hospital in Nigeria.

The specific objectives are to:

1. Determine statistically the adequate period of rest before the administration of glucose.
2. Determine whether the glucose level increased after one hour, two hours after glucose administration.
3. Determine if the level of change after two hours, for fasting glucose is the same with the level of change two hours after glucose administration.

There are many paired observation test statistics available but this research is limited to three paired observation tests (parametric Paired t-test, Non-parametric Wilcoxon ranked sign test and Sign test) only. Sign test of the median, Wilcoxon signed rank test and paired t-test, were performed to ascertain whether the level of change after one hour and two hour intervals for fasting glucose and after glucose administration, respectively was the same. The two sample t–tests was performed to check whether the level of change in blood glucose for fasting blood sugar test was the same with the test done two hours after glucose intake.

2. Review of Literature

2.1 Review of works on glucose test

Glucose, the simplest form of sugar, is the body’s major source of energy while, glucose test measures the amount of glucose in the blood. A hormone called Insulin regulates blood glucose level in the body. According to Martel (2012) [3], Diabetes occurs when the body does not produce enough insulin thereby causing the blood glucose to rise, or when the body cannot use the insulin produced effectively. If diabetes is left untreated, the high blood glucose level will cause damages in the organs. People with diabetes normally go for blood glucose test to determine whether their condition is being managed well or not. A high blood glucose level is an indication of poor management of the diabetes. Blood glucose testing provides information that helps the physician to make decisions on diet and medication dosage.

Saudek et al (2006) [4], states that since there is increasing rate of diabetes, there is need to learn how to successfully control blood glucose level as this, leads to significant reduction in mortality due to diabetes, where assessing glycaemia in diabetes is challenging.

According to Haller et al. (2004) [5], blood glucose testing helps in administration of medication e.g., deciding the dosage to take. It also tells when the blood glucose level is high or low. An important benefit of blood sugar testing is that diabetic patients are sensitized to read and interpret their results thus, enabling them to take proper actions to improve control of the disease. People on insulin therapy or other medications should test their blood glucose level regularly so as to know when their blood glucose level is going too low or too high. Fasting blood sugar test is used to diagnose diabetes while Oral glucose tolerance test is conducted to measure blood glucose level. People with diabetes always have their blood sugar level higher than those without diabetes. According to American Diabetes Association (2006) [6], the normal level of blood glucose in diagnosis ranges from 126mg/dl to 140mg/dl.

2.2 Review of works on Paired Observation Tests

Given two random samples from two populations, we call the data paired if the j^th measurement of the first sample is paired with the k^th measurement of the second sample. Paired data or observations can be analyzed using parametric and non-parametric methods.

Conover (1999) [7], states that parametric test involves population distribution that has a particular form and also involves hypothesis about the population parameters, while non-parametric test does not make assumptions about the underlying distribution. Non-parametric tests use approximate solutions to a particular problem, while parametric tests use particular solutions to approximate problems. Hollander and Wolfe (1973) [8], posits that parametric test depends on distributional assumptions while non – parametric test do not require any strict distributional assumptions. They analyze ranks of a variable instead of using the original values.

Paired t – test is a parametric statistical method used to compare two population means that emanate from two samples that are correlated. According to Zaiontz (2013) [9], paired t – test is used to test for the differences in mean of two samples which are dependent on one another. In this case, the null hypothesis is such that the mean difference is equal to zero. Paired t – test involves comparing two means for information where every person who participated in one sample also participated in the other sample. The difference scores are created for every individual, and we compare mean differences between the results with the mean difference for the population [10,11].

Non-parametric tests for analyzing paired observations include the Sign Test and the Wilcoxon Signed Rank Test. Given n observations from a population with two samples u and v. For each observation, two paired samples {u₁...u_n} and {v₁ . . . v_n} will result. In conducting Wilcoxon signed rank test for paired samples where Z_i = v_i – u_i for all i = 1 . . . n, it is required that Z_i are independent. For v_i and u_i, ranking can then be applied and differences taken. Also, the distribution of Z_i’s is symmetric. The hypothesis, H₀ can be stated as “the distribution of difference scores in the population is symmetric about zero” [9]. The Wilcoxon signed rank test is used to test if the median of a symmetric population is zero. Firstly, the data is ranked without regarding the sign. Secondly, we attach the signs of the main observation to their corresponding ranks [12]. The test can also be applied in the comparison of two dependent or correlated data in which the measurements are ordinal and for samples that are matched or measurements that are repeated on a single sample to check whether the rank in their population mean differ or not [13,14]. In this case, the null hypothesis is that there is no difference in the two paired measurements. According to Mcdonald (2014) [15], the difference scores between the two paired values are computed then, the absolute differences from the smallest to the largest are taken from the measurements. After that, ranks are assigned to the values. Signs (+ or –) are also assigned according to the differences. The sum of positive and the negative ranks respectively, are then computed. The rank of all differences in one direction should be added and the smaller of those sums becomes the test statistic. The z distribution approximation for large samples is used and the statistical decision is to reject the null hypothesis if z calculated is greater than 1.96 at 0.05 level of significance.

The Sign test is a non-parametric method used to test the differences between pairs of observations. It is used to determine whether one of a pair of observation is greater or less than the other. It can also be used to test for trend in series of ordinal measurements or a test for correlation [16]. Sign test is used to test a claim that involves matched pairs of sample data, a claim involving numerical data with two categories, or a claim about the population median against a hypothesized value. In other to use it, the data values are first converted to ‘plus’ and ‘minus’ signs before testing. The sign test makes very few assumptions about the type of distributions under test. It tests the hypothesis that the differences can either be positive or negative using paired data. The test statistic for large samples is (plus – minus)² / (plus + minus). ‘Plus’ is the number of positive values and ‘minus’ is the number of negative values. The hypothesis is “the positive and negative values are equally likely” and the test statistic follows chi square distribution with one degree of freedom [17]. Sign test is used to compare the differences between paired groups, analyzing only the signs of the difference scores. The null hypothesis is “the median difference is zero”. If the null hypothesis is true, then approximately half of the differences will be positive and the other half will be negative. The test statistic is the smaller of the number of positive signs or negative signs. The critical value is determined using the Sign Test Table. The decision is to reject H₀ if the test statistic (i.e., the smaller of the positive or negative signs) is less than or equal to the critical value. The p-value is computed based on the observed test statistic.

The sign test is different from the Wilcoxon Signed rank test as the latter is rank based and considers the magnitude of the differences between the paired samples rather than their signs. Both tests differ from parametric t test and assumes that the distribution of the differences within pairs are symmetric without needing normality [8]. In paired samples, we are interested in testing whether the population median is equal or not. That is,

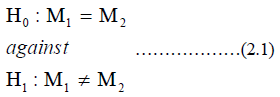
If the parametric test assumptions are satisfied, then paired sample t – test can be used to test the hypothesis.

Sign test can also be used to check if a binomial distribution has equal chance of success and failure. In this case, the differences of the paired values, using the signs of the individual differences, are taken. Then, the binomial distribution table is used for the test assuming probability, p = 0.5 when the sign is positive and q = 0.5 when the sign is negative [16]. Here, the null hypothesis is “the number of positive differences is approximately equal to the number of negative differences”. Lucky and Bright (2012) [18], noted that Sign and Wilcoxon signed rank tests are most suitable for analyzing ranked or ordinal data which often deviate drastically from normality thus, making the use of parametric test unsuitable.

The sign test and Wilcoxon signed rank test have been used to analyze many real life occurrences. Ho, et al. (2004) [19] used the Wilcoxon Signed-Rank Test to analyze the effect of a plastic implant into the soft palate of 12 chronic snorers to see if it would reduce the volume of snoring. The result showed that the median change in snoring volume was significantly different from zero. In another experiment, Buchwalder and Huber-Eicher (2004) [20] also used the Wilcoxon Signed-Rank Test to study the aggressive reactions of turkeys housed in pens towards unfamiliar turkey brought into the pen. They found that the median difference between the number of pecks per test in the small pen and in the large pen was significantly greater than zero.

3. Methods

Statistical analysis on blood glucose measurements of 47 Diabetic Patients obtained from the medical laboratory department of Nnamdi Azikiwe University Teaching Hospital, Nnewi, Anambra State, Nigeria was done using paired observation tests, and two sample t test. The Jarque-Bera (JB) test was used to test for normality of the sample data before the analysis. Definitions and methods of data analysis used are discussed in the following sub-sections. Minitab 18 statistical software was used for all the computations.

3.1 Jarque – Bera (JB) test

The JB test is based on the classical measures of skewness and kurtosis. It is a “goodness – of – fit” test used to check whether the sample data has the skewness and kurtosis matching the normal distribution. The JB statistic has a chi squared distribution with two degrees of freedom χ ² (2)[21]. The JB statistic [22] is given as:

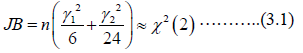
where,

γ₁ is the skewness, γ ₂ is the kurtosis and n is the sample size.

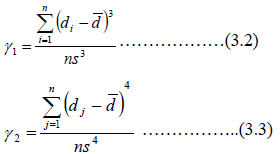
where,

d is the difference in each observation,

s is the standard deviation.

Equation (3.1) was used to test whether the differences obtain are normally distributed or not.

Hypothesis:

H₀: Data follows a standard normal distribution.

H₁: Data does not follow a standard normal distribution.

Decision rule: we reject H_0, if JB > χ ²(2), otherwise accept H₀

3.2 Paired Observations Tests

In this section, we describe parametric and non-parametric methods used in the study. The methods are Paired t test, Wilcoxon Signed Rank Test and Sign Test for paired samples.

1. Paired t – test: Paired t – test matches responses which are dependent or which are related in a pairwise manner. The matching helps to detect variability that is between the pairs which usually result in small error terms thus, increasing the sensitivity of the hypothesis test or confidence interval. It is used to determine if there are any significant differences that exist between the mean values, under two different conditions but with the same measurement.

Therefore, the paired t-test hypothesis is:

H₀: There is no significant mean difference between the two paired samples.

H₁: There is significant mean difference between the two paired samples.

That is,

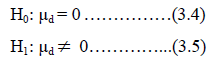
Where μ _d is estimated by the mean differences  between the fasting blood glucose test  and oral glucose tolerance test ( ); using = 0.05

The t-statistic is given as:

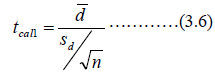
where,

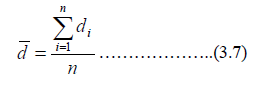
And

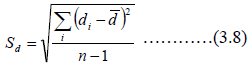
Using the confidence interval (CI),

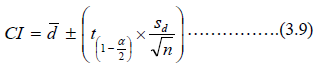
Accept , if the  confidence internal (CI) for the mean difference include zero [17,23].

Note that,

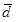= Mean difference between paired samples.

µ_d = hypothesized population mean difference (usually 0).

S_d = standard deviation of paired differences.

d_i= sample item difference.

 n = sample size (number of pairs in the sample).

 n – 1 = degree of freedom for the test statistics.

 t = paired sample t–test.

In other words, if t calculated is less than the t tabulated, we reject H₀ otherwise we accept the null hypothesis.

2. Assumptions of paired t-test

The test can only be performed with the matched pairs of sample. The differences of the paired sample must be normally distributed and the data must be continuous.

1. Wilcoxon Signed Ranked Test

Wilcoxon signed ranked test is useful in cases involving symmetric continuous distribution. In using it, we assume that the mean is equal to the median.

The null hypothesis is

Given the random samples x₁, x₂, . . . , x_n which come from a continuous and symmetric distribution with mean (median) = µ

1. Comparing the differences 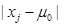where j = 1, 2, . . . , n
2. We are to rank the absolute differences 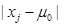for j = 1, 2 , . . , n in ascending order
3. Signs + or – are allocated based on the direction of the differences, by computing the sum of the positive and the negative ranks respectively.
4. Denoting the sum of positive ranks by r⁺ and the sum of negative ranks as r^-.

The test statistic is given as

where R is the Wilcoxon signed rank

If R calculated is less than or equal to tabulated R, we reject H₀ at 0.05 level of significance [17].

Assumptions of Wilcoxon Signed Rank test

The difference between the two data values of a pair is continuous and symmetric. The two samples need to be dependent observations of the cases and the data are measured on an ordinal or interval scale.

2. Sign test

 Sign test, as had been discussed in section 2.1, is used to compare outcomes between paired groups, where only the signs of the difference scores are analyzed. The Probability value (p-value) is computed based on the observed test statistic; the test statistic follows a binomial distribution.

We have

p (x is success) = [n!/x!(n – X)!] p^x (1 – p)^{n – x}…….(3.12)

where,

n = no of observation,

p is the probability of success or failure = 0.5.

x denotes the Sign test statistic [17].

Assumptions of Sign Test

The observation can be independent. It can be identically distributed and the measurement scale is at least ordinal.

Our interest was to determine whether the binomial distribution has equal chance of success and failure hence, we compared the outcome between fasting blood glucose test (X_i)and oral glucose tolerance test (Y_i); using α at 99%, 95% and 90% confidence level respectively.

3.3  Two sample t- test

Two sample t-test is a statistical method used to evaluate whether the means of two independent populations differ or not, the observation from one sample are not related to the observation from the other sample. The two sample t-test uses the sample standard deviations to estimate the variance, σ² for each population [24-26]. Reject the null hypothesis if the p-value is less than 0.05.

We compare the level of change in 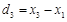which has to do with two hours before glucose intake and the level of change in 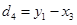after glucose administration whether they are the same or not.

The hypothesis is

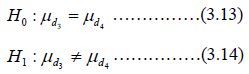
where,

d₃= change in blood sugar after two hours for fasting patients.

d₄= change in blood sugar after administration of glucose.

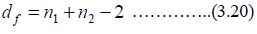
where,

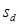= the standard deviation of the differences.

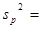the pooled sample variance from population 1 and population 2.

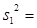variance of the sample difference one.

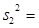variance of the sample difference two.

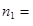size of the sample difference one.

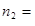size of the sample difference two.

 k is the third difference (d₃)

 l is the fourth difference (d₄)

Assumptions of two sample t- test

The data are continuous, they follow normal distribution and variances of the two populations are equal. The two samples are independent and both are simple random samples from their respective population.

3.4   Definition and measurement of variables

The fasting variables were taken on two different occasions after the initial value, X₁ at one-hour and two-hour interval each. The glucose intake variables were also taking on two occasions at one-hour interval each. Paired Observation tests were used to check whether it is possible to take the recording on three occasions. For the fasting variables we denote the variables with x₁, x₂, and x₃.

where,

X₁ = blood glucose test on arrival.

X₂ = blood glucose after resting for one hour.

X₃ =blood glucose test after two hours.

On the other hand, we denote the glucose intake variables with y₁, y₂,

where,

y₁ =blood glucose test taken one hour after administration of glucose.

y₂ =blood glucose test taken two hours after administration of glucose.

For the fasting variables, the differences are:

d₁ = x₂ – x₁ (change in blood sugar after one hour for fasting patients)

d₂ = x₃ – x₂ (change in blood sugar for fasting patents at an interval of one –two hours)

d₃ = x₃ – x₁ (change in blood sugar level after two hours for fasting patients)

For the glucose intake variables, the differences are:

d₄ = y₁ – x₃ (change in blood sugar level after one hour of administration of glucose)

d₅ = y₂ – x₃ (change in blood sugar level after two hours of glucose administration).

d₆ = y₂ – y₁ (change in blood sugar level at one-hour and two-hour interval after glucose administration).

4. Results

The aim of this work is to determine whether there is any significant difference between fasting blood sugar test and oral glucose tolerance test. The fasting blood sugar test was done hourly on two different occasions, while the oral glucose test was done hourly on two different occasions also. Paired observation tests were done to determine whether it is necessary to test diabetic patients fasting blood sugar hourly up to two different times or not and glucose intake hourly up to two different times, using paired t-test (parametric), Wilcoxon signed rank test and Sign test (Non-parametric). Finally, two sample t-test was used to test whether the level of change after two hours for fasting glucose is the same as the level of change one hour after glucose intake. The results are given in the following subsections.

4.1 Jarque-Bera (JB) test Result

This test was used to test for normality of the data set differences stated in Section 3.1, for the fasting and glucose intake variables. The results are shown in Table 1.

Table 1: Jarque-Bera (JB) test Results

From the Table 1, d₁ = 11.47 and d₆ = 259.7 are both greater than 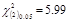while d_2, d_3, d₄ and d₅ are less than 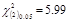. This implies that not all the data set differences are normally distributed (d₁ and d₆ are not normally distributed) thus, indicating the use of both parametric and non-parametric tests.

4.2  Paired Observations Tests Results

Since the fasting variables are taking on two different occasions, we tested whether it is necessary to take the measurement at one-hour interval before administering glucose to the patient. Tables 2 to 4 summarizes the data set differences test results using the Paired t– test, Wilcoxon signed rank test and Sign test at 99%, 95% and 90% confidence intervals, respectively.

Table 2: Blood glucose test results at 99% Confidence Interval

Remark: If p > 0.05, we accept H₀

Table 3: Blood glucose test results at 95% Confidence Interval

Remark: If p > 0.05, we accept H₀

Table 4: Blood glucose test results at 90% Confidence Interval

Remark: If p > 0.05, we accept H₀

The results (Tables 2 to 4), show that:

For paired t – test of fasting variables x₁ and x₂, the confidence interval for the mean difference between the two fasting variables include zero suggesting that there is no significant difference between them. The p–value is 0.074 further suggesting that the data are consistent with H₀: µ_d = 0. Since p > 0.05, we accept H₀ and conclude that there is no difference between the two paired samples.

For Wilcoxon signed rank test, the fasting variables, x₁ and x₂ measurement results shows that p – value (p = 0.060) is greater than 0.05 and the median difference between x₁ and x₂ is zero. Therefore, we accept H_o and conclude that there is no significant difference in median of the fasting variables after one-hour interval. However, the sign test for the fasting variables, x₁ and x₂ shows that the p – value (p = 0.0226) is less than 0.05 implying difference between them hence, we reject H₀ and conclude that the fasting variables, x₁ and x₂ do not have common median.

4.3 Two sample t- test Result

From Section 3.4, the level of change after two hours for fasting glucose, d₃ = x₃ – x₁ and the level of change one hour after glucose administration, d₄ = y₁ – x₃. We computed the means and variances of both d₃ and d₄, and their pooled variance as discussed in Section 3.3. The results show that 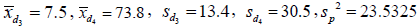, p = 0.000 and df=92 . The p-value _cal (0.000) is less than p-value _tab (0.05), we reject H₀ and conclude that there is significant difference between the level of change in blood sugar for fasting patients and the level of change in blood sugar after administration of glucose.

5. Discussion

These results suggest that it is not necessary to take the blood glucose measurements every one hour rather, it should be taken every two hours since there was no difference between blood glucose tested on arrival and one hour after resting, as shown by the results of paired t – test and Wilcoxon signed rank test at all three levels of significance (99%, 95% and 90%) respectively. This implies that conducting fasting blood glucose test three different times on a visit, is not necessary as it amounts to a waste of time, money and resources. Furthermore, d₂ to d₆ in Tables 2 to 4, have p-values (p = 0.00) less than 0.05 for all the three paired-observation tests, indicating that there is significant difference between the variables. The change in blood sugar level after glucose intake is significant. The blood sugar level increased progressively after administering glucose at one-hour and two-hour intervals. This shows that a measurement in one hour or two after administering glucose is sufficient to give the diagnosis. There was significant difference between the change in blood sugar level after two hours for fasting glucose test and after one hour of glucose administration for the Oral glucose tolerance test. As a result, it is necessary to measure glucose level at hourly intervals after administering glucose to help monitor when the blood glucose level is too high or too low.

6. Conclusion

Based on the above results, it was concluded that a single fasting blood glucose test is sufficient to diagnose diabetes on a visit to the laboratory while oral glucose tolerance test conducted hourly is necessary to monitor the blood to know when the glucose level is going high or low.

Acknowledgement

We thank the Management and staff of Chemical Pathology Laboratory of Nnamdi Azikiwe University Teaching Hospital Nnewi for providing the information/test results that formed the data used for this study.

References

1. Alvin CR: Methods of multivariate Analysis; 2nd edition USA; John Wiley and sons, Inc (2002).
2. Henry JB. Clinical diagnosis and management by laboratory methods (20th edition) Philadelphia, Saunders (2001).
3. Martel Y. Odd Diabetes Trick “Kills” Diabetes Industry (2012).
4. Saudek CD, Derr RL, Kalyani RR. Assessing glycemia in diabetes using self-monitoring blood glucose and hemoglobin A1c. JAMA 295 (2006): 1688-1697.
5. Haller MJ, Stalvey MS, Silverstein JH. Predictors of control of diabetes: monitoring may be the key. The Journal of Pediatrics 144 (2004): 660-661.
6. American Diabetes Association: “January 2006 Diabetes Care “Diabetes Care 29 (2006): 51-580.
7. Conover WJ. Practical non-parametric Statistics (3^rd edition) john Wiley and sons, Inc (1999).
8. Hollander M, Wolfe DA. Nonparametric statistical methods (1973).
9. Zaiontz C. Real statistics using Excel. Obtenido de http://www. real-statistics. Com (2015).
10. Nolan SA, Heinzen T. Step by step solutions; T- tests: paired/dependent independent; statistics for the Behavioral Sciences (2002).
11. Martin K, Naomi A. Points of Significance Comparing sample mean (2014).
12. Rosner B, Glynn RJ, Lee ML. The Wilcoxon signed rank test for paired comparisons of clustered data. Biometrics 62 (2006): 185-192.
13. Lehman EL. Nonparametrics: Statistical Methods Based on Ranks. San Francisco: Holden-Oay (1975).
14. Shier R. “statistics” The Wilcoxon signed Rank sum test, mathematics learning support Centre (2004): 1-3.
15. McDonald HJ. A Handbook of Biological Statistics 3^rd edition (2014): 186-189.
16. Nwobi FN, Nduka EC. Statistical Notes and Tables for Research; 2^nd edition, Alphabet Nigeria Publishers, Owerri (2003).
17. Corder GW, Foreman DI. Nonparametric statistics: A step-by-step approach. John Wiley & Sons (2014).
18. Ochei LS, Ajibade BF. Methodology in Non-parametric Statistics; Proceedings of Bi-annual National Conference of Statistics Research Group (2012): pp 102-110.
19. Ho WK, Wei WI, Chung KF. Managing disturbing snoring with palatal implants: a pilot study. Archives of Otolaryngology–Head & Neck Surgery 130 (2004): 753-758.
20. Buchwalder T, Huber-Eicher B. Effect of increased floor space on aggressive behaviour in male turkeys (Meleagris gallopavo). Applied Animal Behaviour Science 89 (2004): 207-214.
21. Brys G, Hubert M, Struyf A. Robust measures of tail weight. Computational Statistics & Data Analysis 50 (2006): 733-759.
22. Bera AK, Jarque CM. Efficient tests for normality, homoscedasticity and serial independence of regression residuals: Monte Carlo evidence. Economics Letters 7 (1981): 313-318.
23. Nduka EC. Statistics Concepts and Methods. 3^rd Edition Reprinted, Clara’s Prints, Port Harcourt, Nigeria (2015).
24. Hakstian AR, Roed JC, Lind JC. Two-sample T–2 procedure and the assumption of homogeneous covariance matrices. Psychological Bulletin 86 (1979): 1255.
25. Delaney HD, Vargha A. The Effect of Nonnormality on Student's Two-Sample T Test (2000).
26. Lehman A, O'Rourke N, Hatcher L, et al. JMP for basic univariate and multivariate statistics: methods for researchers and social scientists. Sas Institute (2013).
27. Dallar GE. Non parametric Statistics (2000).

Appendix A

The Data (Blood Glucose Measurements) Used For The Statistical Analysis.

Fasting blood sugar variable                                                             Glucose intake variables

Data Source: Nnamdi Azikiwe University Teaching Hospital Nnewi (NAUTH), 2019.

Appendix B

The differences data set for the fasting and glucose intake variables Minitab 18 result output of Skewness and Kurtosis (See JB’s computation in Table 4.1).

Descriptive Statistics: d1, d2, d3, d4, d5, d6

Variable                 Skewness               Kurtosis

d1                           -0.11                       2.41

d2                            0.50                       1.42

 d3                            0.51                      -0.05

d4                            0.76                       0.07

 d5                            0.75                      -0.05

 d6                            2.82                      10.04

Appendix C

Paired Observation tests of Diabetic Patients (α=99%

Paired T-Test and CI: 1st hr, Initial value

Paired T for 1st hr - Initial value

                                N             Mean                     StDev                     SE Mean

1st hr                    47         101.234               13.795                 2.012

Initial value          47           98.830                   13.921                   2.031

Difference             47           2.40426                              9.00642              1.31372

99% CI for mean difference: (-1.12573, 5.93424)

T-Test of mean difference = 0 (vs not = 0): T-Value = 1.83 P-Value = 0.074

Paired T-Test and CI: 2nd hr, 1st hr

Paired T for 2nd hr - 1st hr

                                N             Mean                     StDev                     SE Mean

2nd hr                    47           106.596                 13.812                   2.015

1st hr                      47           101.234                 13.795                   2.012

Difference             47           5.36170                              8.78592                         1.28156

99% CI for mean difference: (1.91814, 8.80527)

T-Test of mean difference = 0 (vs not = 0): T-Value = 4.18 P-Value = 0.000

 Paired T-Test and CI: 2nd hr, Initial value

Paired T for 2nd hr - Initial value

                                N             Mean     StDev         SE Mean

2nd hr                                    47           106.596  13.812         2.015

Initial value          47           98.830   13.921                         2.031

Difference             47           7.76596  13.97080      2.03785

99% CI for mean difference: (2.29023, 13.24169)

T-Test of mean difference = 0 (vs not = 0): T-Value = 3.81 P-Value = 0.000

 Paired T-Test and CI: 1st hr after taken glucose, 2nd hr

Paired T for 1st hr after taken glucose - 2nd hr

                                N             Mean                     StDev                     SE Mean

1st hr after tak     47           186.213                 31.700                   4.624

2nd hr                                    47           106.596                 13.812                   2.015

Difference             47           79.6170                 30.514                   4.4510

99% CI for mean difference: (67.6570, 91.5770)

T-Test of mean difference = 0 (vs not = 0): T-Value = 17.89 P-Value = 0.000

Paired T-Test and CI: 2nd hr after taken glucose, 2nd hr

Paired T for 2nd hr after taken glucose - 2nd hr

                                                N             Mean                     StDev                     SE Mean

2nd hr after tak                    47           191.766                 35.105                  5.121

2nd hr                                                    47           106.596                 13.812                   2.015

Difference                             47           85.1702                                 33.7441                                 4.9221

99% CI for mean difference: (71.9445, 98.3959)

T-Test of mean difference = 0 (vs not = 0): T-Value = 17.30 P-Value = 0.000

 Paired T-Test and CI: 2nd hr after taken glucose, 1st hr after taken glucose

Paired T for 2nd hr after taken glucose - 1st hr after taken glucose

                                N             Mean                     StDev                     SE Mean

2nd hr after tak    47           191.766                 35.105                   5.121

1st hr after tak     47           186.213                 31.700                   4.624

Difference             47           5.55319                                 9.83076                                 1.43396

99% CI for mean difference: (1.70011, 9.40627)

T-Test of mean difference = 0 (vs not = 0): T-Value = 3.87 P-Value = 0.000

Wilcoxon Signed Rank Test: d1

Test of median = 0.000000 versus median not = 0.000000

    N for Wilcoxon    Estimated    N Test Statistic    P  Median

d1           47                          44           656.5 0.060          2.500

Wilcoxon Signed Rank Test: d2

Test of median = 0.000000 versus median not = 0.000000

                 N for Wilcoxon    Estimated     N Test Statistic     P  Median

d2                           47                  46               910.0 0.000                5.000

Wilcoxon Signed Rank Test: d3

Test of median = 0.000000 versus median not = 0.000000

                N for Wilcoxon    Estimated       N Test Statistic      P  Median

d3                           47                 45                825.0 0.001               6.500

Wilcoxon Signed Rank Test: d4

Test of median = 0.000000 versus median not = 0.000000

                N for Wilcoxon    Estimated       N Test Statistic     P  Median

d4                           47                  47                1128.0 0.000            77.50

Wilcoxon Signed Rank Test: d5

Test of median = 0.000000 versus median not = 0.000000

                N for Wilcoxon    Estimated              N Test Statistic     P  Median

d5                           47                47                       1128.0 0.000          83.00

Wilcoxon Signed Rank Test: d6

Test of median = 0.000000 versus median not = 0.000000

                N for Wilcoxon     Estimated       N Test Statistic    P  Median

d6                    47                         44                  870.0 0.000            4.000

Sign Test for Median: d1

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal     Above   P Median

d1           47           14           3  30       0.0226   2.000

Sign Test for Median: d2

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal     Above   P Median

  d2         47           9              1  37       0.0000   5.000

Sign Test for Median: d3

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal     Above   P Median

d3           47           12           2  33       0.0025   5.000

Sign Test for Median: d4

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal     Above   P Median

d4           47           0              0  47       0.0000  72.00

Sign Test for Median: d5

Sign test of median = 0.00000 versus not = 0.00000

                 N            Below     Equal     Above   P Median

d5           47           0              0  47       0.0000   76.00

Sign Test for Median: d6

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal     Above   P Median

d6           47           8              3  36       0.0000   4.000

Appendix D

Paired Observation tests of Diabetic Patients (

Paired T-Test and CI: 1st hr, Initial value

Paired T for 1st hr - Initial value

                                N             Mean     StDev     SE Mean

1st hr                      47           101.234 13.795  2.012

Initial value          47           98.830   13.921   2.031

Difference             47           2.40426 9.00642 1.31372

95% CI for mean difference: (-0.24013, 5.04864)

T-Test of mean difference = 0 (vs not = 0): T-Value = 1.83 P-Value = 0.074

Paired T-Test and CI: 2nd hr, 1st hr

Paired T for 2nd hr - 1st hr

                                N             Mean                     StDev                     SE Mean

2nd hr                    47           106.596                 13.812                   2.015

1st hr                      47           101.234                 13.795                   2.012

Difference             47           5.36170                 8.78592                                 1.28156

95% CI for mean difference: (2.78206, 7.94135)

T-Test of mean difference = 0 (vs not = 0): T-Value = 4.18 P-Value = 0.000

Paired T-Test and CI: 2nd hr, Initial value

Paired T for 2nd hr - Initial value

                                N             Mean                     StDev                     SE Mean

2nd hr                    47           106.596                 13.812                   2.015

Initial value          47           98.830                   13.921                   2.031

Difference             47           7.76596                                 13.97080               2.03785

95% CI for mean difference: (3.66398, 11.86794)

T-Test of mean difference = 0 (vs not = 0): T-Value = 3.81 P-Value = 0.000

 Paired T-Test and CI: 1st hr after taken glucose, 2nd hr

Paired T for 1st hr after taken glucose - 2nd hr

                                N                             Mean                     StDev                     SE Mean

1st hr after tak     47                           186.213                 31.700                   4.624

2nd hr                                    47                           106.596                 13.812                   2.015

Difference             47                           79.6170                                 30.5148                                 4.4510

95% CI for mean difference: (70.6575, 88.5765)

T-Test of mean difference = 0 (vs not = 0): T-Value = 17.89 P-Value = 0.000

Paired T-Test and CI: 2nd hr after taken glucose, 2nd hr

Paired T for 2nd hr after taken glucose - 2nd hr

                                                N             Mean                     StDev                     SE Mean

2nd hr after tak                    47           191.766                 35.105                   5.121

2nd hr                                    47           106.596                 13.812                   2.015

Difference                             47           85.1702                                 33.7441                 4.9221

95% CI for mean difference: (75.2626, 95.0779)

T-Test of mean difference = 0 (vs not = 0): T-Value = 17.30 P-Value = 0.000

Paired T-Test and CI: 2nd hr after taken glucose, 1st hr after taken glucose

Paired T for 2nd hr after taken glucose - 1st hr after taken glucose

                                                N             Mean                     StDev                     SE Mean

2nd hr after tak                    47           191.766                 35.105                   5.121

1st hr after tak                     47           186.213                 31.700                   4.624

Difference                             47           5.55319                                 9.83076                                 1.43396

95% CI for mean difference: (2.66677, 8.43961)

T-Test of mean difference = 0 (vs not = 0): T-Value = 3.87 P-Value = 0.000

Wilcoxon Signed Rank Test: d1

Test of median = 0.000000 versus median not = 0.000000

                N for  Wilcoxon    Estimated        N Test Statistic    P Median

d1                    47                         44                  656.5 0.060             2.500

Wilcoxon Signed Rank Test: d2

Test of median = 0.000000 versus median not = 0.000000

                N for  Wilcoxon        Estimated         N Test Statistic   P Median

d2                    47                            46                  910.0 0.000         5.000

Wilcoxon Signed Rank Test: d3

Test of median = 0.000000 versus median not = 0.000000

          N for  Wilcoxon    Estimated    N Test Statistic   P Median

d3              47                        45                825.0 0.001        6.500

Wilcoxon Signed Rank Test: d4

Test of median = 0.000000 versus median not = 0.000000

       N for  Wilcoxon     Estimated     N Test Statistic     P Median

d4             47                         47              1128.0 0.000        77.50

Wilcoxon Signed Rank Test: d5

Test of median = 0.000000 versus median not = 0.000000

    N for  Wilcoxon    Estimated  N Test Statistic    P Median

d5           47                           47           1128.0 0.000        83.00

Wilcoxon Signed Rank Test: d6

Test of median = 0.000000 versus median not = 0.000000

          N for  Wilcoxon    Estimated    N Test Statistic       P Median

d6              47                        44                  870.0 0.000          4.000

Sign Test for Median: d1

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal     Above     P Median

d1           47           14           3  30       0.0226     2.000

Sign Test for Median: d2

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal Above        P Median

d2           47           9  1         37 0.0000              5.000

Sign Test for Median: d3

Sign test of median = 0.00000 versus not = 0.00000

N             Below     Equal Above        P Median

d3           47           12  2       33 0.0025              5.000

Sign Test for Median: d4

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal Above        P Median

d4           47           0  0         47 0.0000              72.00

Sign Test for Median: d5

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal Above        P Median

d5           47           0  0         47 0.0000              76.00

Sign Test for Median: d6

Sign test of median = 0.00000 versus not = 0.00000

N             Below     Equal Above        P Median

d6           47           8  3         36 0.0000              4.000

Appendix E

Paired Observation tests of Diabetic Patients (

Paired T-Test and CI: 1st hr, Initial value

Paired T for 1st hr - Initial value

N             Mean       StDev      SE Mean

1st hr                      47           101.234  13.795     2.012

Initial value          47           98.830     13.921    2.031

Difference             47          2.40426   9.00642  1.31372

90% CI for mean difference: (0.19896, 4.60955)

T-Test of mean difference = 0 (vs not = 0): T-Value = 1.83 P-Value = 0.074

Paired T-Test and CI: 2nd hr, 1st hr

Paired T for 2nd hr - 1st hr

                                N             Mean         StDev     SE Mean

2nd hr                    47           106.596   13.812                      2.015

1st hr                      47           101.234    13.795       2.012

Difference             47           5.36170    8.78592     1.28156

90% CI for mean difference: (3.21040, 7.51300)

T-Test of mean difference = 0 (vs not = 0): T-Value = 4.18 P-Value = 0.000

Paired T-Test and CI: 2nd hr, Initial value

Paired T for 2nd hr - Initial value

                                N             Mean        StDev         SE Mean

2nd hr                                    47           106.596     13.812        2.015

Initial value          47           98.830       13.921        2.031

Difference             47           7.76596     13.97080     2.03785

90% CI for mean difference: (4.34510, 11.18682)

T-Test of mean difference = 0 (vs not = 0): T-Value = 3.81 P-Value = 0.000

Paired T-Test and CI: 1st hr after taken glucose, 2nd hr

Paired T for 1st hr after taken glucose - 2nd hr

                                N             Mean     StDev     SE Mean

1st hr after tak     47           186.213  31.700    4.624

2nd hr                                    47           106.596  13.812    2.015

Difference             47           79.6170  30.5148  4.4510

90% CI for mean difference: (72.1452, 87.0888)

T-Test of mean difference = 0 (vs not = 0): T-Value = 17.89 P-Value = 0.000

Paired T-Test and CI: 2nd hr after taken glucose, 2nd hr

Paired T for 2nd hr after taken glucose - 2nd hr

                                                N             Mean     StDev     SE Mean

2nd hr after tak                    47           191.766  35.105    5.121

2nd hr                                                    47           106.596  13.812                    2.015

Difference                             47           85.1702                  33.7441  4.9221

90% CI for mean difference: (76.9077, 93.4327)

T-Test of mean difference = 0 (vs not = 0): T-Value = 17.30 P-Value = 0.000

Paired T-Test and CI: 2nd hr after taken glucose, 1st hr after taken glucose

Paired T for 2nd hr after taken glucose - 1st hr after taken glucose

                                                N             Mean       StDev          SE Mean

2nd hr after tak                    47           191.766    35.105        5.121

1st hr after tak                     47           186.213    31.700        4.624

Difference                             47           5.55319                   9.83076       1.43396

90% CI for mean difference: (3.14605, 7.96033)

T-Test of mean difference = 0 (vs not = 0): T-Value = 3.87 P-Value = 0.000

Wilcoxon Signed Rank Test: d1

Test of median = 0.000000 versus median not = 0.000000

    N for Wilcoxon    Estimated       N Test Statistic   P Median

d1                           47                    44                    656.5 0.060         2.500

Wilcoxon Signed Rank Test: d2

Test of median = 0.000000 versus median not = 0.000000

    N for  Wilcoxon    Estimated     N Test Statistic    P Median

d2           47                           46           910.0 0.000          5.000

Wilcoxon Signed Rank Test: d3

Test of median = 0.000000 versus median not = 0.000000

        N for  Wilcoxon     Estimated    N Test Statistic    P Median

d3           47                           45                825.0 0.001        6.500

Wilcoxon Signed Rank Test: d4

Test of median = 0.000000 versus median not = 0.000000

       N for  Wilcoxon     Estimated    N Test Statistic   P Median

d4           47                           47             1128.0 0.000      77.50

Wilcoxon Signed Rank Test: d5

Test of median = 0.000000 versus median not = 0.000000

       N for  Wilcoxon    Estimated    N Test Statistic   P Median

d5           47                           47           1128.0 0.000        83.00

Wilcoxon Signed Rank Test: d6

Test of median = 0.000000 versus median not = 0.000000

        N for  Wilcoxon    Estimated    N Test Statistic    P Median

d6               47                       44              870.0 0.000         4.000

Sign Test for Median: d1

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal Above      P Median

d1           47           14  3       30 0.0226              2.000

Sign Test for Median: d2

Sign test of median = 0.00000 versus not = 0.00000

                 N            Below     Equal Above   P Median

d2           47             9  1       37 0.0000         5.000

Sign Test for Median: d3

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal Above    P Median

d3           47            12  2       33 0.0025           5.000

Sign Test for Median: d4

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal Above     P Median

d4           47             0  0          47 0.0000           72.00

Sign Test for Median: d5

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal Above     P Median

d5           47             0  0         47 0.0000            76.00

Sign Test for Median: d6

Sign test of median = 0.00000 versus not = 0.00000

                N             Below     Equal Above    P Median

d6           47             8  3         36 0.0000            4.000

Appendix F

Two sample t- test between d₃ = x₃ – x₁ and d₄ = y₁ – x₃,

Mean of d3 =(x₃-x₁)

Mean of d3 = 7.46809

Mean of d4 =(y₁-x₃)

Mean of d4 = 73.7872

Standard Deviation of d3 =(x₃-x₁)

Standard deviation of d3 = 13.3853

Standard Deviation of d4 =(y₁-x₃)

Standard deviation of d4 = 30.4695

Two-Sample T-Test and CI: d3, d4

Two-sample T for d3 vs d4

N  Mean   StDev  SE   Mean

d3  47      7.5      13.4  2.0

d4  47      73.8    30.5  4.4

Difference = mu (d3) - mu (d4)

Estimate for difference: -66.3191

95% CI for difference: (-75.9604, -56.6779)

T-Test of difference = 0 (vs not =): T-Value = -13.66, P-Value = 0.000, DF = 92

Both use Pooled StDev = 23.5325