Statics and Dynamics of Malaria Transmission: The Relationship between Prevalence in Humans and Mosquitoes
Santiago Movilla Blanco
System Dynamics Group, Department of Geography, University of Bergen, Bergen, Norway
Corresponding author: Santiago Movilla Blanco, System Dynamics Group, Department of Geography, University of Bergen, Bergen, Norway.
Received: 07 June 2022; Accepted: 15 June 2022; Published: 29 June 2022
Article Information
Citation: Santiago Movilla Blanco. Statics and Dynamics of Malaria Transmission: The Relationship between Prevalence in Humans and Mosquitoes. Fortune Journal of Health Sciences 5 (2022): 374-406.
View / Download Pdf Share at FacebookAbstract
The present paper explores a simple dynamic model from which we review the classic formulae in malaria epidemiology that relate entomological and epidemiological variables to malaria transmission. In addition, we document the dynamics of malaria, illustrating the impact of control strategies and how the bites per mosquito have a larger effect on transmission intensity than the mosquito mortality, the ratio of mosquitoes to humans, or the transmission efficiency. The model has been built following the System Dynamics methodology, explicitly representing the variables, the feedbacks and the nonlinearities, i.e. the structure that governs the dynamics of the disease. In this sense, the paper offers a new way to obtain the most representative malaria indicators derived from stock-and-flow diagrams that encompass the causal relationships that exist between the attributes of such a system. Based on the obtained formulae from the human and mosquito sectors, we are able to eliminate three degrees of freedom, allowing us to calculate the temporal steady state relationship between Plasmodium falciparum prevalence in humans and mosquitoes. The model is generic in nature and may be parameterized to portray a wide variety of locations, different malaria parasites, vector species, and to cater for seasonality. Given that the model includes the principle mechanisms of malaria transmission, it acts as a foundation for simulations that represent the dynamics between humans and mosquitoes. Such model has been developed based on a number of simplifying assumptions. To the extent possible, the validity of the model under these assumptions has been analyzed by way of mathematic equations.
Keywords
<p>System Dynamics, Malaria Model, Integrated Vector Management (IVM), Entomological Inoculation Rate (EIR)</p>
Article Details
1. Introduction
Malaria in humans is caused by 5 Plasmodium parasites: Plasmodium falciparum, P. vivax, P. malariae, P. ovale and P. knowlesi [1] https. Among all the species, P. falciparum is the most prevalent and dangerous malaria parasite. Only in Africa, where most of the malaria is concentrated, over 95% of episodes are caused by P. falciparum [2] https. Due to its impact worldwide, we have chosen to focus our analysis on the transmission of P. falciparum. The analysis would be similar, though not the same, for other malaria parasites. For example, infections by the variant, P. vivax are characterized by relapses of malaria arising from the persistent liver stage of the parasite (hypnozoites) [3] https, which results in a different model structure than the case of P. falciparum.
During the process of understanding the epidemiology of malaria and other infectious diseases, mathematical models have historically played an important role. Models provide concise quantitative descriptions of complicated, non-linear processes, and a method for relating the process of infection in individuals to the incidence of infection or disease in a population over time [4] https. The System Dynamics (SD) modeling methodology is well suited to address the dynamic complexity that characterizes many public health issues. This approach involves the development of computer simulation models that portray processes of accumulation and feedbacks and that may be tested systematically to find effective policies for overcoming policy resistance [5] https.
In line with health issues, mosquito control is one of the key components in the fight against malaria. To ensure an effective implementation of interventions to reduce malaria transmission, the SD methodology is suitable to develop decision-support tools. These tools can help policy makers in improving the design of strategies that maximize reduction in mosquito bites and minimize the costs of malaria reduction, greatly impacting on malaria transmission at local and national level. Given the simplicity and the purpose of this model, its comprehensiveness and extensiveness are limited. In this paper it only portrays epidemiological aspects of malaria transmission. However, the model can include a higher level of complexity. In addition, the model is easily adaptable and can be customized for any location where P. falciparum is prevalent. The structure is inspired by the Ross-Macdonald model of malaria transmission (Figure 01) [6] https, and it is divided in two sectors.
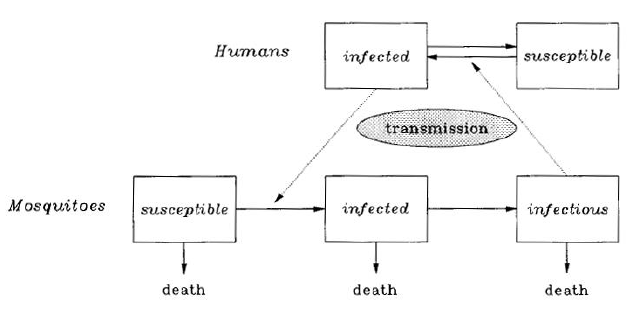
Figure 01
The first sector analyzes the humans and the second the mosquitoes. The common factor between the two sectors is humans and mosquitoes carrying the malaria parasite, i.e. P. falciparum. In this paper we will examine the simplest version of the model but covering the major aspects of malaria transmission.
2. Human Sector
The human sector portrays the dynamics of the different human states regarding malaria. We will first define the different variables involved, and later we will analyze the connection between them.
The figure 02 contains a list of variables with the abbreviations that we will use for the equations.

Figure 02
Some variables are named in a simplified way but we will describe one by one.
- Human Population (H): This refers to the total number of humans living in the area of analysis.
- Susceptible Humans (HS): We first define susceptible humans as persons clean from the malaria parasite and consequently susceptible to get infection with malaria if bitten by an infectious Anopheles mosquito.
- Infected Humans (HI): According to the WHO malaria terminology [7] https, malaria infected people are those with the presence of Plasmodium parasites in blood or tissues confirmed by diagnostic testing. Therefore, infected humans are the number of persons carrying P. falciparum parasites at a given point in time.
- Human Prevalence (PH): In epidemiology the prevalence of a certain disease is often defined as the number of individuals with infection at one time, but in our case we will define the prevalence in terms of proportion. Human prevalence is therefore defined as the population fraction that hosts parasitemia and it is obtained by dividing the infected humans HI by the total number of people H.
- Mosquito Prevalence (PM): Similarly to how we defined human prevalence, the mosquito prevalence is also a proportion, in this case, the proportion of infectious mosquitoes. This indicator is also known as Sporozoite Rate or in our case P. Falciparum Sporozoite Rate, which is the number of mosquitoes infected with sporozoites (the life parasite stage responsible for transmission from mosquito to human), divided by the total number of mosquitoes [8] https. In practice, the determination of sporozoite rates are obtained as the percentage of P. falciparum sporozoite positive mosquito samples out of the total number of mosquitoes analyzed [9] https.
- Vector Biting Rate (VR): This indicator is also known as the Human Biting Rate of the Anopheles mosquitoes, and it is calculated as the total number of indoor and outdoor mosquitoes caught biting humans during a 12-month sampling period divided by the number of people bitten (the catchers) [9]. Although its value is obtained through the number of mosquitoes caught biting humans, these mosquitoes also represent the number of bites received by a person during one year, and we can use the equivalent units of mosquito bites per person per year (bites/(person·year)). If the sampling period is not one year, we multiply the number of bites by the corresponding factor to make it annual. For example, if the bites are collected during a sampling period of four months, we will multiply the bites per person by three in order to express the bites in per annum units. It is important to note that this multiplication is only meant to adapt the units since the obtained Vector Biting Rate (VR) can only be used for the period during which it is valid. In fact, values obtained during wet seasons are likely to be higher than during dry seasons given that the rain normally involves increases in mosquito density.
-Entomological Inoculation Rate (EIR): The intensity of malaria parasite transmission is normally expressed as the entomological inoculation rate (EIR), the product of the vector biting rate times the proportion of mosquitoes infected with sporozoite-stage malaria parasites [10] https.
EIR is similarly defined as a measure of exposure to infectious mosquitoes. It is usually interpreted as the number of P. falciparum infective bites received by an individual during a season or in our case, annually [8]. Therefore, we refer to the annual entomological inoculation rate (AEIR), which is obtained by multiplying the average annual vector biting rate by the mosquito prevalence [9]. The equation for the EIR is indicated in (01) as the Vector Biting Rate (VR) multiplied by the Mosquito Prevalence (PM):

The units for this indicator are also bites per person per year, but the EIR refers only to the number of infectious bites. If we had a number for all the annual infectious bites in the area of analysis, the EIR would be the infectious bites per capita.
-Mosquito Infectivity (IM): Also known as transmission efficiency from mosquito to human, this variable is defined as the probability of an infectious mosquito to infect a susceptible human during blood-feeding. Normally, when a mosquito carrying sporozoites bites a susceptible human, there is 100% chance that the parasites will be passed to the individual. However, whether the host becomes infected or not depends on other factors that might reduce mosquito infectivity. For example, it has been long assumed that the probability of mosquito-to-human transmission is determined simply by the presence of salivary gland sporozoites. However, the number of parasites injected in the course of a bite might influence the probability of disease transmission [11] https.
In summary, assuming a bite from an infectious mosquito, we can define mosquito infectivity as the probability that sporozoites are being inoculated and that they invade the liver cells of the host, so as to initiate the infection process
The unit for this variable is the fraction of a person infected per bite. Its maximum value would be 1, in which case every bite by an infectious mosquito affecting a susceptible human would cause a human infection. In such a case, the incidence or number of malaria infections per year would be the EIR multiplied by the number of susceptible humans.
-Average Recovery Time (TR): This is the average time between human infection and clearance of parasites in the blood. In our model an infected person becomes susceptible again after this time. If after an infection the person becomes susceptible and has developed immunity to become infected again, this would be reflected in the reduction of the mosquito infectivity. This variable is calculated as the weighted average of the recovery time for persons who experience the malaria symptoms and recover shortly after prompt treatment, and the recovery time for asymptomatic infections, which normally are not treated and therefore are prolonged over a significant period of time. In general, it takes around two weeks of treatment to recover from malaria. But without clinical illness, asymptomatic infections are silent and remain untreated, resulting in chronic carriage that can last for 6 months or longer [12] https. In this sense, a study conducted in an area of high P. falciparum transmission in Ghana, estimated that untreated asymptomatic infections had a mean duration of 194 days (0.53 years) [13] https.
We will obtain a more elaborated calculation of this variable later as we increase the complexity of our model. In order to keep consistency with the model, the time units for recovery time are in years. Once defined the first list of variables, we can interrelate them in a model diagram (Figure 03). Stocks are represented by rectangles while the thick arrows represent the flows between the stocks. The regular (blue) arrows represent causal relationships between two variables, i.e. a cause and an effect. The polarities next to the regular arrows (plus or minus) indicate the polarity of the causality (positive or negative). For example, an increase in the entomological inoculation rate (EIR) increases the malaria incidence (positive polarity). On the contrary, an increase in recovery time reduces the flow of recoveries (negative polarity).
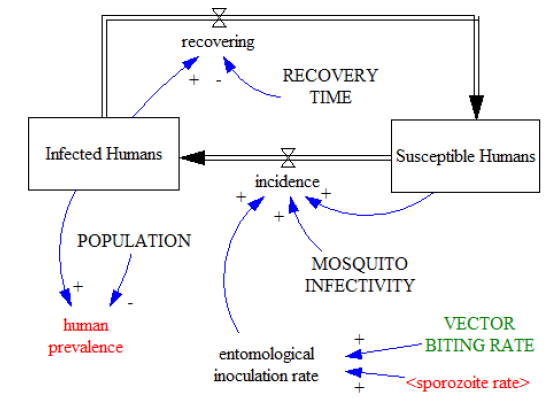
Figure 03
As in the Ross-Macdonald model, there are two stocks, one representing the susceptible population and the other one representing the infected population. People are transferred from susceptible humans to infected humans through the flow of incidence, which is defined as the number of new malaria cases during a defined period. In our case the period is one year so that we consider annual infections with units in persons/year.
The persons in the stock of infected humans eventually recover through the flow of recovering, (also in units of persons/year), transferring from infected back to susceptible. In this case, the flow of recoveries is determined by the two elements from which it gets linking arrows. In this case recovering is defined as the stock on infected humans divided by the average recovery time.
In equilibrium, the number of infections and recoveries are similar so as to keep the stock values relatively constant over time. This means we could assume both flows with same values over time (incidence = recovering).
(In this model the human prevalence (PH) is calculated as a fraction, dividing the stock of infected humans by the total population as explained previously. However, in the epidemiology literature, human prevalence is also referred as the number of individuals with infection at one time. If using this definition, the human prevalence in our model would be equal to the stock of infected humans. In such a case, the number of recoveries would be equal to prevalence divided by recovery time, and since in equilibrium recovering must be equal to incidence, then incidence would be also equal to prevalence divided by recovery time. As a result, prevalence would be the incidence multiplied by the recovery time (Prevalence = Incidence · Recovery Time). This is a formula used in epidemiology and we can observe that it fits with the structure of our preliminary model.)
The rest of equations associated to the model structure in figure 02 are determined as follows:
Since human prevalence (PH) is equal to Infected Humans (HI) divided by all humans (H), then infected humans is the prevalence multiplied by total number of humans (H). Moreover, the susceptible population (HS) is the total humans minus those infected:
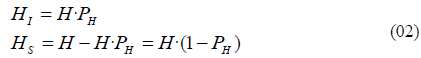
As indicated before, the flow of recoveries is defined as the stock of infected humans divided by average recovery time (TR). The flow of incidence or annual infections is defined as the susceptible population multiplied by the annual infectious bites per person (EIR), and then again multiplied by the mosquito Infectivity (IM). Substituting definitions from (02) we obtain the following equations:
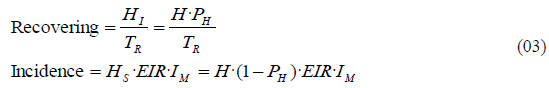
Considering that the system is in equilibrium, incidence must be equal to recovering. Assuming equilibrium from (03) we thus obtain the following equations:
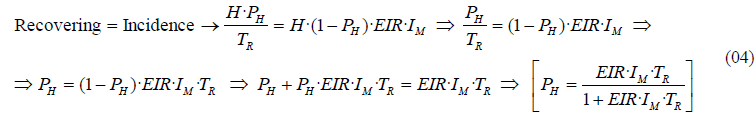
The resulting equation in (04) relates human prevalence with the EIR, conditioned by the values of recovery time and mosquito infectivity. This relationship between EIR and the proportion of humans with parasitemia can be seen unfold in the next graph (Figure 04), where we have assumed IM=1 person/bite and a TR=0.25 years, i.e. 3 months.
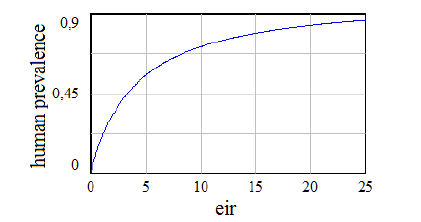
Figure 04
The shape of this graph is the same as the obtained in other mathematical studies [4], and also matches with graphs of this relationship obtained empirically [14] https.
If we substitute the equation (01) that defines EIR, into the equation (04), we obtain the following expression for human prevalence PH:
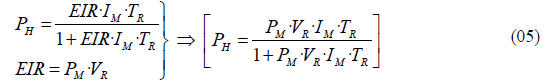
From this formula we can also derive the value of the vector biting rate VR, assuming that we know the remaining variables:
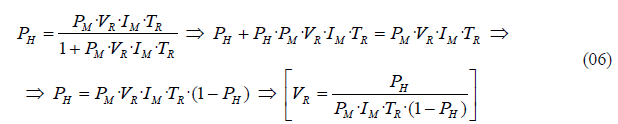
For simplicity, and given that we consider a steady state model or model in equilibrium, we can ignore births and deaths as the total human population size does not experience major changes during the observation period. In fact, the assumption that a population is in a dynamic equilibrium and that it has a stationary age distribution is frequently violated in practice, but it provides a useful starting point for a more sophisticated analysis [4]. In more complex versions of the model, we have included human births and deaths. But even after implementing a dynamic population that varies over time, the final equations that relate human and mosquito prevalence still provide very similar results to the ones we just obtained when considering the equilibrium condition. This similitude is principally caused by the part of the model that represents the mosquito populations, which operates with units in mosquitoes per person, and consequently produces very similar results regardless of a changing number of persons.
3. Mosquito Sector
As we did in the human sector, we will first define the different variables involved, and later we will analyze the connection between them.
The figure 05 contains a list of variables with the abbreviations that we will use for the equations.

Figure 05
-Annual Bites per Mosquito (BR): Also known as human feeding rate, this indicator represents the average number of bites on humans per mosquito and per year. Anopheles mosquitoes can also take their blood meals from other animals, but those bites do not count as part of our annual bites per mosquito. Therefore, among other factors, this value also depends on the human blood index (HBI), which represents the proportion of blood meals derived from humans relative to all meals, or also defined as the proportion of mosquitoes that have fed on humans out of total fed [7].
If we consider the average life expectancy of adult female mosquitoes around three weeks [15] https, the annual bites would be equal to the bites by a consecutive series of mosquito’s during their lifetime, multiplied by the number of three-week periods in one year. Therefore, the annual bites do not depend on the mosquito longevity and represent the level of human biting activity during a mosquito lifetime. The units are in bites/(mosquito·year), and its value also represents the mosquito feeding frequency, which is the inverse of the feeding cycle duration, or average time spend by a mosquito between two consecutive meals.
The human feeding rate is only applicable to adult female Anopheles mosquitoes, which are the blood feeding mosquitoes responsible for malaria transmission. Depending on the conditions, female mosquitoes would normally search for a blood meal every 2-3 days [16] https, resulting in around 150 bites per year. However, these bites are distributed across different animal species and the number of bites on humans is just a fraction of the total (This fraction is actually indicated by the human blood index (HBI)). Later in the current section, the bites per mosquito will be calculated mathematically in the model, using as a reference other variables which can be obtained empirically.
-Biting Mosquitoes per Person (M): This variable represents a way to quantify the mosquito density in the area of analysis. There are various methods as replacement of human landing catches (HLC) for mosquito sampling [17] https. However, in our case the biting mosquitoes per person are obtained mathematically from the observed Vector Biting Rate (VR), which we already defined as the annual number of mosquitoes caught biting humans divided by the number of people bitten, with units in bites/(person·year).
If we were able to multiply the bites per mosquito (BR) by all the biting mosquitoes per person (M), it would result in the total number of bites received by one individual, which is precisely our Vector Biting Rate. Therefore, as indicated in (07), the number of biting mosquitoes per person is the result from dividing all the bites per person (VR) by the bites per mosquito (BR).
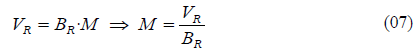
Out of the three indicators included in (07), we consider the Vector Biting Rate (VR) as the only known indicator by observation. The female Anopheles mosquitoes that have never bitten humans are not recorded through the Vector Biting Rate (VR), but they are indirectly recorded as a portion of the denominator in the mosquito prevalence (PM), and they are also part of the Biting Mosquitoes per Person (M) because they contribute to a reduction of the average number of bites per mosquito (BR). Later in this section we will calculate the Annual Bites per Mosquito (BR) and the Biting Mosquitoes per Person (M) during the explanation of the model equations for the mosquito sector.
-Infectious Mosquitoes per Person (MI): Out of the total mosquitoes per person (M), the infectious mosquitoes are those that are able to transmit malaria. We can obtain this number multiplying mosquitoes per person (M) by the mosquito prevalence (PM), as indicated in (08).

-Susceptible Mosquitoes per Person (MS): For the moment we will assume that susceptible mosquitoes are the total mosquitoes (M) minus the infectious (MI). Using the result in (08) we determine MS by following the next equation:
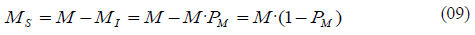
We know that mosquitoes develop infectiousness by going through a process from susceptible to infections. During that process, the mosquitoes are in an intermediate state called exposed mosquitoes, where they are neither infectious nor susceptible. Therefore, during the process of becoming infectious they remain infected until they die or until they actually become infectious. Later in the chapter 3.2, we will include a more complex model with exposed mosquitoes and explain why this preliminary assumption is valid for our analysis, but for now we will assume that the exposed mosquitoes are part of the stock of susceptible mosquitoes.
-Time to Develop Sporozoites (TP): In the case of a mosquito becoming infectious, this variable represents the period of time between the bite to a human carrying gametocytes (the life stage of the parasite that do not cause disease symptoms, but is responsible for onward transmission to mosquitoes), and the presence of sporozoites in the salivary glands of the mosquito. After this time the mosquito is infectious and ready to transmit malaria. TP is also known as extrinsic incubation period or entomological incubation period, defined as the length of the period from ingestion of gametocytes to becoming infectious [4]. Its value depends on many factors but most sporozoite infections do not appear until 10 or more days after blood-feeding [18] https.
-Average Life Expectancy of Adult Mosquitoes (TM): As mentioned before, the average life expectancy of an adult female Anopheles is around three weeks [15]. This is the period during which the mosquitoes are able to bite humans.
-Average Life Expectancy of Exposed Mosquitoes (TE): We will use this variable after introducing the model that includes the stock of exposed mosquitoes. This is the average lifetime of the mosquitoes that already initiated the infection process. The mosquitoes seek blood meals very early after becoming adults. Immediately following adult emergence, there is period of one or two days during which host-seeking behavior first begins to be expressed [19] https. In this sense, the bite that triggers the infection of a mosquito could happen almost any time during its entire adult life. Some mosquitoes could perform that bite in their early days and others at the very end of their lifespan.
If a susceptible mosquito performs the infective bite at the beginning of its adult life, the remaining life expectancy will be close to the average life expectancy of an adult mosquito i.e. three weeks. However, if the infective bite is produced shortly before it dies, the remaining life expectancy would be very brief.
- Average Life Expectancy of Infectious Mosquitoes (TI): This is the average lifetime of a mosquito that has become infectious. Considering the average life expectancy of an adult mosquito (TM) and the time to develop sporozoites (TP), the life expectancy of an infectious mosquito (TI) is, on the average, shorter than the average life expectancy of an exposed mosquito.
Following the same logic as for exposed mosquitoes, the maximum average life expectancy of an infectious mosquito would be attained when the infective bite of such a mosquito takes place at the earliest possible day of its adulthood. In this case, the mosquito would become infectious after the extrinsic incubation period TP, and during the rest of its life it would remain infected. Other mosquitoes would become infectious during the last days of their lives, or will not live long enough to become infectious.
Depending on the feeding frequency and the mosquito infectivity, the average life expectancy would allow infectious mosquitoes to infect one or two persons at most. However, if the blood meals are interrupted, infectious mosquitoes could infect more people. This assumption is based on the fact that adult mosquitoes live around three weeks and their time to develop sporozoites is more than ten days, which means that even if picking infection in the very early days of adulthood, a mosquito would have less than a week to infect humans with malaria. This remaining time combined with feeding cycle duration of 2-3 days, would result in a maximum of 2 persons receiving an infective bite from this mosquito. Given that, in our model, all the units of time are in years, we need to convert the calculated days of life expectancy into years. To do that, we divide the longevities by a factor of 365 days/year.
-Human Infectivity (IH): Similarly defined as the mosquito infectivity in the human sector (probability of an infectious mosquito to infect a susceptible human during blood-feeding), we define human infectivity as the probability of a susceptible mosquito to pick up infection from an infected human during blood-feeding. In other words, this is the proportion of blood meals taken from infected humans which are infectious to mosquitoes. Its value ranges from 0 to 1 and the unit of measure for this variable is the fraction of mosquitoes infected per bite.
It is challenging to obtain the value of this variable: To begin with, from all the infected people that comprise the human prevalence, we need to consider only those who are infectious. But even if considering only infectious persons, there is no certainty that susceptible mosquitoes would become infected after biting such persons. A study in New Guinea determined that the mean percentage of mosquitoes that became infected by feeding on infectious people was 37.9% [20] https.
Given that from the human sector we only import human prevalence, we need to consider which part of this prevalence corresponds to infectious humans as part of the calculation of the human infectivity. In our case, infectious humans are those carrying mature P. falciparum gametocytes in the peripheral blood and in consequence making them available for uptake by a biting Anopheles mosquito [21] https. In this sense, gametocyte density might not be related to infectiousness. In one study they found some individuals with low gametocyte densities who were infective to mosquitoes, while others with abundant gametocytes did not infect [22] https. This result is from an old study and perhaps they did not take the maturity of the gametocytes into consideration. Consequently, it is important to keep in mind that not all gametocyte carriers are infectious, but only those with mature gametocytes in the peripheral blood.
In summary, the concept of malaria infectious and malaria infected are not the same. Malaria infectious implies carrying mature gametocytes while the definition of malaria infection just implies the presence of parasites confirmed by diagnostic testing, without specifying whether parasitemia is asexual (merozoites), sexual (gametocytes), or both. And as we indicated, not even all the identified gametocyte carriers are infectious. Therefore, we can make the assumption that all the individuals included in the malaria prevalence are potentially infectious, and human infectivity will be equal to the proportion of mosquitoes that pick up infection after biting a member of the human prevalence i.e. infected person. With the given premises, our human infectivity can be obtained through the multiplication of three factors: 1. Proportion of the prevalence carrying gametocytes, 2. Proportion of gametocyte carriers who are infectious, and 3. Proportion of susceptible mosquitoes becoming infected after biting an infectious person (or proportion of bites on infectious persons that triggers mosquito infection).
-Mosquito Infectious Rate (IR): Also known as transmission efficiency from human to mosquito, this last variable is related to the human infectivity that we just defined. If human infectivity is the probability of a susceptible mosquito to pick up infection from an infected human during blood-feeding, the mosquito infectious rate is the probability of a susceptible mosquito to become infectious after biting an infected human.
As in the human infectivity, the units are in mosquitoes/bite. But the difference between the two variables is that human infectivity refers to the fraction of mosquitoes becoming infected while mosquito infectious rate refers to the fraction of mosquitoes becoming infectious. Since the mosquitoes take some time to become infectious after picking up infection, many exposed mosquitoes die during the process, making the infectious rate (IR) significantly smaller than the human infectivity (IH).
The reason to use IR is that in this simple version of the model we do not include the stock of exposed mosquitoes so we connect directly susceptible with infectious through a flow of mosquitoes which is regulated by the infectious rate as seen in figure 06.
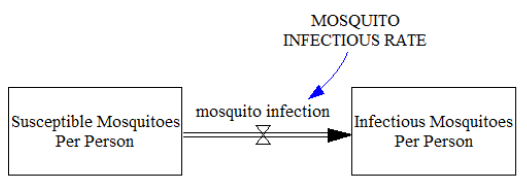
Figure 06
As a result, the susceptible mosquitoes remain in the stock of susceptible until they have plasmodium sporozoites in the salivary glands ready to inoculate on humans, making them infectious.
Later we well calculate mathematically the relationship between the Mosquito Infectious Rate and the Human Infectivity and demonstrate that this simple model gets similar results to the one including the intermediate stock of exposed mosquitoes, or mosquitoes developing infectiousness.
But before we proceed with this sector we need to add some considerations:
So far we have assumed that the infectious persons are part of the reported malaria positives, and consequently being also part of the prevalence. However, it is possible that part of the infectious population is not recorded as part of the prevalence because the given diagnostic testing did not detect parasitemia. These infectious individuals can be among the partially immune humans who have gametocytes present in the blood and could be infectious to mosquitoes, yet their parasites are undetected by certain diagnostic testing. There is actually evidence that chronic subpatent infections are a source of onward mosquito transmission of malaria. In semi-immune individuals with persistent infections, gametocytaemia at densities below the limit of microscopy detection is often infectious [23] https.
In this regard, one of the factors that determine parasite detection is the sensitivity of the diagnostic testing. High sensitivity tests can detect low parasite densities, but in most cases the prime concern of the detection methods is to identify asexual parasitemia, which is what causes the malaria symptoms and for which most treatments are deployed. The most spread identification method for malaria in Africa is the rapid diagnostic test (RDT) [24] https. Interestingly, while the aim is to detect the asexual parasites that cause the disease, RDTs can lead to positives with the mere presence of gametocytes in blood (we consider the most typical RDTs that test for either or both types of malaria antigens: histidine-rich protein II (HRP2); and Plasmodium lactate dehydrogenase (pLDH) enzyme) [25] https.
Detecting possible gametocyte carriers can be useful to identify potential infectious population, but when the result from a RDT only indicates positive or negative, the positive cannot establish whether detected parasitemia is asexual, sexual or both, and in consequence positives from this method can lead to wrong diagnosis and treatment.
For example, artemisinin-based combination treatments (ACTs) are now generally accepted as the best treatments for uncomplicated falciparum malaria [26] https. Apart from eliminating the merozoites, ACTs for falciparum malaria also reduce gametocyte carriage, and therefore reduce transmission, but artemisinin derivatives only acts against young gametocytes [27] http. Mature gametocytes are not affected by many antimalarial drugs and may thus be present long after asexual parasitemia has been cleared and the patient has recovered from the malaria symptoms [28] https.
If the RDTs used in the area of study detect mature gametocytes, we could assume that most potential infectious are within the measured prevalence. Should this assumption compromise significantly the accuracy of the results, we will use a parameter that adjusts the variables before implementing values into the model. The last consideration is about clarifying our definition of the recovery time (TR) in the human sector. As indicated before, TR is the average time between human infection and clearance of parasites in the blood. Consequently, the persons who recover from clinical symptoms after treatment but remain infectious are not considered susceptible. Therefore, our recovery period also includes the time that takes a person to clear mature gametocytes from peripheral blood circulation.
One trial demonstrated that gametocytes persist an average of 55 days after treatment with a non-ACT and 13.4 days after treatment with an ACT [29] https. These findings confirm that gametocytes may linger in peripheral blood up to several weeks after an asexual parasite infection has been cleared (whether by natural immunity or by drugs) [12].
The fact that our recovery time also includes gametocyte clearance is one of the reasons why we have not incorporated a stock with immune humans in this simple model. In general, it is important to incorporate immunity into malaria models in order to make them more realistic [6], but in our case we can incorporate them as part of the susceptible humans or as part of the infected, depending on the acquired immunity:
As mentioned before, in case of immune persons who are able to inhibit sporozoite inoculation and remain clean of parasites, we can include them in the stock of susceptible and consider their contribution in reducing the average mosquito infectivity. Although in general, people with naturally acquired immunity (NAI) still have parasitemia and we include them as infected. Sometimes, individuals that have been permanently exposed to the parasite develop specific immune responses capable of blocking parasite transmission to the mosquito vector. This is referred to as transmission blocking immunity [30] http. However, NAI does not appear to inhibit gametocytogenesis, since immune adults retain the capacity to infect mosquitoes and constitute a sizeable and important part of the available gametocyte reservoir [31] https.
In this sense, asymptomatic infections may be associated with a greater probability of gametocyte carriage, although there is also likely to be a lower density of gametocytes in these individuals, and these effects may cancel themselves out with respect to altering the infectivity of asymptomatic infections compared to symptomatic. [12]
But even in areas of low transmission, the contribution of asymptomatic infections to transmission is likely to be substantial, and in areas with seasonal transmission, asymptomatic infections may serve as the source of infections for a new generation of mosquitoes emerging after the start of the rains.
3.1 Simple Mosquito Sector
After dealing with the previous considerations, and once defined all the variables from the mosquito sector, we can see them linked in the next model diagram (Figure 07).
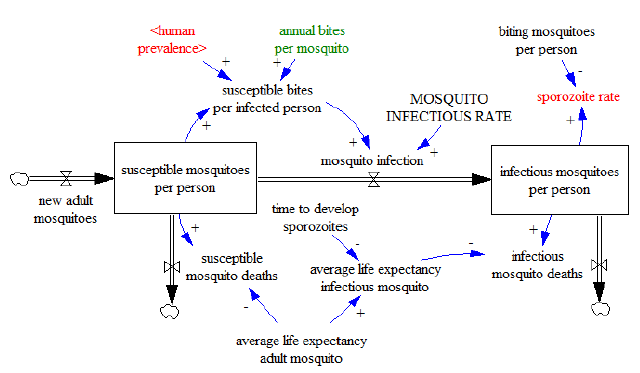
Figure 07
This sector is connected to the human sector through two indicators: From the human sector we import human prevalence and from the mosquito sector we export mosquito prevalence (sporozoite rate). These are actually the key indicators from the human and mosquito sector respectively. Note that while in the human sector the stocks include all the persons in the area of study, in this sector the stocks only include mosquito densities in units of mosquitoes per person, and as we mentioned, we only refer to malaria-bearing anophelines i.e. female adult Anopheles mosquitoes that can potentially transmit the malaria parasite.
The dynamics of this sector basically portray the transition of adult mosquitoes from being susceptible to being infectious, and their deaths in their different infective states. We assume a temporally constant density of mosquitoes per person in equilibrium, which implies that the number of mosquitoes dying is approximately equal to the emerged new mosquitoes. We achieve constant mosquito density in the model by replacing the dying mosquitoes with new adult mosquitoes. An increase or reduction of the mosquito density can take place by many factors, such as variation in rains or changes in the implementation of malaria control interventions. In a more complex version of the model it is possible to implement Integrated Vector Management (IVM) interventions [32] https and see what the outcome is. For example, spraying operations can kill indoor mosquitoes reducing their average life expectancy, while bed net usage can reduce the indoor vector biting rate by reducing the bites of indoor mosquitoes to humans.
In summary, unless additional interventions are implemented or deployed, we will consider a temporally constant mosquito density. In order to keep the densities in equilibrium, the stocks will be constant over time by making the inflows equal to the outflows. Therefore, the inflow of new adult mosquitoes will be equal to the sum of mosquito deaths. In order to initialize the value of the two stocks, we need to calculate mathematically the initial total biting mosquitoes per person M and then assign to each stock the corresponding part of these mosquitoes. Once we know the value of M, and knowing also the mosquito prevalence PM from observation, we can obtain the initial value of susceptible and infectious mosquitoes per person respectively by using the equations (08) and (09):
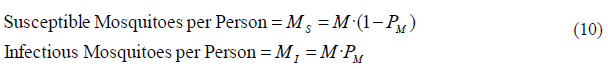
With the stock values we can calculate the mosquito deaths, which are the outflows in this sector. We calculate the susceptible mosquito deaths as the stock of susceptible mosquitoes MS divided by the life expectancy of adult mosquitoes TM, while the infectious mosquito deaths are equal to the stock of infectious mosquitoes MI divided by their life expectancy TI. Substituting susceptible and infectious mosquitoes from (10), we get the next equations for mosquito deaths, where the units are in mosquitoes/(person·year):
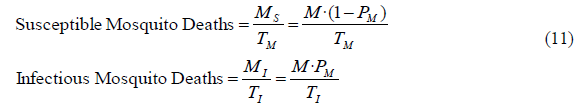
Note that since the mosquito prevalence PM is usually a very small number [14], most mosquitoes are susceptible, which means that the life expectancy of susceptible mosquitoes is practically the same as the life expectancy of the adult mosquitoes. In a later chapter where we calculate the mosquito life expectancy, we will deal with this small inaccuracy. The units for mosquito deaths are in mosquitoes/(person·year).
As we have indicated before, in temporal steady state all the mosquito deaths are replaced or substituted by new adult mosquitoes that emerge at the same rate. In this situation the adult mosquito death rate (1/TM) would be equal to the rate of emerging adult mosquitoes. Given that we are talking of a fractional death rate with units in 1/year, this term would be also valid for all the mosquitoes (not only mosquitoes per person), being representative of the current breeding and development capacity of the Anopheles mosquitoes in the area. In order to calculate the total biting mosquitoes per person M, we will operate similarly as we did in the human sector, where we also considered the system in temporal steady state. If we focus on the stock of infectious mosquitoes represented in figure 07, the equilibrium is reached when the mosquito infection inflow is the same as the outflow of infectious mosquito deaths, keeping constant the stock value MI. The flow of mosquito infections is produced by means of susceptible mosquito bites on infected humans. In order to obtain the flow of mosquito infection, we need to calculate first the number of susceptible bites to each infected human. Taking as a reference the stock of susceptible mosquitoes per person MS, the susceptible mosquito bites per person is obtained as the product of all susceptible mosquitoes per person times the bites per mosquito BR. Substituting BR from (07) and MS from (09) we get the next equation:
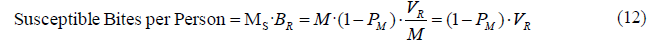
We observe from the result in (12) that the number of susceptible bites per person is actually the complementary of the infectious bites per person, defined in (01) as PM·VR, and equal to the entomological inoculation rate. The sum of susceptible bites plus infectious bites in this model would comprise the total number of bites per person (VR).
From all those mosquito bites we only want the bites performed on infected humans. Therefore, we need to multiply the resulting susceptible bites by the human prevalence, which is the fraction of infected humans. At this point we assume that all humans are the same attractive to mosquitoes. If infected humans are more attractive we would need to increase the proportion of bites on these people by adding a factor. Otherwise, the resulting expression of susceptible mosquito bites per infected person (SI) is shown in (13).
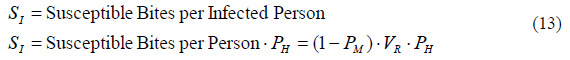
The last step in order to calculate the flow of mosquito infections is to consider the mosquito infectious rate IR, which is the probability of a susceptible mosquito to become infectious after biting an infected human.
So based on this probability, from all the bites made by susceptible mosquitoes on infected humans, we only consider the fraction that becomes infectious.
Therefore, the flow of mosquitoes becoming infectious is equal to the mosquito infectious rate IR, multiplied by the susceptible bites per infected person SI. The resulting equation is represented in (14) and the units are mosquitoes/(person·year).
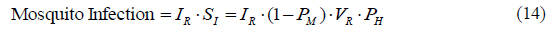
Coming back to the consideration of having the system in equilibrium, the stock of infectious mosquitoes will keep constant when its outflow is equal to its inflow. Therefore, the infectious mosquito deaths must be the same as the mosquito infection. Using the equations (11) and (14) and substituting we get the following expression that returns the mosquitoes per person M, also known as the ratio of mosquitoes to humans:
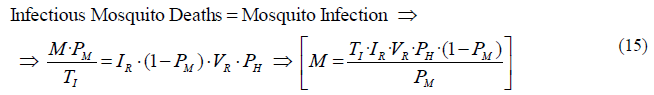
We observe in (15) that the biting mosquitoes per person M are calculated from variables that can be obtained empirically; some of them directly from observation (VR, PH and PM), and the other two (TI and IR) indirectly, using other variables also obtained by observation (The average life expectancy of infectious mosquito TI can be obtained using mosquito age distribution curves, and the infectious rate is derived from the human infectivity IH. The mosquito sector that contains the infection process will include how to calculate IR taking IH as a reference).
Once obtained M, and knowing the sporozoite prevalence, we can go back to the equations in (10) and set the initial value of the stocks.
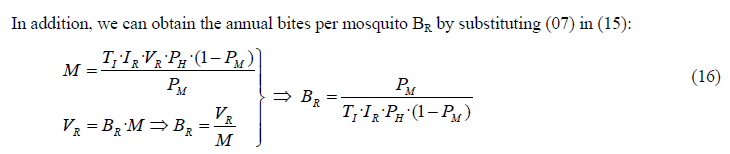
As we mentioned before, the intensity of malaria transmission is expressed through the EIR, which is equal to the vector biting rate times the mosquito prevalence (equation (01) where EIR=VR·PM). In turn, from (07) (VR=BR·M), the vector biting rate VR depends on both, BR and the mosquito density M. Therefore the EIR can be expressed in the following way:

In (18) we have deduced an alternative formula for EIR, determined as the annual bites per mosquito BR multiplied by the infectious mosquitoes per person MI. This multiplication logically results in the annual infectious bites received by any individual, which is precisely the definition of annual EIR. Finally, similarly as we calculated in (04) the equation for human prevalence, from (07) and (15) we can also obtain the mosquito prevalence depending on variables included in the mosquito sector:
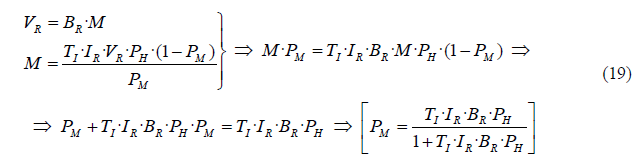
The expression in (19) is similar to (04), when we calculated human prevalence related to EIR. Both equations are in the format of y = Kx/(1+Kx). From (19) we can plot the relationship between mosquito and human prevalence in the next graph (Figure 08), where we assume the following values: VR=365 bites/(person·year), M=20 mosquitoes/person, TI=4 days (0.011 years) and IR=15% (0.15 mosquitoes/bite).
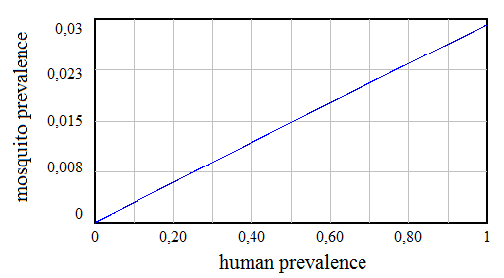
Figure 08
We observe in figure 8 that for the given values of some indicators, the maximum mosquito prevalence would be 2.9%, which is reached when the area of study becomes holoendemic (essentially every individual in the population is infected or the human prevalence is equal to 1).
Although the expressions for human prevalence (04) and mosquito prevalence (19) have the same format, their corresponding graphs (Figure 04 and figure 08) look different. Since the human prevalence can only range from 0 to 1, the function only works in an interval where the relationship between human and mosquito prevalence can be considered linear.
This linearity is due to the fact that even in the most favorable conditions for malaria transmission, the constant term of the equation (TI·IR·BR) is very small compared to 1. And since PH only ranges from 0 to 1, we can make the following approximation.
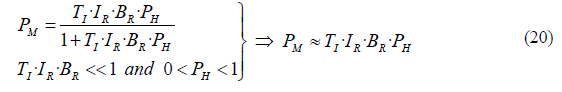
From this expression we can obtain the approximated relationship between Plasmodium falciparum prevalence in humans and mosquitoes:
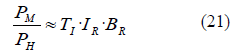
As a result, if we consider the term TI·IR as a constant that depends on the entomological and environmental conditions of the area, the ratio PM/PH is then proportional to the average bites on humans per mosquito BR. This also means that for a given human prevalence PH, the mosquito prevalence PM is proportional to BR.
As a summary, the presented analysis has derived the equations that would allow us to obtain the main root indicators for malaria transmission, which are VR, BR, M, PH and PM. Based on the established relationships from the equations, we are able to eliminate three degrees of freedom; one from the human sector, one from the mosquito sector, and another one from the equation that links both sectors, relating PH and PM. This means that we could obtain the value for the five indicators by knowing only two of them. Finally, based on the equations we can observe that all the indicators are obtained regardless of human population H. Therefore, the results are insensitive to the number of people and to different temporal steady state scenarios where human population has increased or decreased.
3.2 Mosquito Sector including the Infection Process
The main purpose of including the mosquito infection process is to determine the mosquito infectious rate (IR), and the mathematical relationship with the human infectivity (IH). The new diagram includes the transitory stock of infected mosquitoes per person and can be seen in the figure 09. Now some of the susceptible mosquitoes that bite infected humans initiate the infection process depending on the human infectivity and go to the stock of exposed mosquitoes where they remain until they die or until they become infectious after the time to develop sporozoites (TP). After developing sporozoites, which move to the salivary glands of the female Anopheles mosquito, mosquitoes become infectious, and in the model they move to the stock of infectious mosquitoes. Infectious mosquitoes are the only ones that can pass the parasite on to a susceptible human in the course of taking a blood meal.
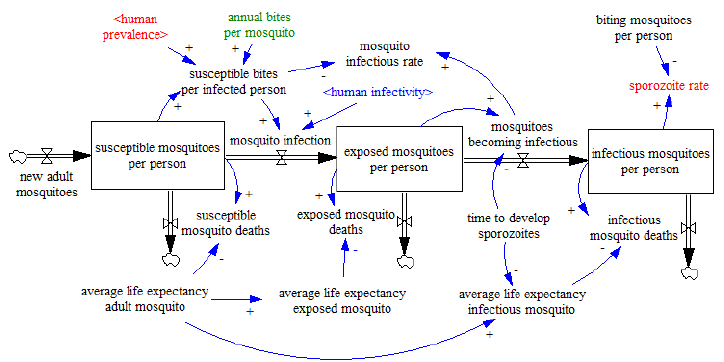
Figure 09
Like in the previous model, the susceptible and infectious mosquitoes per person are MS and MI respectively, with the corresponding average life expectancies expressed by TM for susceptible mosquitoes and TI for infectious mosquitoes. The new added stock contains the exposed mosquitoes per person ME, and TE is their corresponding life expectancy. Therefore, the outflow of deaths in each of the three stocks is the value of each stock divided by its average life expectancy. Also as in the previous model, we are set with a habitat of mosquitoes in temporal equilibrium which means that the inflow of new adult mosquitoes is equal to the sum of the three death outflows in order to keep constant the mosquito density.
The first variable we will deal with is the mosquito infectious rate (IR), and the mathematical relationship with human infectivity (IH). As we explained previously, human infectivity refers to the fraction of susceptible mosquitoes that, after biting an infected person, start the infection process. On the other hand, mosquito infectious rate is defined as the fraction of susceptible mosquitoes that, after biting an infected person, start the infection process and survive long enough to develop sporozoites in the salivary glands, becoming infectious. In the previous model, the susceptible mosquitoes picking up infection go directly to the stock of infectious mosquitoes. However, in this second version of the model, the mosquitoes go through the infection process at the stock of exposed mosquitoes, during which many of them might die before becoming infectious. As a result, the fraction of mosquitoes becoming infectious is significantly smaller than the fraction of mosquitoes starting the infection process, and in consequence, the mosquito infectious rate is smaller than the human infectivity.
In (13) we calculated the annual susceptible bites per infected person (SI), which is equally valid for this model. However, in this model the flow of mosquito infection represented in figure 09 is equal to SI multiplied by the human infectivity, which is the fraction of those bites that trigger mosquito infection, or also the fraction of susceptible mosquitoes becoming infected after biting an infected person. Consequently, SI multiplied by the human infectivity results in the flow of mosquitoes per person that start or initiate the infection process.
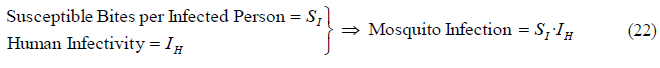
From (22), the human infectivity can be also defined as the number of mosquitoes that pick up infection, out of the total susceptible mosquitoes biting on infected humans.
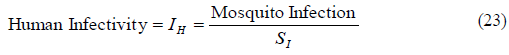
Unlike the human infectivity, the mosquito infectious rate is the number of mosquitoes becoming infectious, out of the total susceptible mosquitoes biting on infected humans.
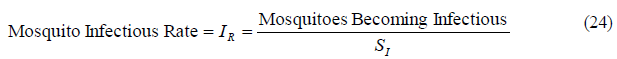
Taking now the stock of exposed mosquitoes as the reference, and considering the equilibrium condition, the inflow to this stock has to be equal to the sum of the outflows, where the inflow is the mosquito infection and the outflows are the exposed mosquito deaths, and the mosquitoes becoming infectious.
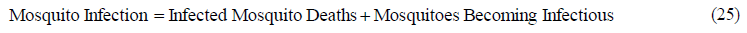
The exposed mosquito deaths are equal to the stock ME divided by the life expectancy of exposed mosquitoes (TE), and the outflow of mosquitoes becoming infectious is equal to the stock ME divided by the time to develop sporozoites (TP):
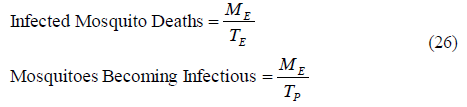
Substituting (22) and (26) in (25), we get the following expression for the human infectivity IH:
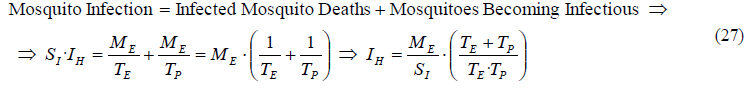
Similarly we can also get the equation for the mosquito infectious rate IR by substituting from (26) the mosquitoes becoming infectious into (24), obtaining the following equation:
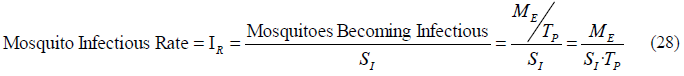
If we divide (27) by (28), and substitute the life expectancy of exposed mosquitoes TE, we can get the relationship between human infectivity IH and mosquito infectious rate IR, depending on the life expectancy of adult mosquitoes TM and the time to develop sporozoites TP:
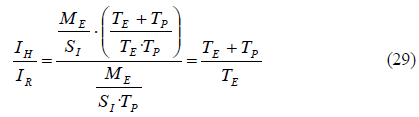
We can observe that the relationship between the two infectivities in (29) does not depend on any prevalence or number of bites. It only depends on mosquito longevities.
Considering that the average life expectancy of adult mosquitoes TM is around three weeks and the time to develop sporozoites TP is not less than 10 days, the human infectivity is around twice the mosquito infectious rate. In that case, only half of the mosquitoes getting infected will become infectious, the rest will die earlier. This is valid for the given values of mosquito life expectancy and extrinsic incubation period. Should those values change due to the implementation of malaria interventions or other factors, we only need to include the new values in the equation (29) in order to obtain the relationship between human infectivity and mosquito infectious rate.
4. Force of Infection, basic reproductive number, and vectorial capacity
In this final chapter, we will calculate the force of infection (FOI), the basic reproductive number (R0), and the vectorial capacity (VC), using a formulation that is related to the structure of the presented model.
-Force of infection (FOI): Also known as infection rate, the FOI is defined as the number of infections per person per unit of time. The FOI counts all incident (that is, new) human malaria infections in some time interval with or without clinical symptoms, and whether or not a person is already infected https [33].
Since we consider all infections, apart from the incidence, we also need to include the re-exposures (reinfections before recovery). The FOI is therefore the result of dividing the sum of incidence and re-exposures by the total population. The incidence and the re-exposures are both included in the following equations, where HI and HS are infected and susceptible humans respectively. We will assume similar mosquito infectivity IM for both groups of people:
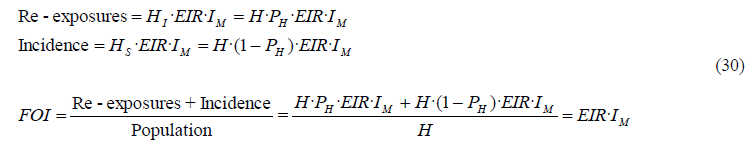
Since units for FOI are annual infections per person and EIR annual infectious bites per person, we observe that the number of infections per infectious bite (FOI/EIR=IM) describes the efficiency of transmission from mosquito to human. If we define the recovery rate for humans as the inverse of the recovery time (1/TR), when the FOI (or infection rate) exactly balances the rate of recovery (IM·EIR = 1/TR), half of the human population is infected:
Taking equation (04) as a reference and substituting the previous equality, we obtain the demonstration:
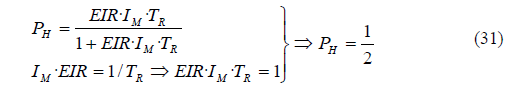
Alternatively, we can also obtain the FOI as the result of dividing the incidence by the susceptible population:
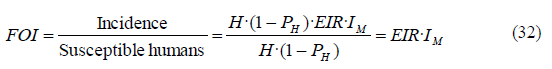
Therefore, the force of infection is a measure of the risk of a susceptible person to become infected per unit time.
- Basic reproductive number (R0): The basic reproduction number R0, is defined as the average number of secondary cases produced by one infected individual introduced into a completely susceptible population. In other words, R0 is the number of infections caused by an infection in an uninfected population https [34]. Since the population will rarely be completely susceptible to an infection in the real world, one way to consider all infections as if they were rising from a totally susceptible population is to include both, infections over infected humans (re-exposures), and infections over susceptible humans (incidence). With this premise, if we divide all the infections (i.e. re-exposures and incidence) by the stock of infected population, we will obtain the average infections per infected person and per unit of time in a totally uninfected population. This is what we call effective contact rate β:
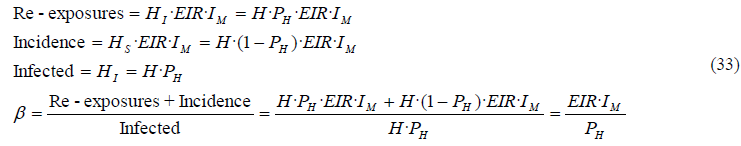
From this equation we can easily deduce that FOI= β·PH. Therefore, the difference between β and FOI is basically that β refers to the infection rate per infected person, while FOI refers to the infection rate per person, regardless of the person’s condition.
Knowing that an average infected person contributes with a number of infections per unit of time, this rate β will continue for as long as the individual is infectious. Therefore, the total number of infections derived from an infected person is the result of multiplying the infections per unit of time β, by the duration of the person’s infectiousness. This duration is considered to be equal to the average recovery time TR. Consequently, the total number of infections per infected person R0 is equal to the individual infections per unit of time β, multiplied by the average duration of the infectiousness TR. We calculate R0 as follows:
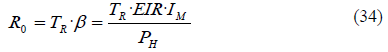
It is important to note that R0 is a dimensionless number and not a rate, which would have 1/time units. R0 can be also expressed as a function of the FOI:
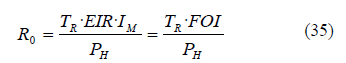
If we only want to calculate the susceptible people who get infected per infected person, we use the effective reproductive number R, where we only consider the incidence or new infections:
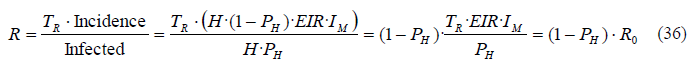
We observe that R is equal to R0 when PH=0, i.e. when all the population is susceptible.
In general, for an epidemic to occur in a susceptible population R0 must be >1, so the number of infected people is increasing. However, R is more appropriate than R0 to verify whether a disease is spreading or not, because it takes into account that not everybody is susceptible.
For example, if R0 is equal to 2 but the prevalence is 60%, the number of new infections per infected person is R=(1-0.6)·2=0.8, which means that for every infected person who gets recovered, there will be 0.8 new infections from the stock of susceptible. Given that in this situation the number of recoveries is bigger than the incidence, the prevalence will decrease over time. Therefore, only when the effective reproductive number R>1 (each infected person contributes with more than one new infection from the susceptible population), the number of infected people or prevalence is increasing.
If R=1, the prevalence is constant, and if R<1, the prevalence will decrease.
In the following equation we demonstrate that R>1 when incidence > recoveries:
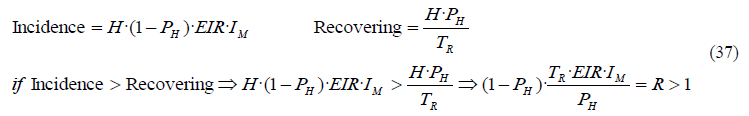
- Vectorial capacity (VC): The vectorial capacity VC is intimately related to the effective contact rate β. It also represents the average number of humans infected per infected human and per unit of time in a completely susceptible human population, but in this case assuming perfect transmission efficiency, i.e. IM = IR = 1.
The reason to assume perfect transmission efficiency is that the VC is a concept that describes the maximum potential of a vector to transmit a pathogen https [35]. Given that in the real world there is not perfect transmission efficiency, we can define VC as the total number of potentially infectious bites that would eventually arise from all the mosquitoes biting a single perfectly infectious (i.e. all mosquito bites result in infection) human on a single day https [36] (Note that all our rates are in annual terms and this definition uses day as time units. In any case, we can convert annual values into daily if we divide them by 365).
Since IM and IR are normally <1, the vectorial capacity VC is bigger than β. Taking equation (33) as a reference, we obtain VC:
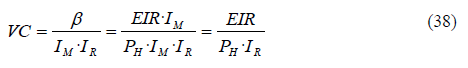
Once we put in transmissibility (IM and IR) and the duration of infectiousness TR, we have a measure directly analogous to R0. Therefore, the basic reproduction number R0 can be also expressed as a function of VC:
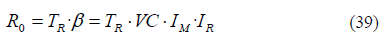
Some authors use an alternative definition for vectorial capacity; the number of infectious bites that would eventually arise from all the mosquitoes that bite a fully infectious human per unit of time [4]. This would be equal to VC, multiplied by the transmission efficiency IR.
5. Discussion
The model presented in this paper aims for a better understanding of the mechanisms involved in malaria transmission. We have started from the simplest model version, and despite the added complexity in the different chapters, these versions are still generic and have some limitations.
During the development of the present model we have already mentioned different limitations. In this regard, the model contains the essential mechanisms of malaria transmission, but is missing other sectors like a mosquito breeding sector, or effects, like the effects of the environment in mosquito development, parasite transmission, etc., which are included in more complex versions of the model. Another limitation is that we have considered the system homogeneous: For most of the indicators, the presented models use average values and do not make differentiations among humans, mosquitoes, or even P. falciparum parasites. In this primary version, we have simplified the model by considering homogeneous mosquito populations or parasite infectivity (ability of sporozoites to invade the liver of the host). Also in line with the mosquitoes, we have not included the possibility of different Anopheles species transmitting malaria with different biting behaviors, and even mosquitoes from the same species do not have the same biting patterns; for example, infectious stage mosquitoes normally increase their motivation to bite, increasing also their share of the total bites and changing their behavioral response against insecticides https [37].
Regarding humans, we have considered all the persons in an area to be similarly attractive to mosquito bites, although for instance, pregnant women can attract more mosquito bites https [38]. Moreover, malaria infection can render humans more attractive to Anopheles mosquitoes than uninfected people https [39], making the infected people to have also a bigger share of the total bites. In fact, evidence suggests that in some locations a core group of the human population receive a substantial proportion of mosquito bites because of proximity to larval habitat or differential attractiveness to mosquitoes (for example, up to 80% of the bites might be taken on just 20% of the population), increasing the level of heterogeneity https [40].
The homogenization of these and other model variables can lead to a certain level of inaccuracy in the results, but yet the models can be close enough to reality and help to understand the malaria transmission in the area of analysis. For more accurate results, the models are flexible to add more complexity, which is strongly subordinate to the ability to find the necessary data that is required. Therefore, most of the limitations can be overcome by adding the necessary level of detail, although the difficulty leans mostly upon finding reliable data. In fact, the quality of the statistical information available regarding malaria in Sub-Saharan regions is usually very poor https [41] https [42].
But even in the absence of some data, sometimes it is possible to extrapolate values from other similar locations, use the literature, or calculate them directly in the model. Nevertheless, the purpose of the model is what in the end will determine the needed level of detail or precision.
In this regard, one of the purposes of malaria models is to design adequate malaria control programs in the areas of study, and one of the most successful ways to plan malaria control policies is through the use of Integrated Vector Management (IVM) [43] https. Since IVM works reducing malaria transmission using different interventions, the models require differentiation between malaria transmission outdoors and indoors. To that extent the model can be enlarged in order to capture the different dynamics between indoor and outdoor mosquitoes.
We do not elaborate mathematically on the impact of IVM interventions in this paper but if we assume the inclusion of indoor and outdoor sectors in the model, we can at least indicate briefly the dynamics of the different interventions in our model: As mentioned before, bed net usage can reduce the indoor vector biting rate. And since the nets restrict the access to indoor blood meals, the mosquitoes will try to find another way to bite hosts, which in return can eventually affect the peak biting hours [44] https, the outdoor biting rate, and also the human blood index [45] https. A decrease in the human blood index would decrease proportionally the annual bites on humans per mosquito BR.
Nowadays most nets are treated (Long Lasting Insecticide-treated Nets, or simply LLINs), and they can therefore contribute to kill some of the mosquitoes. The same applies to IRS (Indoor Residual Spraying), which reduces both, the longevity of indoor mosquitoes and the willingness of mosquitoes in general to get indoors (excito-repellency that reduces the number of indoor mosquitoes per person). We have to consider however, that the efficacy of these methods is highly dependent on the mosquito resistance to the insecticides.
Regarding outdoor interventions, environmental management operations, including source reduction or larviciding [46] https, can reduce the inflow of new adult mosquitoes into the environment, reducing also mosquito density and consequently the number of biting mosquitoes per person. If we assume a constant number of annual bites per mosquito BR, a decrease in the number of biting mosquitoes per person M would reduce proportionally the vector biting rate VR (based on equation (07), where VR=BR·M).
The reduction in mosquito density and bites per person after implementing the different interventions can be obtained empirically. These effects can be included in the model, allowing a holistic assessment of the combined impact from different IVM interventions in reducing malaria transmission.
Should the interventions reduce significantly the incidence, the prevalence and the level of re-exposures would be also reduced. Consequently, the fraction of asymptomatic population would decrease over time, which in turn would decrease also the recovery time (assuming proper case management and prompt treatment). In our case, the recovery time comprises the period for a complete elimination of malaria parasites from the body (we do not use the term “radical cure” as it is only used for P. vivax and P. ovale infections to reflect the use of anti-hypnozoite medicines). Therefore, a decrease in the recovery time implies a shorter infectious period, which reduces the availability of parasites in humans and results in a lower human prevalence.
As a result, a decrease in human prevalence would lead to a reduction in the mosquito infection rate and the consequent reduction in mosquito prevalence, which in turn would lead to a smaller EIR and further reduction in human prevalence. This major feedback loop is represented with red arrows in the figure 10, where we have put together the basic human sector (figure 03) and mosquito sector (figure 07).
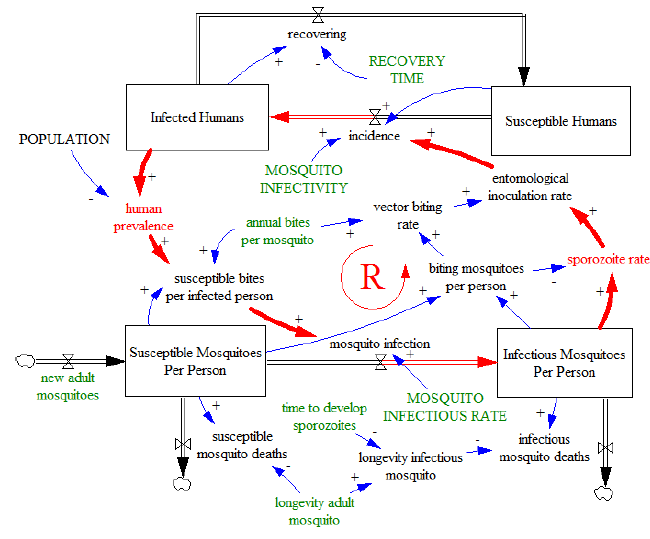
Figure 10
If for example we assume a significant increment in the number of new adult mosquitoes, this disturbance would break the steady state of the system, and the major feedback loop could trigger rapid increases in human prevalence leading to an epidemic situation. On the contrary, if the transmission is compromised by a very low density of humans or mosquitoes carrying the parasite, the loop can develop into malaria elimination. In fact, should the prevalence be reduced under some thresholds, malaria transmission would become unsustainable and be eliminated. In that situation, the obtained equilibrium value for any prevalence in the model would reach marginal values that are in practice equal to zero.
Therefore, this major feedback loop aims to bring the system into extreme situations (PH=1 or PH=0). Given its nature, we define the major feedback loop as reinforcing, in agreement with the System Dynamics theory. The loop is actually symbolized in the figure 10 by a big letter R surrounded by the logo of a circular arrow which indicates the direction of the causality.
The variables colored in green are those that can vary through external factors, playing a fundamental role in defining the behavior of this loop. However, for the purpose of simplicity, we do not represent the effects of the different malaria control interventions that we have mentioned before. Since malaria transmission is also subject to balancing feedbacks, the system needs to include other counteracting loops that prevent the prevalence from reaching extreme values and allow temporal steady states when the forces of the system are in equilibrium. For example, the recovery of humans decreasing the stock of infected humans, or the mosquito deaths decreasing the stock of mosquitoes are part of other balancing loops that impede our major feedback loop from increasing malaria prevalence uncontrolled. Other examples of balancing loops can be found by analyzing the transmission efficiency or infectivity:
For example, several studies that have estimated the mosquito infectivity IM have shown that mosquito-to-human transmission is extremely inefficient in high-intensity settings (high EIR). On the contrary, as malaria prevalence falls, transmission dynamics and immunoepidemiology change and infected mosquitoes are more likely to transmit the infection [33]. Something very similar happens with the human-to-mosquito transmission efficiency IH. In highly endemic areas, a small fraction of mosquitoes biting an infected host develop sporozoites, but as malaria prevalence becomes smaller, the human infectivity increases https [47].
Regardless of the reasons that relate human prevalence with infectivity, there is a causality indicating that a higher prevalence will lead to lower mosquito infectivity. In this case, incidence would become smaller, which in return would reduce prevalence, generating a balancing loop as indicated in figure 11.
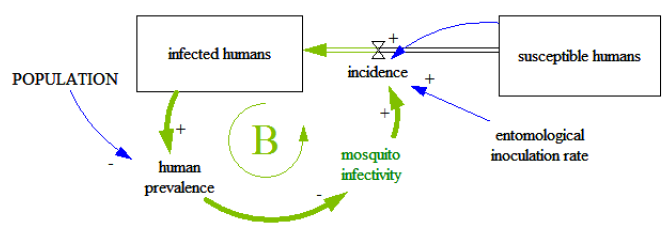
Figure 11
Depending on how much human prevalence affects mosquito infectivity, we can deduce the extent at which this change in transmission efficiency complicates the relationship between human prevalence and the EIR represented in figure 04.
A similar balancing loop is present when dealing with the human infectivity: Higher human prevalence leads to less efficient human-to-mosquito transmission, which in return decreases sporozoite rate, decreasing also incidence and human prevalence. These loops are not represented in the figure 10 but they might need to be included in the models when the prevalence in the area of analysis experiences significant variations. Based on the discussion so far, and in addition to all the static analysis performed under the assumption of temporal steady state, we can conclude that the presented model portrays feedback loops that can develop changes in the behavior of the system, generating different dynamics of malaria transmission. Given that we are dealing with an infectious disease, our dynamic analysis would focus on changes in the incidence or prevalence of the population over time [4].
A last consideration in interpreting our results is about the annual bites on humans per mosquito BR and its significance regarding malaria transmission. As we deduced from (07), any reduction of BR or M would reduce VR, reducing also the EIR. However, similar fractional reduction in BR and in M does not have the same relevance:
If we substitute the vector biting rate (07) and the mosquito prevalence (17) in the equation (01) that defines the EIR, we get the following equation:
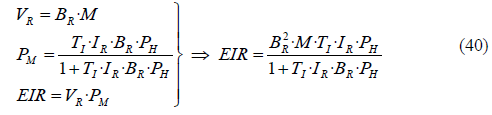
From this equation we already considered in (18) that the term (1+TI·IR·BR·PH) is approximately equal to 1, making possible to simplify (40) by removing the denominator:
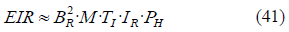
As we indicated, the intensity of malaria transmission is expressed through the EIR, which represents the number of infective bites received by an individual during the year. This number can be obtained in (41) by multiplying different factors, and we observe that BR is raised to the power of 2, which means that the EIR is significantly more sensitive to BR than to any other factor. In fact, variations in M might not have the expected effect in the EIR since, as we suggested previously, increasing M might decrease BR (or reducing M might increase BR), which would partially cancel out the effect of M on the EIR.
To put an example, if we had a constant number of 10 mosquitos per person, and each of them bite a human once per week, the malaria transmission would be less intense than having 5 mosquitoes per person, each of them biting twice per week. It is true that in both cases the total number of mosquito bites is the same, but it is also logical to think that mosquitos with higher biting activity are more likely to contract malaria and therefore transmit it to someone else, which means that for malaria transmission, BR is more critical than the number of mosquitoes per person M.
As a result, reducing BR plays an even more essential role in malaria reduction than reducing the mosquito density. If for example, we reduce the bites per mosquito BR by half, the resulting EIR would be four times smaller.
In this sense, another important factor is the human blood index: Mosquitoes having most of their blood meals from humans contribute to a higher BR that could trigger epidemics even when mosquito density M has been reduced significantly. Therefore, diverting the bites on humans to other animal species can also play an important role in reducing malaria transmission. In order to have an idea of the variations in the average bites per mosquito BR, we can use the expression (21), where BR is approximately proportional to the ratio PM/PH.
6. Conclusion
We have fitted a simple stock and flow model which allows us to understand the most important mechanisms of malaria transmission in P. falciparum carriers. Although the starting model is very simple, the results obtained after increasing the model complexity are very similar.
The mathematical relationships established in the model can help us to obtain or validate the value of the main malaria transmission indicators by eliminating three degrees of freedom. In this sense, one of the most relevant results from this study is the calculated ratio or relationship between mosquito and human prevalence (PM/PH), which is approximately equal to a constant that depends on the entomological and environmental conditions of the area, multiplied by the average bites on humans per mosquito BR. Regarding BR, it can be also calculated using other variables obtained by observation and is particularly relevant for malaria transmission as it would enable high levels of human prevalence even in environments with low mosquito densities.
Although the relationships in the model are obtained from the perspective of a static analysis, the inclusion of data would allow the model to simulate over time and to manifest the behavior of the variables driven by the different feedback loops of the system, thus permitting also dynamic analyses. So far we have developed introductory models that can help us to understand better the problem of malaria transmission. However, we have not used them yet to solve this problem. One of the next steps in this direction would be to introduce different malaria control interventions into the model, making possible to simulate them and observe their outcome over time, which in return would provide a platform from where it is possible to analyze dynamically their impact on malaria transmission. Once validated for specific locations, the models can be used as decision-support tools to improve the design of strategies against malaria in the different areas.
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable
Availability of data and materials
Not applicable
Competing interests
The author declares that he has no competing interests.
Funding
Not applicable
Authors' contributions
Not applicable
Acknowledgements
I would like to thank my supervisor, Prof. Pål I. Davidsen, for providing feedback and advice throughout this project, and for his patient guidance and encouragement. I have been very lucky to have a supervisor who cared so much about my work.
References
- Autino B, et al., Epidemiology of malaria in endemic areas. Mediterranean journal of hematology and infectious diseases 4 (2012): e2012060-e2012060.
- Rosenthal PJ. How do we best diagnose malaria in Africa? Am J Trop Med Hyg 86 (2012): p. 192-3.
- White NJ. Determinants of relapse periodicity in Plasmodium vivax malaria. Malar J 10 (2011): p. 297.
- Smith DL and McKenzie FE. Statics and dynamics of malaria infection in Anopheles mosquitoes. Malar J 3 (2004): p. 13.
- Homer JB and Hirsch GB. System dynamics modeling for public health: background and opportunities. Am J Public Health 96 (2006): p. 452-8.
- Koella JC. On the use of mathematical models of malaria transmission. Acta Tropica 49 (1991): p. 1-25.
- WHO, WHO malaria terminology (2018).
- Kilama M, et al. Estimating the annual entomological inoculation rate for Plasmodium falciparum transmitted by Anopheles gambiae s.l. using three sampling methods in three sites in Uganda. Malar J 13 (2014): p. 111.
- Kabbale F, et al. Biting times of Plasmodium falciparum infected mosquitoes and transmission intensities following five years of insecticide-Treated bed nets use in Kamuli District, Uganda: Implications for malaria control. International Journal of Mosquito Research 3 (2016).
- Beier J, Killeen G, and Githure JI. Short report: Entomologic inoculation rates and Plasmodium falciparum malaria prevalence in Africa 61 (1999): 109-13.
- Churcher TS, et al. Probability of Transmission of Malaria from Mosquito to Human Is Regulated by Mosquito Parasite Density in Naive and Vaccinated Hosts. PLoS Pathog 13 (2017): p. e1006108.
- Lindblade KA, et al. The silent threat: asymptomatic parasitemia and malaria transmission. Expert Rev Anti Infect Ther 11 (2013): p. 623-39.
- Felger I, et al. The dynamics of natural Plasmodium falciparum infections. PLoS One 7 (2012): p. e45542.
- Birley MH and Charlewood JD. Sporozoite rate and malaria prevalence. Parasitol Today 3 (1987): p. 231-2.
- Ndoen E et al. Mosquito Longevity, Vector Capacity, and Malaria Incidence in West Timor and Central Java, Indonesia. ISRN Public Health (2012): p. 1-5.
- Charlwood JD, et al. Feeding frequency and survival of Anopheles gambiae in a rice-growing area in Ghana. Med Vet Entomol 26 (2012): p. 263-70.
- Ndiath MO, et al. Methods to collect Anopheles mosquitoes and evaluate malaria transmission: a comparative study in two villages in Senegal. Malar J 10 (2011): p. 270.
- Beier JC, Malaria parasite development in mosquitoes. Annu Rev Entomol 43 (1998): p. 519-43.
- Klowden MJ, Blood, Sex, and the Mosquito. BioScience 45 (1995): p. 326-331.
- Graves PM, et al. Measurement of malarial infectivity of human populations to mosquitoes in the Madang area, Papua New Guinea. Parasitology 96 (2009).
- Gardiner DL and Trenholme KR. Plasmodium falciparum gametocytes: playing hide and seek. Annals of translational medicine 3 (2015): p. 45-45.
- Githeko AK, et al, The reservoir of Plasmodium falciparum malaria in a holoendemic area of western Kenya. Trans R Soc Trop Med Hyg 86 (1992): p. 355-8.
- Ashley EA and White NJ. The duration of Plasmodium falciparum infections. Malar J 13 (2014): p. 500.
- Azikiwe CCA, et al. A comparative laboratory diagnosis of malaria: microscopy versus rapid diagnostic test kits. Asian Pacific Journal of Tropical Biomedicine 2 (2012): p. 307-310.
- Dalrymple U, et al. How long do rapid diagnostic tests remain positive after anti-malarial treatment? Malar J 17 (2018): p. 228.
- Nosten F and White NJ. Artemisinin-Based Combination Treatment of falciparum Malaria 77 (2008): 181-92.
- Wilairatana P, Krudsood S, and Tangpukdee N. Appropriate time for primaquine treatment to reduce Plasmodium falciparum transmission in hypoendemic areas Korean J Parasitol 48 (2010): p. 179-82.
- Mueller I, et al. The sensitivity of the OptiMAL rapid diagnostic test to the presence of Plasmodium falciparum gametocytes compromises its ability to monitor treatment outcomes in an area of Papua New Guinea in which malaria is endemic. J Clin Microbiol 45 (2007): p. 627-30.
- Bousema T, et al. Revisiting the circulation time of Plasmodium falciparum gametocytes: molecular detection methods to estimate the duration of gametocyte carriage and the effect of gametocytocidal drugs. Malar J 9 (2010): p. 136.
- Arévalo-Herrera M, et al. Malaria transmission blocking immunity and sexual stage vaccines for interrupting malaria transmission in Latin America. Memórias do Instituto Oswaldo Cruz 106 (2011): p. 202-211.
- Doolan DL, Dobano C and Baird JK. Acquired immunity to malaria. Clin Microbiol Rev 22 (2009): p. 13-36.
- Beier JC, et al. Integrated vector management for malaria control. Malar J 7 (2008): p. S4.
- Smith DL, et al. A quantitative analysis of transmission efficiency versus intensity for malaria. Nat Commun 1 (2010): p. 108.
- van den Driessche P. Reproduction numbers of infectious disease models. Infect Dis Model 2 (2017): p. 288-303.
- Catano-Lopez A, et al. An alternative model to explain the vectorial capacity using as example Aedes aegypti case in dengue transmission. Heliyon 5 (2019): p. e02577.
- Brady OJ, et al. Vectorial capacity and vector control: reconsidering sensitivity to parameters for malaria elimination. Trans R Soc Trop Med Hyg 110 (2016): p. 107-17.
- Thievent K, et al. Malaria infection in mosquitoes decreases the personal protection offered by permethrin-treated bednets. Parasit Vectors 11 (2018): p. 284.
- Himeidan YE, Elbashir MI and Adam I. Attractiveness of pregnant women to the malaria vector, Anopheles arabiensis, in Sudan. Ann Trop Med Parasitol 98 (2004): p. 631-3.
- Emami SN, et al. A key malaria metabolite modulates vector blood seeking, feeding, and susceptibility to infection. Science 355 (2017): p. 1076-1080.
- Smith DL, et al. The entomological inoculation rate and Plasmodium falciparum infection in African children. Nature 438 (2005): p. 492-5.
- Ohiri K, et al. An Assessment of Data Availability, Quality, and Use in Malaria Program Decision Making in Nigeria. Health Systems & Reform 2 (2016): p. 319-330.
- Chilundo B, Sundby J and Aanestad M. Analysing the quality of routine malaria data in Mozambique Malar J 3 (2004): p. 3.
- Tizifa TA, et al. Prevention Efforts for Malaria. Curr Trop Med Rep 5 (2018): p. 41-50.
- Yohannes M and Boelee E. Early biting rhythm in the Afro-tropical vector of malaria, Anopheles arabiensis, and challenges for its control in Ethiopia. Med Vet Entomol 26 (2012): p. 103-5.
- Killeen GF. Characterizing, controlling and eliminating residual malaria transmission. Malar J 13 (2014): p. 330.
- Malaria control: the power of integrated action.
- Churcher TS, Trape JF and Cohuet A. Human-to-mosquito transmission efficiency increases as malaria is controlled. Nat Commun 6 (2015): p. 6054.


 Impact Factor: * 6.2
Impact Factor: * 6.2 Acceptance Rate: 76.33%
Acceptance Rate: 76.33%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 