Comparison of Stress In Peri-Implant Bone of Anterior Maxilla on Loading of Straight and Angulated Platform Switched Implant Abutments - A 3D Finite Element Analysis
Shashank Vijapure1, Nisha Singh2, Vikender Singh Yadav3, Shailesh Kumar4*, Kamini Kiran5
1Private Practitioner, Department of Periodontics, Faculty of Dental Sciences, M S Ramaiah University of Applied Sciences, Bangalore, India
2Division of Periodontics, Centre for Dental Education and Research, All India Institute of Medical Sciences, New Delhi, India, India
3Division of Periodontics, Centre for Dental Education and Research, All India Institute of Medical Sciences, New Delhi, India
4Department of Dentistry, All India Institute of Medical Sciences, Rishikesh, India
5Department of Pathology, All India Institute of Medical Sciences, Rishikesh, India
*Corresponding Author: Shailesh Kumar, Department of Dentistry, All India Institute of Medical Sciences, Rishikesh, India.
Received: 05 September 2019; Accepted: 30 October 2019; Published: 06 January 2020
Article Information
Citation: Shashank Vijapure, Nisha Singh, Vikender Singh Yadav, Shailesh Kumar, Kamini Kiran. Comparison of Stress In Peri-Implant Bone of Anterior Maxilla on Loading of Straight and Angulated Platform Switched Implant Abutments - A 3D Finite Element Analysis. Archives of Clinical and Medical Case Reports 4 (2020): 030-043.
View / Download Pdf Share at FacebookAbstract
Background: Literature have shown the microbiological and mechanical benefits gained from using platform switching. Also there is increasing need for intentional inclination of the implants in specific situations like those placed in the anterior maxilla. There are no studies that evaluate the bone behaviour when using abutments associated with the principle of platform switching in different angulations in anterior maxilla. The aim of the present study was to measure and compare the stress distribution on peri-implant bone when implants are placed in the anterior maxilla using 2 different abutments with different angulations and 2 different load conditions, by means of 3D-Finite Element Analysis (FEA) which might be a powerful and effective tool to visualize such a situation.
Materials and Methods: Six mathematical models of implant-supported central incisor were created with varying abutment angulations: straight abutment (S1 and S2), angulated abutment at 15 degrees (A1 and A2) and angulated abutment at 20 degrees (A3 & A4), submitted to 2 loading conditions (146 N): S1, A1 and A3 oblique loading (45 degrees) and S2, A2 and A4 axial loading, parallel to the long axis of the implant. Maximum (Rmax) and minimum (Rmin) principal stress values were obtained for cortical and trabecular bone.
Results: All models showed higher stress on the peri-implant bone when subjected to oblique loading. For the cortical bone, the maximum principal stress (σ max) was highest in A1(45.53) followed by S1(34.82), A2(30.31), A3(24.85), S2(19.69) MPa and the least being in A4(16.57). For the trabecular bone, the σ max was highest in S1(8.75), followed by A1(12.12), S1(8.75), A2(7.12), A3(6.18), A4(4.12), and in S2(3.28) being the least.
Conclusion: Implants demonstrated increased maximum principal stress in oblique loading compared to axial loading in all the models. Maxi
Keywords
Platform switching implant; 3D-FEA; Bone; Stress distribution; Angulated abutment
Platform switching implant articles, 3D-FEA articles, Bone articles, Stress distribution articles, Angulated abutment articles
Platform switching implant articles Platform switching implant Research articles Platform switching implant review articles Platform switching implant PubMed articles Platform switching implant PubMed Central articles Platform switching implant 2023 articles Platform switching implant 2024 articles Platform switching implant Scopus articles Platform switching implant impact factor journals Platform switching implant Scopus journals Platform switching implant PubMed journals Platform switching implant medical journals Platform switching implant free journals Platform switching implant best journals Platform switching implant top journals Platform switching implant free medical journals Platform switching implant famous journals Platform switching implant Google Scholar indexed journals 3D-FEA articles 3D-FEA Research articles 3D-FEA review articles 3D-FEA PubMed articles 3D-FEA PubMed Central articles 3D-FEA 2023 articles 3D-FEA 2024 articles 3D-FEA Scopus articles 3D-FEA impact factor journals 3D-FEA Scopus journals 3D-FEA PubMed journals 3D-FEA medical journals 3D-FEA free journals 3D-FEA best journals 3D-FEA top journals 3D-FEA free medical journals 3D-FEA famous journals 3D-FEA Google Scholar indexed journals Bone articles Bone Research articles Bone review articles Bone PubMed articles Bone PubMed Central articles Bone 2023 articles Bone 2024 articles Bone Scopus articles Bone impact factor journals Bone Scopus journals Bone PubMed journals Bone medical journals Bone free journals Bone best journals Bone top journals Bone free medical journals Bone famous journals Bone Google Scholar indexed journals Stress distribution articles Stress distribution Research articles Stress distribution review articles Stress distribution PubMed articles Stress distribution PubMed Central articles Stress distribution 2023 articles Stress distribution 2024 articles Stress distribution Scopus articles Stress distribution impact factor journals Stress distribution Scopus journals Stress distribution PubMed journals Stress distribution medical journals Stress distribution free journals Stress distribution best journals Stress distribution top journals Stress distribution free medical journals Stress distribution famous journals Stress distribution Google Scholar indexed journals Surgeon articles Surgeon Research articles Surgeon review articles Surgeon PubMed articles Surgeon PubMed Central articles Surgeon 2023 articles Surgeon 2024 articles Surgeon Scopus articles Surgeon impact factor journals Surgeon Scopus journals Surgeon PubMed journals Surgeon medical journals Surgeon free journals Surgeon best journals Surgeon top journals Surgeon free medical journals Surgeon famous journals Surgeon Google Scholar indexed journals treatment articles treatment Research articles treatment review articles treatment PubMed articles treatment PubMed Central articles treatment 2023 articles treatment 2024 articles treatment Scopus articles treatment impact factor journals treatment Scopus journals treatment PubMed journals treatment medical journals treatment free journals treatment best journals treatment top journals treatment free medical journals treatment famous journals treatment Google Scholar indexed journals Dental articles Dental Research articles Dental review articles Dental PubMed articles Dental PubMed Central articles Dental 2023 articles Dental 2024 articles Dental Scopus articles Dental impact factor journals Dental Scopus journals Dental PubMed journals Dental medical journals Dental free journals Dental best journals Dental top journals Dental free medical journals Dental famous journals Dental Google Scholar indexed journals pregnancy articles pregnancy Research articles pregnancy review articles pregnancy PubMed articles pregnancy PubMed Central articles pregnancy 2023 articles pregnancy 2024 articles pregnancy Scopus articles pregnancy impact factor journals pregnancy Scopus journals pregnancy PubMed journals pregnancy medical journals pregnancy free journals pregnancy best journals pregnancy top journals pregnancy free medical journals pregnancy famous journals pregnancy Google Scholar indexed journals FEA articles FEA Research articles FEA review articles FEA PubMed articles FEA PubMed Central articles FEA 2023 articles FEA 2024 articles FEA Scopus articles FEA impact factor journals FEA Scopus journals FEA PubMed journals FEA medical journals FEA free journals FEA best journals FEA top journals FEA free medical journals FEA famous journals FEA Google Scholar indexed journals Borchers articles Borchers Research articles Borchers review articles Borchers PubMed articles Borchers PubMed Central articles Borchers 2023 articles Borchers 2024 articles Borchers Scopus articles Borchers impact factor journals Borchers Scopus journals Borchers PubMed journals Borchers medical journals Borchers free journals Borchers best journals Borchers top journals Borchers free medical journals Borchers famous journals Borchers Google Scholar indexed journals
Article Details
1. Introduction
Dental implants have been undoubtedly one among the most significant scientific breakthroughs of the dental field in the past 30 years [1]. A key factor for the success or failure of a dental implant is the manner in which stresses are transferred to the surrounding bone. In the past 2 decades, Finite element analysis (FEA) has become an increasingly useful tool for the prediction of the effects of stress on the implant and its surrounding bone. FEA is a technique for obtaining a solution to a complex mechanical problem by dividing the problem domain into a collection of much smaller and simpler domains (elements) in which the field variables can be interpolated with the use of shape functions. Because the components in a dental implant-bone system are extremely complex geometrically, FEA has been viewed as the most suitable tool for analyzing them. FEA was initially developed in the early 1960s to solve structural problems in the aerospace industry, but has since been extended to solve problems in heat transfer, fluid flow, mass transport, and electromagnetics. In 1976, Weinstein et al. [2] were the first to use FEA in implant dentistry; subsequently, FEA was applied rapidly in that field. Atmaram and Mohamed [3-5] analyzed the stress distribution in a single-tooth implant to understand the effect of elastic parameters and geometry of the implant, implant length variation, and pseudo-periodontal ligament incorporation. Borchers and Reichart [6] performed a 3-dimensional FEA of an implant at different stages of bone interface development.
Several studies [7-12] published in the literature have shown the benefits gained from using platform switching, a concept based on the use of an implant with a larger diameter than the abutment diameter. This configuration has been related to microbiological and mechanical benefits, such as reducing inflammatory cell infiltration at the implant-abutment interface and diminished stress on the periimplant bone in comparison with the conventional system [13, 14]. When more intense bone resorption occurs, this may impair aesthetics and the soft tissue architecture [15, 16]. Moreover, bone loss usually begins in the crestal area of the cortical bone and can progress toward the apical region, jeopardizing the longevity of the implant and prosthesis [17]. It is suggested that optimization of an implant may favor the mechanical environment for the maintenance of bone [18].
The need for intentional inclination of the implants should also be considered in specific situations, especially in cases in which dental implants are placed to support restorations in the anterior maxilla. Here, aesthetic or spatial needs arising from the limited available bone anatomy may require the use of abutments to allow proper positioning of the prosthesis, without causing functional or cosmetic damage [19, 20].
Few investigators have studied the unavoidable situation of placing and loading implants at angulations in the anterior maxilla [20], there are no studies that evaluate the bone behaviour when using abutments associated with the principle of platform switching in different angulations based on surgical-driven approaches and their comparison with platform switched straight abutments.
Therefore, the need of the current study is to measure and compare the stress distribution on peri-implant bone when implants are placed in the anterior maxilla using 2 different abutments with different angulations and 2 different load conditions, by means of 3D-Finite Element Analysis (FEA) which might be a powerful and effective tool to visualize such a situation [21-37].
2. Materials and Methods
The study was conducted in the Department of Periodontics, M.S. Ramaiah Dental College, Bangalore, with technical assistance from M S Ramaiah School of Advanced Studies, Bangalore. A cone beam computed tomography (CBCT) scan of a fully dentate maxilla was retrieved from the database of the M S Ramaiah Dental College & Hospital.
The criteria for selection was, a scan with lack of metallic restorations in the region, to limit radiographic artifacts. Data from the CBCT scans were used to build 3-dimensional patient-specific models of the anterior maxilla. Which were obtained in DICOM format. The radiographic density in the CBCT scans was used to assign individual mechanical parameters to each element in terms of Hounsfield units (HU). A value of 0 HU was defined as the radiodensity of distilled water at standard temperature and pressure, and the raiodensity of air at standard temperature and pressure was –1000 HU. Data Acquisition Preoperative data for the patient were acquired with a CBCT scanner (CS 9300, Carestream Health, Inc., 2012) with 0.3-mm voxel resolution, which was designed especially for dental and maxillofacial applications. CBCT scan of Implants were taken mounting the implants on wax block. Both the implants were mounted in identical position, for standardisation. The implant models too were imported into Mimics software (Materialise) and positioned in the anterior segment of the maxilla corresponding to the region of the left central incisor at different angulations, in different mathematical models. After the implants were placed in the proper position, the abutment screw model were imported and aligned with the respective implants, as per the desired conditions for the study. Two types of meshes, a surface mesh and a volumetric mesh were necessary, to produce the FEA model. Converted CBCT data were imported to a visualization program called Mimics (Materialise, Leuven, Belgium) to generate an outline of the maxilla, which resulted in a smooth-surface triangle mesh that was ready for further processing.

Figure 1: Models of anterior maxilla with placement of angulated implants.
Figure 2: Different parts of model after meshing.

Figure 3: Trabecular bone model after meshing.

Figure 4: Straight and angulated abutments with implants after meshing. Total number of nodes=23785, Total number of elements=126735, 4-noded tetrahedral elements used.
Total of Six mathematical models representing the anterior segment of the maxilla were fabricated using software programs. These model Implants with ceramic crowns cemented on the abutments with a 0.05-mm-thick layer of cement were as follows:
In 2 models, the placement of a straight abutment (S1 and S2) were simulated, in 2 models (A1 and A2), the abutments were angulated at 15 degrees, whereas in the other 2 models (A3 and A4), the abutments were angulated at 20 degrees. All The 6 models were subjected to the same loading force 146 N load applied 3 mm below the incisal edge on the palatal surface of the simulated crown,
Under 2 different conditions:
1) S1, A1and A3 → force applied in the oblique direction, at 45 degrees to the long axis of the implant
2) S2, A2 and A4 → axial force, applied parallel to the long axis of the implant.
The fixed support was determined along the 3 Cartesian axes (x = y = z = 0) to characterize the boundary condition. (world beyond the stopping point, i.e. Everything else, that have not been modelled).
3. Results
All models showed higher stress on the peri-implant bone when subjected to oblique loading. For the cortical bone, the Maximum Principal Stress (σ max) was highest in A1 followed by S1, A2, A3, S2 and the least being in A4. (Table 1). For the trabecular bone, the σ max was highest in S1, followed by A1, S1, A2, A3, A4, and in S2 being the least (Table 1). Oblique force generated an increase of 50-77 % in the maximum principal stress in the cortical bone. The stress, increased by approximately by 77% in Straight abutments (S2). Whereas, It increased by 50% with the application of oblique load (force at an angle of 45 degrees to the long axis of the crown) in 150 (A2) & 200 Angulated Abutments (A4). In the trabecular bone the stress increased by approximately 1.5 to 2.5 times, and maximum stress increment was seen in Straight Abutment (Graph 1.)
When the behaviour of the different abutments was analysed in cortical bone, an increase of 30% σ max was observed in the case of the oblique load, when the 150 Angulated abutment (A1) was used compared to the straight abutment (S1), wherein a decrease of load by 30% was seen in case of 200 Angulated abutment (A3). Also, when the load was applied in the axial direction (A2), the 15o Angulated abutment had a maximum principal stress value approximately 54% higher than that observed in Straight abutment (S2) which decreased by to 15% with 200 Angulated Abutment.
In trabecular bone, load in oblique direction increased peri-implant stress upto 39% in case of 15o Angulated abutment and decreased by 30% in case of 200 Angulated Abutment. Axial loading increased the stress around 15o Angulated abutment by twice that of the peri-implant bone around a Straight implant & a 25% increase was noted in case of 200 Angulated Abutment. Maximum von Mises stress demonstrated almost similar increase in oblique loading as compared to axial loading which was by 50% in cortical bone in all the models. Highest Maximum von Mises stress increment was seen in obliquely loaded straight abutment (S1) (Graph2) which was upto 2.5 times increased compared to axially loaded straight abutment (S2). Also there was an increased von Mises stress in cortical bone with angulated implant abutments ranging from 44- 66% compared to straight implant abutments (S1, S2). Upto 48% increased stress in 150 Angulated abutment (A1, A2) &upto 66% in 200 Angulated Abutment (A3, A4).
A pattern was observed with the models, there was shift of maximum principal stress from the labial to the palatal aspect with angulated abutments when compared to the straight implant abutments, in these platform switched implants (Table 2). Minimum principal stress values are almost same in Trabecular Bone, whereas in cortical bone more stress in S1, S2 was demonstrated that A2, A4, S2, A1, A3 (Graph 3).
|
|
Maximum Principal Stress |
Minimum Principal Stress |
Max. von Mises Stress |
|||
|
Implant types-Load direction |
Cortical |
Trabecular |
Cortical |
Trabecular |
Cortical |
Trabecular |
|
S1 (Straight Oblique Load) |
34.82 |
8.75 |
-15.55 |
-2.69 |
33.92 |
13.09 |
|
S2 (Straight Axial Load) |
19.69 |
3.28 |
-19.74 |
-1.2 |
22.62 |
4.85 |
|
A1 (15 degree Angulated Oblique Load) |
45.53 |
12.12 |
-30.68 |
-1.42 |
50.21 |
6.47 |
|
A2 (15 degree Angulated Axial Load) |
30.31 |
7.12 |
-19.92 |
-0.72 |
32.62 |
4.96 |
|
A3 (20 degree Angulated Oblique Load) |
24.85 |
6.18 |
-37.38 |
-2.58 |
56.25 |
7.57 |
|
A4 (20 degree Angulated Axial Load) |
16.57 |
4.12 |
-24.92 |
-1.72 |
37.5 |
5.05 |
Table 1: Stress Values in peri implant bone (MPa) after loading at 146 N.
|
Maximum Principal Stress Distribution |
||
|
Implant types-Load direction |
Cortical |
Trabecular |
|
S1 (Straight Oblique Load) |
Crestal Palatally |
Labially |
|
S2 (Straight Axial Load) |
Palatally |
Labially |
|
A1(15 degree Angulated Oblique Load) |
Crestal Palatally |
Palatally |
|
A2(15 degree Angulated Axial Load) |
Crestal Labially |
Palatally |
|
A3(20 degree Angulated Oblique Load) |
Crestal Labially |
Palatally |
|
A4(20 degree Angulated Axial Load) |
Crestal Labially |
Palatally |
Table 2: Stress Distribution in the Peri-implant bone (*Crestal is suggestive of the Bone Implant interface).
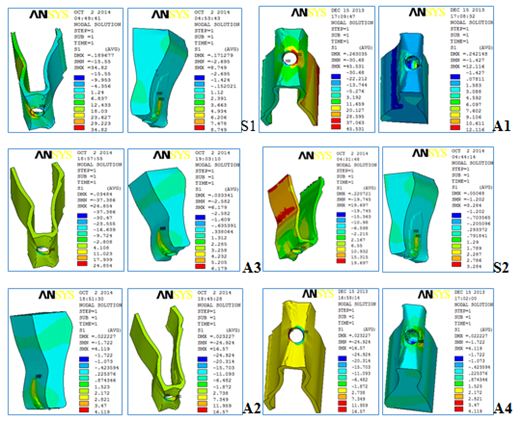
Figure 5: Models representing the anterior segment of the maxilla.
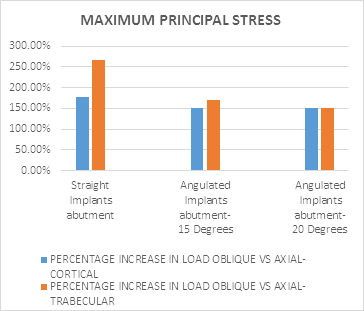
Graph 1: The trabecular bone stress maximum increment.
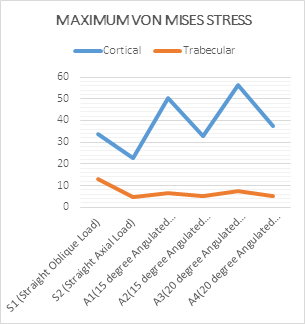
Graph 2: Highest Maximum von Mises stress increment was seen in obliquely loaded straight abutment
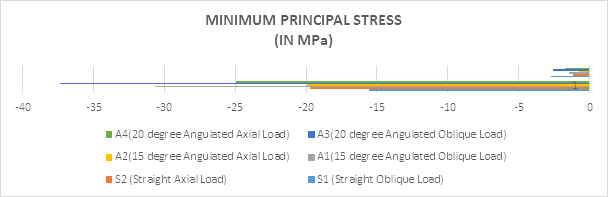
Figure 6: The minimum principal stress values.
4. Discussion
This study was performed to demonstrate the stress generated in peri-implant bone using different abutment angulations of platform switched implants in anterior maxilla. The load applied were obliquely at 450 angulation to the long axis of tooth & parallel to the long axis of tooth. The Oblique load resulted in higher maximum principal stress values in all the models. This was in accordance with several studies performed previously [38-40].
According to Ferrario et al. [41] a 146 N load exerted to the central incisor represents the maximum anterior bite force. The oblique loading with 450 angulation at a point 3 mm apical to the incisal edge on the palatal surface of the simulated crown depicts natural biting force by the mandibular counterpart [42] whereas axial loading simulates a clinical situation in which the incisors are in edge-to-edge position.
In the present study, in an attempt to simulate the natural dentition, loads of 146 N were applied at the above mentioned points, which was the first of its kind study performed in platform switched angulated abutments. The present study demonstrated that, the Maximum Principal Stress (σ max) was highest in A1 (150 angulated abutment) followed by S1, A2, A3, S2 and the least being in A4. An increase in stress was seen from 34.81 MPa in Straight abutment (S1) i.e. 0o to 45.53 MPa in Angulated abutment-15o (A1) However, it was decreased in Angulated abutment-20o (A3) to 24.85 MPa.
Series of similar Studies conducted by Clelland [43-45] regarding angled abutments in which photoelastic, strain gauge, and finite element techniques were employed to study the effect of stress transfer. Their findings suggested that the stresses measured from strain gauge readings for 15-degree and 20-degree abutments were 170% and 190% [45] respectively, compared to the stresses for a 0-degree abutment. Under a similar loading condition but with different material properties for bone and implant, the finite element study [43], revealed only an 11% increase in stress when the abutment angulation was increased from 0 to 20 degrees.
In another study Brosh et al [46], attached strain gauges to implant surfaces and embedded these implants in photoelastic acrylic resins to investigate stress transfer from angled abutments. When the color fringe change within the photoelastic acrylic resin was observed, only an 11% increase in stress was detected when the abutment angulation was increased from 0 to 25 degrees [46]. In the same study, however, the strain-gauge data showed that for 15- and 25-degree abutments, respectively, the increase of strain were 3 and 4.4 times greater, respectively, than the control (0 degrees). Identical results were seen in the present study which can be broadly supported in two ways – First & foremost, influence of variety of factors such as loading condition (magnitude and direction), material properties, and location of strain gauge itself. Secondly, the decrease in maximum stress can be substantiated by the stress distribution. wherein, 15o angulated abutment has shown distribution only palatally, 25o angulated abutment demonstrated both labially and palatally.
In the present study, Oblique loading has shown 77 % increment in principal stress when compared to axial loading in case of straight abutments. In a similar study by Martini et al. [39] the results showed the increased stress values found in models and reinforced the negative effects of oblique force application, also claimed to be similar to those found in the three-dimensional finite element Study of Caglar et al. [47].
Studies of cancellous bone, however, are still insufficient, and in clinical settings, intraoperative examination is still being performed according to the classification of Lekholm and Zarb. Cancellous bone plays an important biomechanical role during load-bearing in peri-implant bone, the mechanism by which the different structures of cortical and cancellous bone affect stress levels and their interaction remain unclear. In the trabecular bone, the stress increased by approximately 1.5 to 2.5 times, and maximum stress increment was seen in Straight Abutment.
In the present study, maximum von Mises stress demonstrated almost similar increase in oblique loading as compared to axial loading which was by 50% in cortical bone in all the models. In a similar study it was found in range (6.48 to 24.51 MPa) of cortical von Mises stress, may be slightly higher than in the in-vivo condition [48].
The values and distributions of (Max. Von mises stress) EQV strain in the bone were similar for both the platform-switched and the matching-diameter abutments in a similar FEA [49]. In addition no significant contribution was found for it in the statistical analysis. These results are in contrast to the findings previously reported by Maeda et al. [7], and the results of the present study.
However, in present study the von Mises stress ranged from 2.5 to 8 times in cortical bone that of σvM in trabecular bone, which was in accordance with a study by Gurgel-Juarez et al. which demonstrated 6 to 14 times higher von Mises stress than that in trabecular bone in all models. Also it was in accordance with the findings of Okumura et al. [49]. For analysis of the results, the maximum principal stress values were obtained for the cortical and trabecular bones. According to Dejak and Mlotkows [50] these analysis criteria are appropriate for predicting failures in nonductile materials.
According to Bayraktar et al. [51] the cortical yield strength, in tension conditions, is 104 MPa. On the other hand, trabecular yield strength, in tension is 82 MPa. The yield strength values are considered as a threshold for microcrack formation in cortical layer of bone. Evidence shows that microcracks stimulate bone remodeling, which begins with bone resorption and is followed by bone formation.
In the present study, even after the platform switched implants were loaded with maximum possible load exerted by the mandibular counterparts on the central incisor teeth.i.e. a load of 146 N. The results demonstrated the maximum principal stress of 45.53 & 12.12 MPa which were well within the yield strength of cortical and trabecular bone respectively, irrespective of the implants placed in any angulation ranging from 0-20 degrees.
It also eliminated the possibilities of any confusion due to application of the physiologic static load range (4.5–9 MPa), which in most studies has led to confusions. On the other hand, the lowest obtained principal stress have been seen to be more (16.57 MPa) in cortical bone and (3.28 MPa) in trabecular bone than the stress magnitudes associated with reduced bone density. The stress magnitudes were studied by the mathematical models for simulating the bone remodeling process under mechanical stimulus [52] and the behaviour of adaptive bone-remodeling simulation models [53], where stress magnitudes of 0 to 2 MPa (under- load) are associated with reduced bone density & stress magnitudes of 4 to 9 MPa are associated with increased bone density, which substantiates the Bio-Mechanical aspect of platform switched implants.
5. Conclusion
This was the first time when a study was designed in an attempt to simulate the natural bite & edge to edge bite under maximum bite force recorded by anteriors. i.e. 146 N on platform switched implant abutments. The results demonstrated increased stress in oblique loading compared to axial loading in all the models. Also increased stress was seen in 150 angulated implants compared to straight implants which reduced on increasing the abutment angulation to 200.
However, the results of the present study should be interpreted with some care. Other scenarios of platform switching, such as different amounts of abutment mismatch, platform switching with a different size of implant shoulder, platform switching in different implant-abutment connections, and platform switching in multiple implant protocols, could also affect the biomechanical environment of implants and should also be investigated. Further, longitudinal clinical studies like experimental studies using strain gauges are necessary to provide more accurate analysis for better implant results.
Conflict of Interest Statement
No conflict of interest
Authors Contribution Statement
- Concept, design, clinical work of the study was done by Dr. Shashank Vijapure
- Drafting of article was look after by Dr Nisha Singh
- Critical revision of article and approval of article was done by Dr Vikender Singh Yadav
- Critical revision and submission of article was done by Dr Shailesh Kumar
- Data management was done by Dr. Kamini Kiran.
References
- Esposito M, Grusovin MG, Maghaireh H, et al. Interventions for replacing missing teeth: different times for loading dental implants. Cochrane Database of Systematic Reviews 3 (2013): CD003878.
- Weinstein AM, Klawitter JJ, Anand SC, et al. Stress analysis of porous rooted dental implants. J Dent Res 55 (1976): 772-777.
- Atmaram GH, Mohammed H. Stress analysis of single-tooth implants. I. Effect of elastic parameters and geometry of implant. Implantologist 3 (1983): 24-29.
- Atmaram GH, Mohammed H. Stress analysis of single-tooth implants. II. Effect of implant root-length variation and pseudo periodontal ligament incorporation. Implantologist 84 (1983): V58-62.
- Mohammed H, Atmaram GH, Schoen FJ. Dental implant design: a critical review. J Oral Implantol 8 (1979): 393-410.
- Borchers L, Reichart P. Three-dimensional stress distribution around a dental implant at different stages of interface development. J Dent Res 62 (1983): 155-159.
- Maeda Y, Miura J, Taki I, et al. Biomechanical analysis on platform switching: is there any biomechanical rationale? Clin Oral Implants Res 18 (2007): 581-584.
- Calvo-Guirado JL, Ortiz-Ruiz AJ, Lo´pez-Mar?´ L, et al. Int J Oral Maxillofac Implants 24 (2009): 275-281.
- Hsu JT, Fuh LJ, Lin DJ, et al. Bone strain and interfacial sliding analyses of platform switching and implant diameter on an immediately loaded implant: experimental and three-dimensional finite element analyses. J Periodontol 80 (2009): 1125-1132.
- Cimen H, Yengin E. Analyzing the effects of the platform switching procedure on stresses in the bone and implant-abutment complex by FEM analysis. J Oral Implantol 38 (2012): 21-26.
- Atieh MA, Ibrahim HM, Atieh AH. Platform switching for marginal bone preservation around dental implants: a systematic review and meta-analysis. J Periodontol 81 (2010): 1350-1366.
- Fickl S, Zuhr O, Stein JM, et al. Peri-implant bone level around implants with platform-switched abutments. Int J Oral Maxillofac Implants 25 (2010): 577-581.
- Cappiello M, Luongo R, Di lorio D, et al. Evaluation of peri-implant bone loss around platform-switching implants. Int J Periodontics Restorative Dent 28 (2008): 347-355.
- Canullo L, Fedele GR, Iannello G, et al. Platform switching and marginal bone-level alterations: the results of a randomized-controlled trial. Clin Oral Implants Res 21 (2010): 115-121.
- Gardner DM. Platform switching as a means to achieving implant esthetics. N Y State Dent J 71 (2005): 34-37.
- Canullo L, Iurlaro G, Iannello G. Double-blind randomized controlled trial study on post-extraction immediately restored implants using the switching platform concept: soft tissue response. Preliminary report. Clin Oral Implants Res 20 (2009): 414-420.
- Isidor F. Loss of osseointegration caused by occlusal load of oral implants: a clinical and radiographic study in monkeys. Clin Oral Implants Res 7 (1996): 143-152.
- Qian L, Todo M, Matsushita Y, et al. Effects of implant diameter, insertion depth, and loading angle on stress/strain fields in implant/ jawbone systems: finite element analysis. Int J Oral Maxillofac Implants 24 (2009): 866-877.
- Lim TJ, Csillag A, Irinakis T, et al. Intentional angulation of an implant avoid a pneumatized maxillary sinus: a case report. J Can Dent Assoc 70 (2004): 164-168.
- Saab XE, Griggs JA, Powers JM, et al. Effect of abutment angulation on the strain on the bone around an implant in the anterior maxilla: a finite element study. J Prosthet Dent 97 (2007): 85-92.
- Ring ME. A thousand years of dental implants: a definitive history – part 2. Compend. Contin. Educ. Dent. 16 (1995).
- Albrektsson T, Brånemark PI, Hansson HA, et al. Osseointegrated titanium implants. Requirements for ensuring a long-lasting, direct bone-to-implant anchorage in man. ActaOrthopaedicaScandinavica 52 (1981): 155-170.
- Shen WL, Chen CS, Hsu ML. Influence of implant collar design on stress and strain distribution in the crestal compact bone: a three-dimensional finite element analysis. Int J Oral Maxillofac Implants 25 (2010): 901-910.
- Geng JP, Tan KB, Liu GR. Application of finite element analysis in implant dentistry: a review of the literature. J Prosthet Dent 85 (2001): 585-598.
- Assunção WG, Barão VA, Tabata LF, et al. Biomechanics studies in dentistry: bioengineering applied in oral implantology. J Craniofac Surg 20 (2009): 1173-1177.
- Srinivasan M, Padmanabhan TV. Intrusion in implant-tooth-supported fixed prosthesis: an in vitro photoelastic stress analysis. Indian J Dent Res 19 (2008): 6-11.
- Rieger MR, Fareed K, Adams WK, et al. Bone stress distribution for three endosseous implants. J Prosthet Dent 61 (1989): 223-228.
- DeTolla DH, Andreana S, Patra A, et al. Role of the finite element model in dental implants. J Oral Implantol 26 (2000): 77-81.
- Georgiopoulos B, Kalioras K, Provatidis C, et al. The effects of implant length and diameter prior to and after osseointegration: a 2-D finite element analysis. J Oral Implantol 33 (2007): 243-256.
- Juodzbalys G, Kubilius R, Eidukynas V, et al. Stress distribution in bone: single-unit implant prostheses veneered with porcelain or a new composite material. Implant Dent 14 (2005): 166-175.
- Meriç G, Erkmen E, Kurt A, et al. Biomechanical comparison of two different collar structured implants supporting 3-unit fixed partial denture: a 3-D FEM study. ActaOdontol Scand 70 (2012): 61-71.
- Erkmen E, Meriç G, Kurt A, et al. A Biomechanical comparison of implant retained fixed partial dentures with fiber reinforced composite versus conventional metal frameworks: a 3D FEA study. J MechBehav Biomed Mater 4 (2011): 107-116.
- Turner MJ, Clough RW, MactinandL HC, et al. Stiffness and defection analysis of complex structure. J. aeronaut science 23 (1956): 805-823.
- Konda P, Tarannum SA. Basic principles of finite element method and its applications in orthodontics. JPBMS 16 (2012).
- Rahmati S, Kheirollahi H, Azari A . Design and Analysis of a New Dental Implant using Finite Element Method. International Journal Of Advanced Design And Manufacturing Technology 6 (2014): 23-32.
- Cavallaro J, Greenstein G. Angled implant abutments: a practical application of available knowledge. J Am Dent Assoc 142 (2011): 142: 150-158.
- Manoj S, Krishna Prasad D, Sangeetha UN. Platform Switching?: A New Era in Implant Dentistry. 1 (2010): 61-65.
- Holmgren EP, Seckinger RJ, Kilgren LM et al. Evaluating parameters of osseointegrated dental implants using finite element analysis--a two-dimensional comparative study examining the effects of implant diameter, implant shape, and load direction. J Oral Implantol. 24 (1998):8-80.
- Martini AP, Freitas AC, Rocha EP, et al. Straight and angulated abutments in platform switching: influence of loading on bone stress by three-dimensional finite element analysis. J Craniofac Surg. 23 (2012): 8-415. doi:10.1097/SCS.0b013e31824b9c17
- Bahuguna R, Anand B, Kumar D, et al. Evaluation of stress patterns in bone around dental implant for different abutment angulations under axial and oblique loading: A finite element analysis. Natl J Maxillofac Surg. 4 (2013): 46-51.
- Li J, Li H, Shi L, et al. A mathematical model for simulating the bone remodeling process under mechanical stimulus. Dent Mater 23 (2007): 1073-1078.
- Schaeffer A. Behavior of the axis of human incisor teeth during growth. Angle Orthod 19 (1949): 254-275.
- Clelland NL, Lee JK, Bimbenet OC, et al. A three-dimensional finite element stress analysis of angled abutments for an implant placed in the anterior maxilla. J Prosthodont 4 (1995): 95-100.
- Clelland NL, Gilat A. The effect of abutment angulation on stress transfer for an implant. J Prosthodont 1 (1992): 24-28.
- Clelland NL, Gilat A, McGlumphy EA, et al. A photoelastic and strain gauge analysis of angled abutments for an implant system.Int J Oral Maxillofac Implants 8 (1993): 541-548.
- Brosh T, Pilo R, Sudai D. The influence of abutment angulation on strains and stresses along the implant/bone interface:Compari- son between two experimental techniques. J Prosthet Dent 79 (1998): 328-334.
- Caglar A, Bal BT, Aydin C, et al. Evaluation of stress occurring on three different zirconium dental implants: three-dimensional finite element analysis. Int J Oral Maxillofac Implants 25 (2010): 95-103.
- Schrotenboer Jason, Yi-Pin Tsao, Vipul Kinariwala, et al.. “Effect of Microthreads and Platform Switching on Crestal Bone Stress Levels: A Finite Element Analysis.” Journal of periodontology 79 (2008): 2166-2172. http://www.ncbi.nlm.nih.gov/pubmed/18980526 (June 28, 2014)
- Pessoa, Roberto S et al.. “Biomechanical Evaluation of Platform Switching in Different Implant Protocols: Computed Tomography-Based Three-Dimensional Finite Element Analysis.” The International journal of oral & maxillofacial implants 25(2010): 911–919. http://www.ncbi.nlm.nih.gov/pubmed/20862404.
- Okumura N, Stegaroiu R, Kitamura E, et al. Influence of maxillary cortical bone thickness, implant design and implant diameter on stress around implants: a three-dimensional finite element analysis. J Prosthodont Res 54 (2010): 133-142.
- Dejak B, Mlotkowski A. Three-dimensional finite element analysis of strength and adhesion of composite resin versus ceramic inlays in molars. J Prosthet Dent 99 (2008): 131-140.
- Bayraktar HH, Morgana EF, Nieburb GL, et al. Comparison of the elas- tic and yield properties of human femoral trabecular and cortical bone tissue. J Biomech 37 (2004): 27-35.
- Li J, Li H, Shi L, et al. A mathematical model for simulating the bone remodeling process under mechanical stimulus. Dent Mater 23 (2007): 1073-1078.
- Kerner J, Huiskes R, van Lenthe GH, et al. Correlation between pre-opera- tiveperiprosthetic bone density and post- operative bone loss in THA can be explained by strain-adaptive remodeling. J Biomech. 32 (1999) 695-703.


 Impact Factor: * 5.3
Impact Factor: * 5.3 Acceptance Rate: 75.63%
Acceptance Rate: 75.63%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 
